Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 105246 by moonanddolldoll last updated on 27/Jul/20

lim_(x→0) (cosx)^(1/x^2 )

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\mathrm{cos}{x}\right)^{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} \\ $$

Answered by bemath last updated on 27/Jul/20

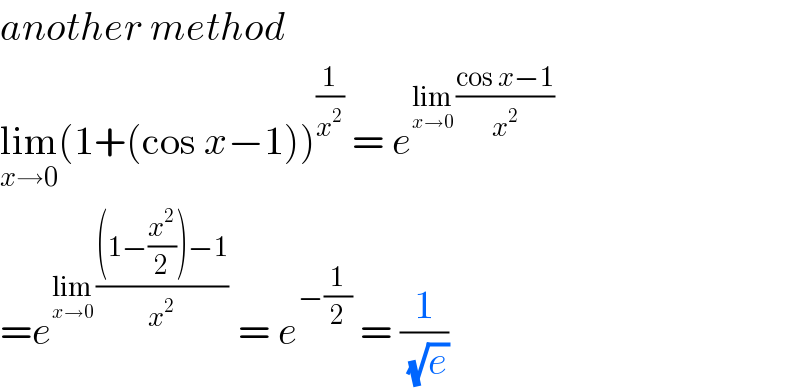
another method lim_(x→0) (1+(cos x−1))^(1/x^2 ) = e^(lim_(x→0) ((cos x−1)/x^2 )) =e^(lim_(x→0) (((1−(x^2 /2))−1)/x^2 )) = e^(−(1/2)) = (1/(√e))

$${another}\:{method} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{1}+\left(\mathrm{cos}\:{x}−\mathrm{1}\right)\right)^{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} \:=\:{e}^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{cos}\:{x}−\mathrm{1}}{{x}^{\mathrm{2}} }} \\ $$$$={e}^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)−\mathrm{1}}{{x}^{\mathrm{2}} }} \:=\:{e}^{−\frac{\mathrm{1}}{\mathrm{2}}} \:=\:\frac{\mathrm{1}}{\sqrt{{e}}}\: \\ $$

Commented by moonanddolldoll last updated on 27/Jul/20

thanks!

$${thanks}! \\ $$

Answered by bemath last updated on 27/Jul/20

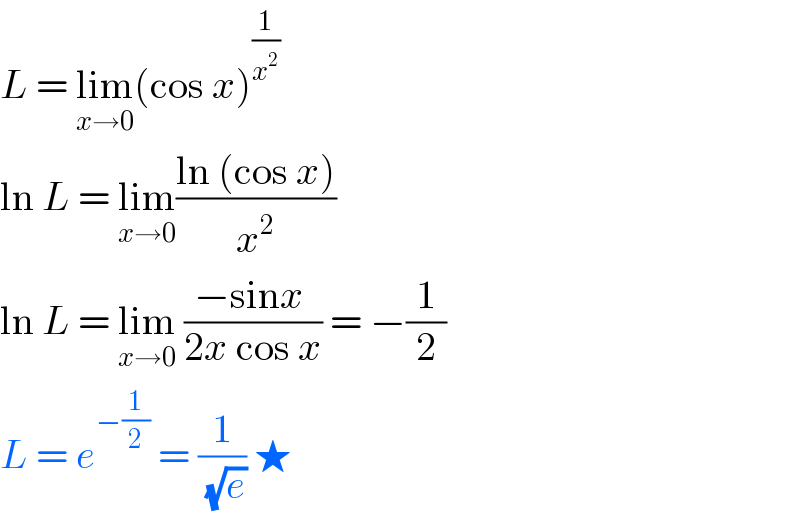
L = lim_(x→0) (cos x)^(1/x^2 ) ln L = lim_(x→0) ((ln (cos x))/x^2 ) ln L = lim_(x→0) ((−sinx )/(2x cos x)) = −(1/2) L = e^(−(1/2)) = (1/(√e)) ★

$${L}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{cos}\:{x}\right)^{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} \\ $$$$\mathrm{ln}\:{L}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{ln}\:\left(\mathrm{cos}\:{x}\right)}{{x}^{\mathrm{2}} } \\ $$$$\mathrm{ln}\:{L}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{sin}{x}\:}{\mathrm{2}{x}\:\mathrm{cos}\:{x}}\:=\:−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${L}\:=\:{e}^{−\frac{\mathrm{1}}{\mathrm{2}}} \:=\:\frac{\mathrm{1}}{\sqrt{{e}}}\:\bigstar \\ $$

Answered by abdomathmax last updated on 27/Jul/20

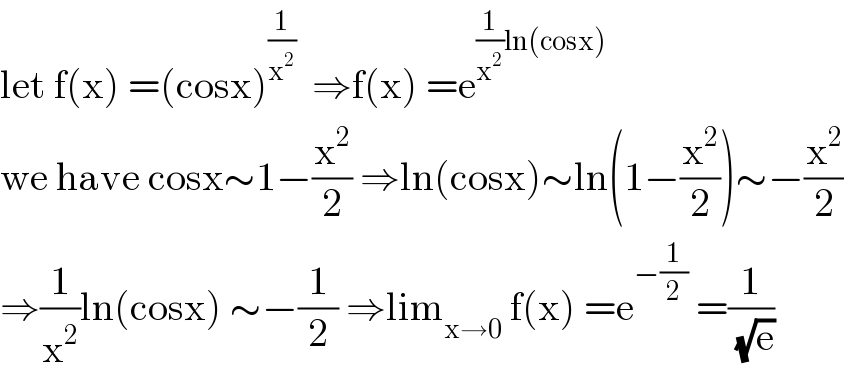
let f(x) =(cosx)^(1/x^2 ) ⇒f(x) =e^((1/x^2 )ln(cosx)) we have cosx∼1−(x^2 /2) ⇒ln(cosx)∼ln(1−(x^2 /2))∼−(x^2 /2) ⇒(1/x^2 )ln(cosx) ∼−(1/2) ⇒lim_(x→0) f(x) =e^(−(1/2)) =(1/(√e))

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\left(\mathrm{cosx}\right)^{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }} \:\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\mathrm{ln}\left(\mathrm{cosx}\right)} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{cosx}\sim\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow\mathrm{ln}\left(\mathrm{cosx}\right)\sim\mathrm{ln}\left(\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\right)\sim−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\mathrm{ln}\left(\mathrm{cosx}\right)\:\sim−\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{2}}} \:=\frac{\mathrm{1}}{\sqrt{\mathrm{e}}} \\ $$

Answered by Dwaipayan Shikari last updated on 27/Jul/20

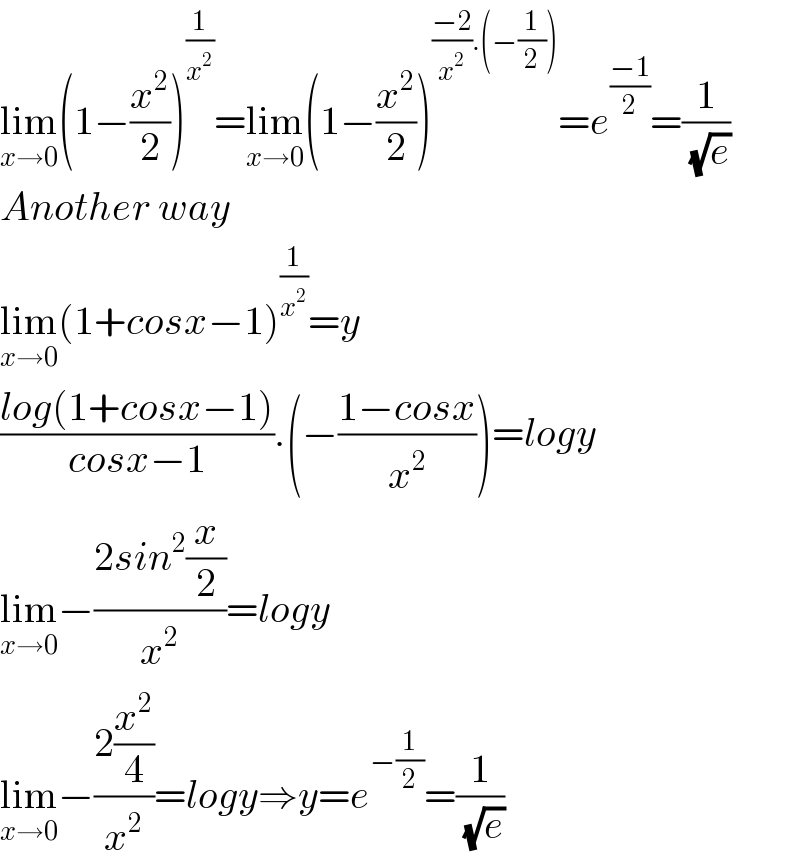
lim_(x→0) (1−(x^2 /2))^(1/x^2 ) =lim_(x→0) (1−(x^2 /2))^(((−2)/x^2 ).(−(1/2))) =e^((−1)/2) =(1/(√e)) Another way lim_(x→0) (1+cosx−1)^(1/x^2 ) =y ((log(1+cosx−1))/(cosx−1)).(−((1−cosx)/x^2 ))=logy lim_(x→0) −((2sin^2 (x/2))/x^2 )=logy lim_(x→0) −((2(x^2 /4))/x^2 )=logy⇒y=e^(−(1/2)) =(1/(√e))

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)^{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} =\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)^{\frac{−\mathrm{2}}{{x}^{\mathrm{2}} }.\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)} ={e}^{\frac{−\mathrm{1}}{\mathrm{2}}} =\frac{\mathrm{1}}{\sqrt{{e}}} \\ $$$${Another}\:{way} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{1}+{cosx}−\mathrm{1}\right)^{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} ={y} \\ $$$$\frac{{log}\left(\mathrm{1}+{cosx}−\mathrm{1}\right)}{{cosx}−\mathrm{1}}.\left(−\frac{\mathrm{1}−{cosx}}{{x}^{\mathrm{2}} }\right)={logy} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}−\frac{\mathrm{2}{sin}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{{x}^{\mathrm{2}} }={logy} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}−\frac{\mathrm{2}\frac{{x}^{\mathrm{2}} }{\mathrm{4}}}{{x}^{\mathrm{2}} }={logy}\Rightarrow{y}={e}^{−\frac{\mathrm{1}}{\mathrm{2}}} =\frac{\mathrm{1}}{\sqrt{{e}}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com