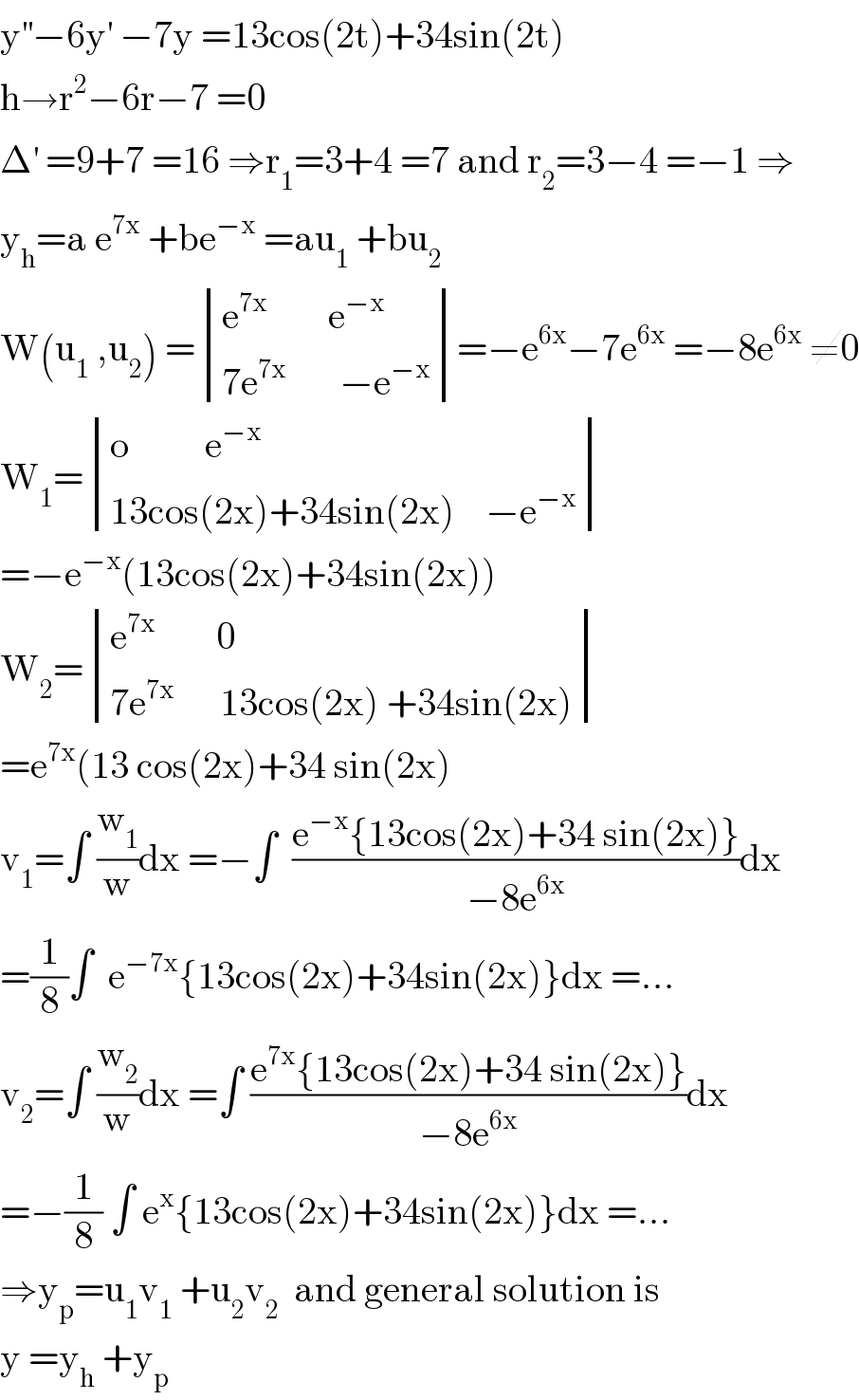Question and Answers Forum
Question Number 105266 by mohammad17 last updated on 27/Jul/20

Answered by mathmax by abdo last updated on 27/Jul/20
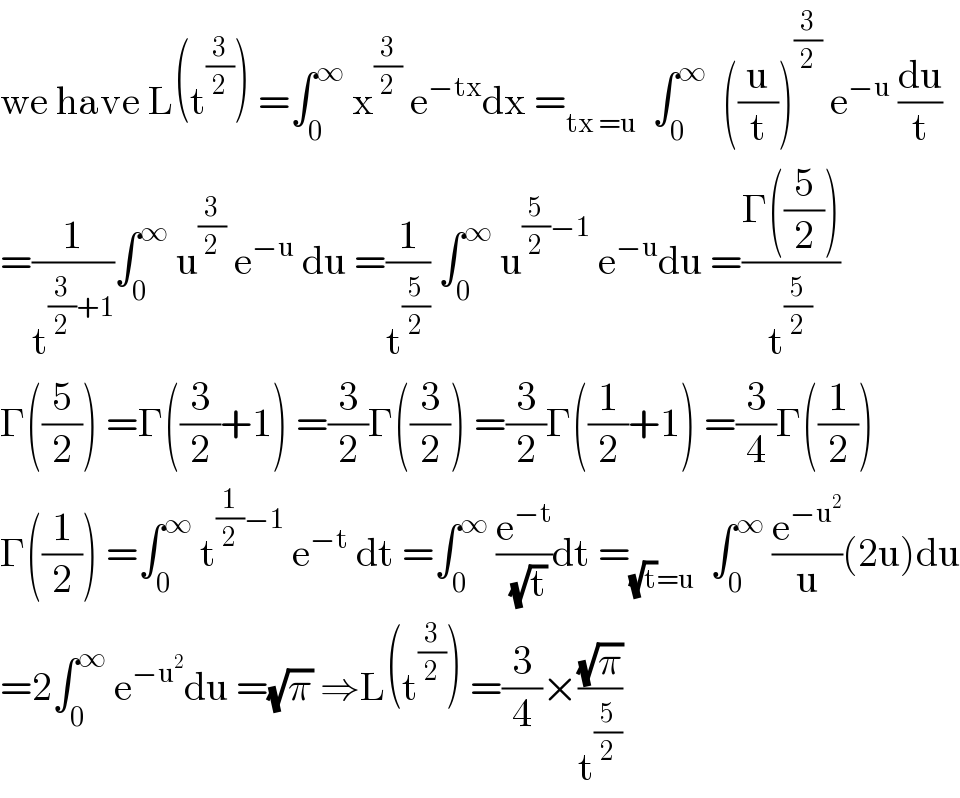
Answered by abdomathmax last updated on 27/Jul/20
![L(h(s))=∫_0 ^∞ t^2 sin(2t)e^(−st) dt =Im(∫_0 ^∞ t^2 e^(2it−st) dt) =Im(∫_0 ^∞ t^2 e^((2i−s)t) dt) but by parts ∫_0 ^∞ t^2 e^((2i−s)t) dt =[(t^2 /(2i−s))e^((2i−s)t) ]_(t=0) ^∞ −∫_0 ^∞ 2t .(1/(2i−s))e^((2i−s)t) dt =−(2/(2i−s))∫_0 ^∞ t e^((2i−s)t) dt =((−2)/(2i−s)){ [(t/(2i−s)) e^((2i−s)t) ]_0 ^∞ −∫_0 ^∞ (1/(2i−s))e^((2i−s)t) dt} =(2/((2i−s)^2 ))∫_0 ^∞ e^((2i−s)t) dt =(2/((2i−s)^2 ))[(1/(2i−s))e^((2i−s)t) ]_0 ^∞ =−(2/((2i−s)^3 )) =(2/((s−2i)^3 )) =((2(s+2i)^3 )/((s^2 +4)^3 )) =((2(s^3 +3s^2 (2i) +3s(2i)^2 +(2i)^3 ))/((s^2 +4)^3 )) =((2(s^(3 ) +6is^2 −12s−8i))/((s^2 +4)^3 )) ⇒ Im(...) =((2(6s^2 −8))/((s^2 +4)^3 )) ⇒ F(s) =((4(3s^2 −4))/((s^2 +4)^3 ))](Q105311.png)
Answered by Aziztisffola last updated on 27/Jul/20
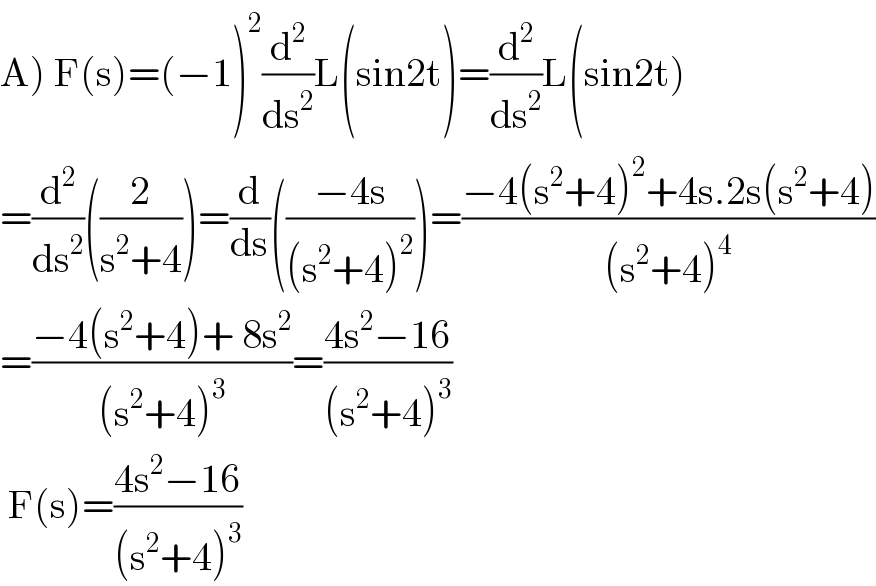
Answered by bemath last updated on 27/Jul/20
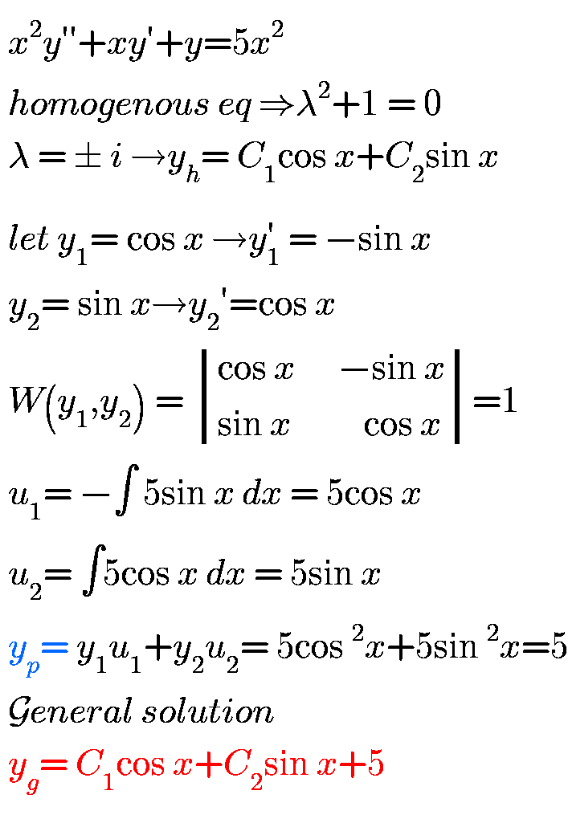
Answered by Aziztisffola last updated on 27/Jul/20
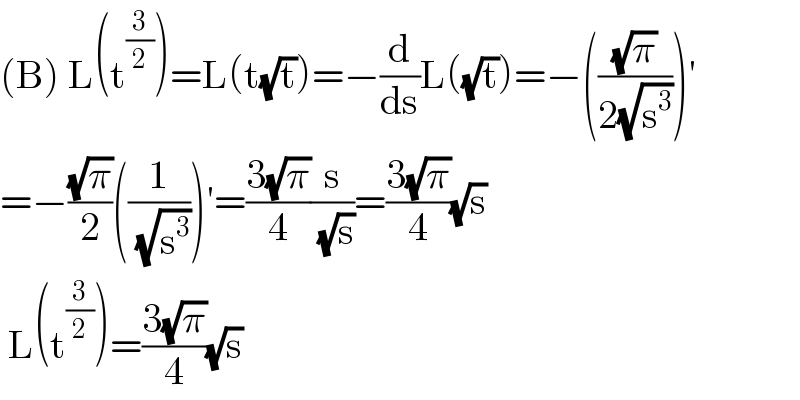
Answered by mathmax by abdo last updated on 27/Jul/20
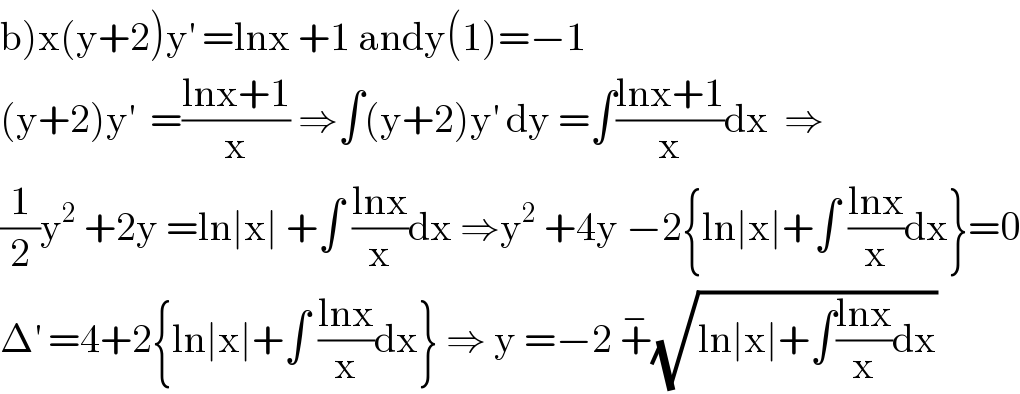
Commented by abdomathmax last updated on 27/Jul/20
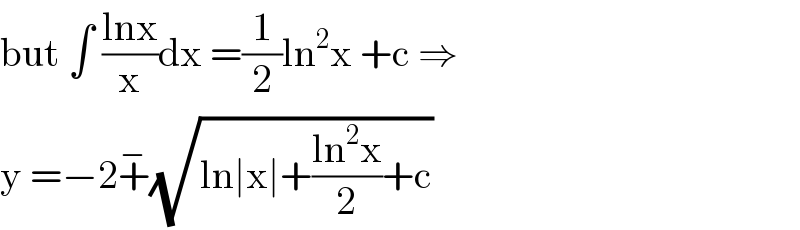
Answered by Aziztisffola last updated on 27/Jul/20
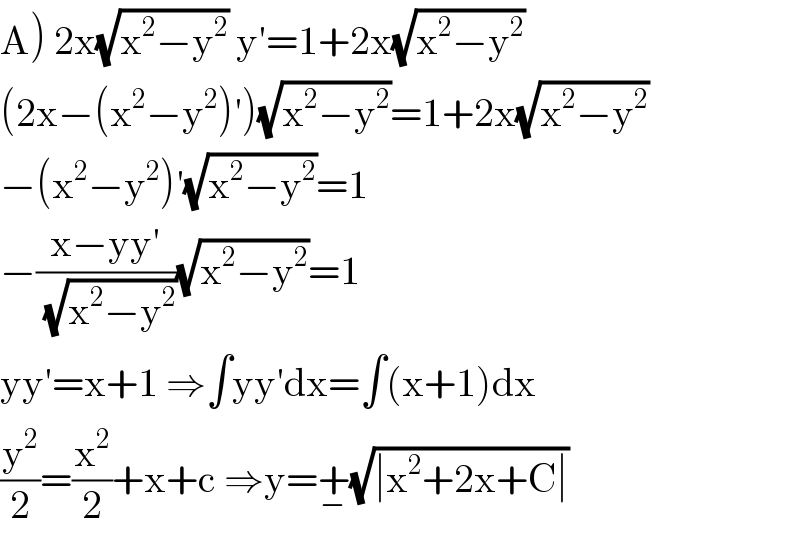
Answered by Aziztisffola last updated on 27/Jul/20
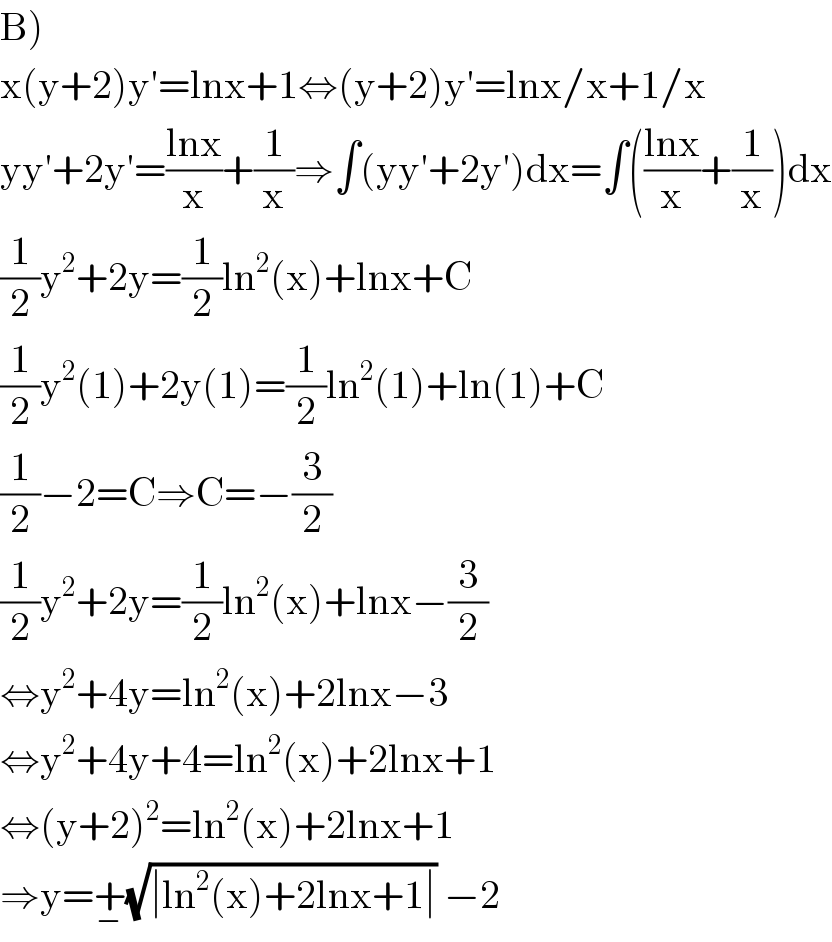
Answered by abdomathmax last updated on 27/Jul/20