Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 105283 by bemath last updated on 27/Jul/20

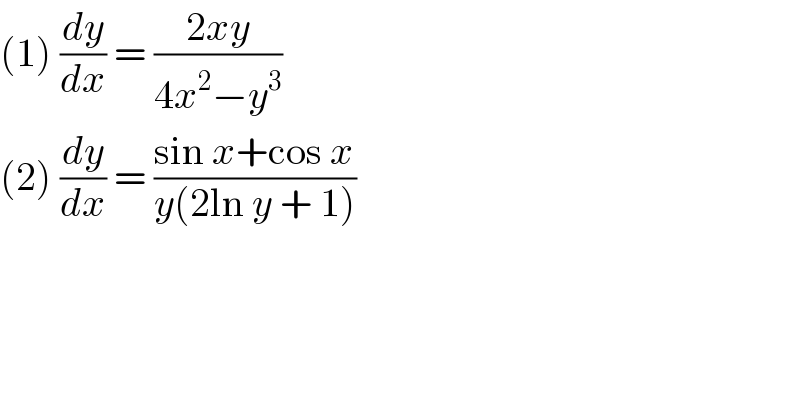
(1) (dy/dx) = ((2xy)/(4x^2 −y^3 )) (2) (dy/dx) = ((sin x+cos x)/(y(2ln y + 1)))

$$\left(\mathrm{1}\right)\:\frac{{dy}}{{dx}}\:=\:\frac{\mathrm{2}{xy}}{\mathrm{4}{x}^{\mathrm{2}} −{y}^{\mathrm{3}} } \\ $$$$\left(\mathrm{2}\right)\:\frac{{dy}}{{dx}}\:=\:\frac{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}{{y}\left(\mathrm{2ln}\:{y}\:+\:\mathrm{1}\right)} \\ $$

Answered by bobhans last updated on 27/Jul/20

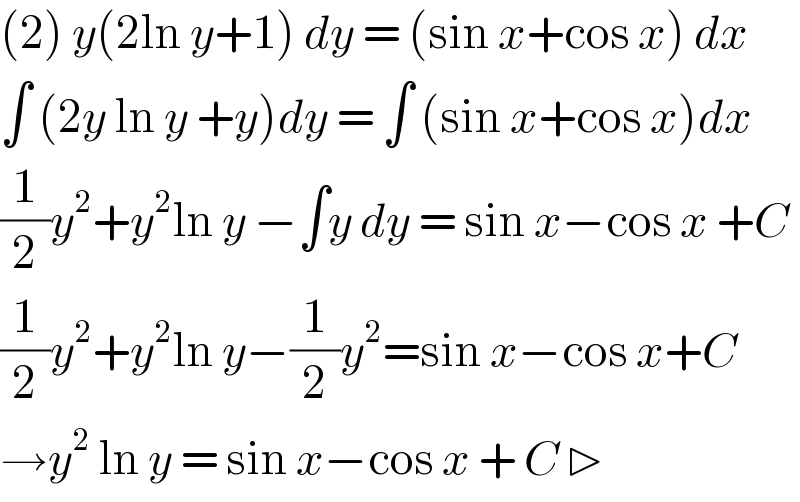
(2) y(2ln y+1) dy = (sin x+cos x) dx ∫ (2y ln y +y)dy = ∫ (sin x+cos x)dx (1/2)y^2 +y^2 ln y −∫y dy = sin x−cos x +C (1/2)y^2 +y^2 ln y−(1/2)y^2 =sin x−cos x+C →y^2 ln y = sin x−cos x + C ▷

$$\left(\mathrm{2}\right)\:{y}\left(\mathrm{2ln}\:{y}+\mathrm{1}\right)\:{dy}\:=\:\left(\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\right)\:{dx} \\ $$$$\int\:\left(\mathrm{2}{y}\:\mathrm{ln}\:{y}\:+{y}\right){dy}\:=\:\int\:\left(\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\right){dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{y}^{\mathrm{2}} +{y}^{\mathrm{2}} \mathrm{ln}\:{y}\:−\int{y}\:{dy}\:=\:\mathrm{sin}\:{x}−\mathrm{cos}\:{x}\:+{C} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{y}^{\mathrm{2}} +{y}^{\mathrm{2}} \mathrm{ln}\:{y}−\frac{\mathrm{1}}{\mathrm{2}}{y}^{\mathrm{2}} =\mathrm{sin}\:{x}−\mathrm{cos}\:{x}+{C} \\ $$$$\rightarrow{y}^{\mathrm{2}} \:\mathrm{ln}\:{y}\:=\:\mathrm{sin}\:{x}−\mathrm{cos}\:{x}\:+\:{C}\:\triangleright \\ $$

Answered by Dwaipayan Shikari last updated on 27/Jul/20

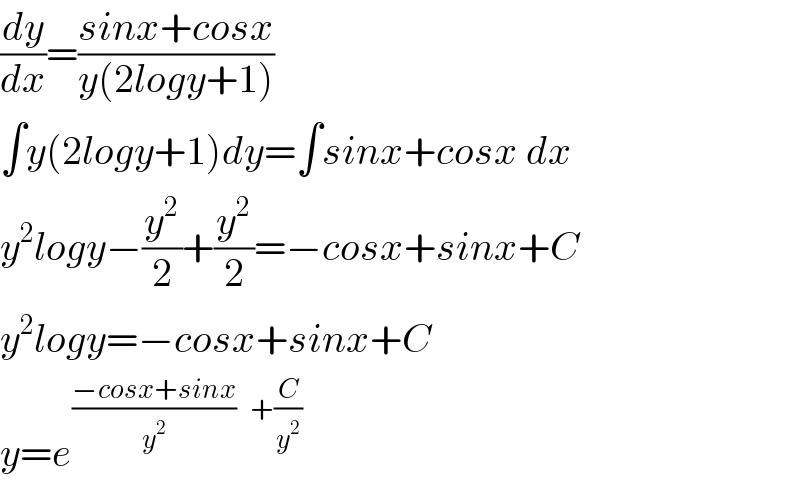
(dy/dx)=((sinx+cosx)/(y(2logy+1))) ∫y(2logy+1)dy=∫sinx+cosx dx y^2 logy−(y^2 /2)+(y^2 /2)=−cosx+sinx+C y^2 logy=−cosx+sinx+C y=e^((−cosx+sinx)/y^2 )

$$\frac{{dy}}{{dx}}=\frac{{sinx}+{cosx}}{{y}\left(\mathrm{2}{logy}+\mathrm{1}\right)} \\ $$$$\int{y}\left(\mathrm{2}{logy}+\mathrm{1}\right){dy}=\int{sinx}+{cosx}\:{dx} \\ $$$${y}^{\mathrm{2}} {logy}−\frac{{y}^{\mathrm{2}} }{\mathrm{2}}+\frac{{y}^{\mathrm{2}} }{\mathrm{2}}=−{cosx}+{sinx}+{C} \\ $$$${y}^{\mathrm{2}} {logy}=−{cosx}+{sinx}+{C} \\ $$$${y}={e}^{\frac{−{cosx}+{sinx}}{{y}^{\mathrm{2}} }} \\ $$

Answered by bobhans last updated on 27/Jul/20

(1) (y^3 −4x^2 ) dy + 2xy dx = 0 (∂N/∂x) = −8x ; (∂M/∂y) = 2x ⇔ (∂N/∂x) ≠ (∂M/∂y) non exact . by observe (((∂N/∂x)−(∂M/∂y))/M) = ((−10x)/(2xy)) = −(5/y) integrating factor u(y)=e^(∫ −(5/y) dy) u(y) = e^(−5ln y) = y^(−5) we can multiply original equation by y^(−5) ⇒(y^(−2) −4x^2 y^(−5) )dy +2xy^(−4) dx = 0 { (((∂F/∂x) = M(x,y) = 2xy^(−4) )),(((∂F/∂x) = N(x,y) = y^(−2) −4x^2 y^(−5) )) :} F(x,y) = ∫(2xy^(−4) )dx + g(y) F(x,y) = x^2 y^(−4) + g(y) ⇔g′(y) = N(x,y)−(∂/∂y) (x^2 y^(−4) ) g′(y) = y^(−2) −4x^2 y^(−5) +4x^2 y^(−5) g′(y) = y^(−2) →g(y) = ∫y^(−2) dy g(y) = −y^(−1) . Therefore we get solution ∴ x^2 y^(−4) −y^(−1) = C . ▷

$$\left(\mathrm{1}\right)\:\left({y}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{2}} \right)\:{dy}\:+\:\mathrm{2}{xy}\:{dx}\:=\:\mathrm{0} \\ $$$$\frac{\partial{N}}{\partial{x}}\:=\:−\mathrm{8}{x}\:;\:\frac{\partial{M}}{\partial{y}}\:=\:\mathrm{2}{x}\:\Leftrightarrow\:\frac{\partial{N}}{\partial{x}}\:\neq\:\frac{\partial{M}}{\partial{y}} \\ $$$${non}\:{exact}\:. \\ $$$${by}\:{observe}\:\frac{\frac{\partial{N}}{\partial{x}}−\frac{\partial{M}}{\partial{y}}}{{M}}\:=\:\frac{−\mathrm{10}{x}}{\mathrm{2}{xy}}\:=\:−\frac{\mathrm{5}}{{y}} \\ $$$${integrating}\:{factor}\:{u}\left({y}\right)={e}^{\int\:−\frac{\mathrm{5}}{{y}}\:{dy}} \\ $$$${u}\left({y}\right)\:=\:{e}^{−\mathrm{5ln}\:{y}} \:=\:{y}^{−\mathrm{5}} \\ $$$${we}\:{can}\:{multiply}\:{original}\:{equation}\:{by}\:{y}^{−\mathrm{5}} \\ $$$$\Rightarrow\left({y}^{−\mathrm{2}} −\mathrm{4}{x}^{\mathrm{2}} {y}^{−\mathrm{5}} \right){dy}\:+\mathrm{2}{xy}^{−\mathrm{4}} \:{dx}\:=\:\mathrm{0} \\ $$$$\begin{cases}{\frac{\partial{F}}{\partial{x}}\:=\:{M}\left({x},{y}\right)\:=\:\mathrm{2}{xy}^{−\mathrm{4}} }\\{\frac{\partial{F}}{\partial{x}}\:=\:{N}\left({x},{y}\right)\:=\:{y}^{−\mathrm{2}} −\mathrm{4}{x}^{\mathrm{2}} {y}^{−\mathrm{5}} }\end{cases} \\ $$$${F}\left({x},{y}\right)\:=\:\int\left(\mathrm{2}{xy}^{−\mathrm{4}} \right){dx}\:+\:{g}\left({y}\right) \\ $$$${F}\left({x},{y}\right)\:=\:{x}^{\mathrm{2}} {y}^{−\mathrm{4}} \:+\:{g}\left({y}\right) \\ $$$$\Leftrightarrow{g}'\left({y}\right)\:=\:{N}\left({x},{y}\right)−\frac{\partial}{\partial{y}}\:\left({x}^{\mathrm{2}} {y}^{−\mathrm{4}} \right) \\ $$$${g}'\left({y}\right)\:=\:{y}^{−\mathrm{2}} −\mathrm{4}{x}^{\mathrm{2}} {y}^{−\mathrm{5}} +\mathrm{4}{x}^{\mathrm{2}} {y}^{−\mathrm{5}} \\ $$$${g}'\left({y}\right)\:=\:{y}^{−\mathrm{2}} \:\rightarrow{g}\left({y}\right)\:=\:\int{y}^{−\mathrm{2}} {dy} \\ $$$${g}\left({y}\right)\:=\:−{y}^{−\mathrm{1}} .\:{Therefore}\:{we}\:{get}\:{solution} \\ $$$$\therefore\:{x}^{\mathrm{2}} {y}^{−\mathrm{4}} −{y}^{−\mathrm{1}} \:=\:{C}\:.\:\triangleright \\ $$$$ \\ $$

Commented by bemath last updated on 27/Jul/20

very...cooll thanks

$${very}...{cooll}\:{thanks}\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com