Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 105301 by Don08q last updated on 27/Jul/20

Without using tables or calculator, compare 6^7 and 7^6

$$\mathrm{Without}\:\mathrm{using}\:\mathrm{tables}\:\mathrm{or}\:\mathrm{calculator}, \\ $$$$\:{compare}\:\:\:\mathrm{6}^{\mathrm{7}} \:\mathrm{and}\:\:\:\mathrm{7}^{\mathrm{6}} \\ $$

Answered by 1549442205PVT last updated on 28/Jul/20

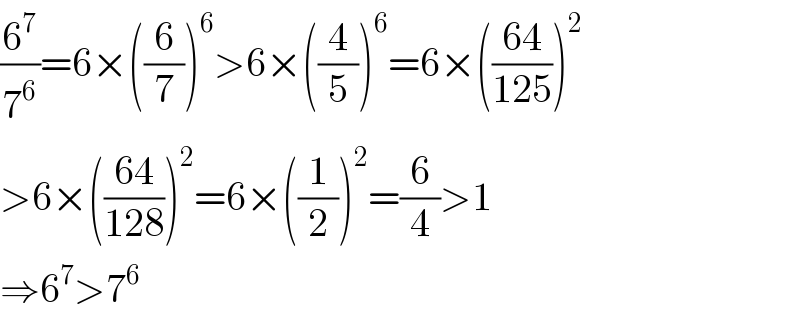
(6^7 /7^6 )=6×((6/7))^6 >6×((4/5))^6 =6×(((64)/(125)))^2 >6×(((64)/(128)))^2 =6×((1/2))^2 =(6/4)>1 ⇒6^7 >7^6

$$\frac{\mathrm{6}^{\mathrm{7}} }{\mathrm{7}^{\mathrm{6}} }=\mathrm{6}×\left(\frac{\mathrm{6}}{\mathrm{7}}\right)^{\mathrm{6}} >\mathrm{6}×\left(\frac{\mathrm{4}}{\mathrm{5}}\right)^{\mathrm{6}} =\mathrm{6}×\left(\frac{\mathrm{64}}{\mathrm{125}}\right)^{\mathrm{2}} \\ $$$$>\mathrm{6}×\left(\frac{\mathrm{64}}{\mathrm{128}}\right)^{\mathrm{2}} =\mathrm{6}×\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{\mathrm{6}}{\mathrm{4}}>\mathrm{1} \\ $$$$\Rightarrow\mathrm{6}^{\mathrm{7}} >\mathrm{7}^{\mathrm{6}} \\ $$

Commented by Don08q last updated on 28/Jul/20

Thank you Sir!

$${Thank}\:{you}\:{Sir}! \\ $$

Answered by JDamian last updated on 27/Jul/20

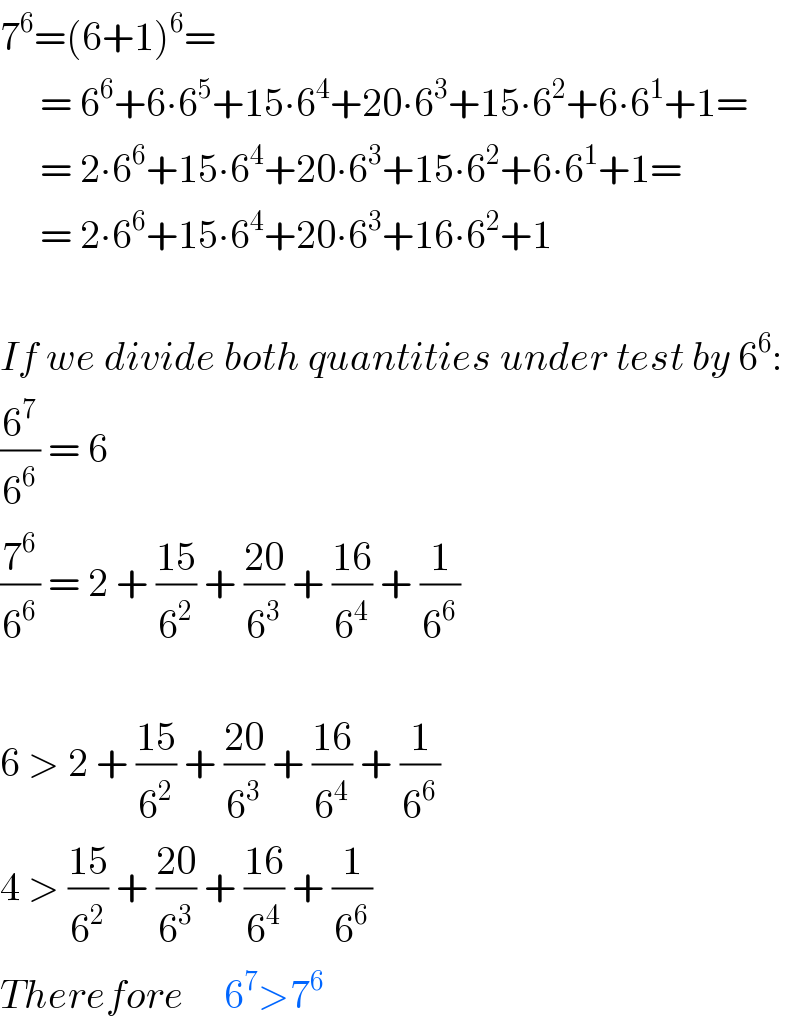
7^6 =(6+1)^6 = = 6^6 +6∙6^5 +15∙6^4 +20∙6^3 +15∙6^2 +6∙6^1 +1= = 2∙6^6 +15∙6^4 +20∙6^3 +15∙6^2 +6∙6^1 +1= = 2∙6^6 +15∙6^4 +20∙6^3 +16∙6^2 +1 If we divide both quantities under test by 6^6 : (6^7 /6^6 ) = 6 (7^6 /6^6 ) = 2 + ((15)/6^2 ) + ((20)/6^3 ) + ((16)/6^4 ) + (1/6^6 ) 6 > 2 + ((15)/6^2 ) + ((20)/6^3 ) + ((16)/6^4 ) + (1/6^6 ) 4 > ((15)/6^2 ) + ((20)/6^3 ) + ((16)/6^4 ) + (1/6^6 ) Therefore 6^7 >7^6

$$\mathrm{7}^{\mathrm{6}} =\left(\mathrm{6}+\mathrm{1}\right)^{\mathrm{6}} = \\ $$$$\:\:\:\:\:=\:\mathrm{6}^{\mathrm{6}} +\mathrm{6}\centerdot\mathrm{6}^{\mathrm{5}} +\mathrm{15}\centerdot\mathrm{6}^{\mathrm{4}} +\mathrm{20}\centerdot\mathrm{6}^{\mathrm{3}} +\mathrm{15}\centerdot\mathrm{6}^{\mathrm{2}} +\mathrm{6}\centerdot\mathrm{6}^{\mathrm{1}} +\mathrm{1}= \\ $$$$\:\:\:\:\:=\:\mathrm{2}\centerdot\mathrm{6}^{\mathrm{6}} +\mathrm{15}\centerdot\mathrm{6}^{\mathrm{4}} +\mathrm{20}\centerdot\mathrm{6}^{\mathrm{3}} +\mathrm{15}\centerdot\mathrm{6}^{\mathrm{2}} +\mathrm{6}\centerdot\mathrm{6}^{\mathrm{1}} +\mathrm{1}= \\ $$$$\:\:\:\:\:=\:\mathrm{2}\centerdot\mathrm{6}^{\mathrm{6}} +\mathrm{15}\centerdot\mathrm{6}^{\mathrm{4}} +\mathrm{20}\centerdot\mathrm{6}^{\mathrm{3}} +\mathrm{16}\centerdot\mathrm{6}^{\mathrm{2}} +\mathrm{1} \\ $$$$ \\ $$$${If}\:{we}\:{divide}\:{both}\:{quantities}\:{under}\:{test}\:{by}\:\mathrm{6}^{\mathrm{6}} : \\ $$$$\frac{\mathrm{6}^{\mathrm{7}} }{\mathrm{6}^{\mathrm{6}} }\:=\:\mathrm{6} \\ $$$$\frac{\mathrm{7}^{\mathrm{6}} }{\mathrm{6}^{\mathrm{6}} }\:=\:\mathrm{2}\:+\:\frac{\mathrm{15}}{\mathrm{6}^{\mathrm{2}} }\:+\:\frac{\mathrm{20}}{\mathrm{6}^{\mathrm{3}} }\:+\:\frac{\mathrm{16}}{\mathrm{6}^{\mathrm{4}} }\:+\:\frac{\mathrm{1}}{\mathrm{6}^{\mathrm{6}} } \\ $$$$ \\ $$$$\mathrm{6}\:>\:\mathrm{2}\:+\:\frac{\mathrm{15}}{\mathrm{6}^{\mathrm{2}} }\:+\:\frac{\mathrm{20}}{\mathrm{6}^{\mathrm{3}} }\:+\:\frac{\mathrm{16}}{\mathrm{6}^{\mathrm{4}} }\:+\:\frac{\mathrm{1}}{\mathrm{6}^{\mathrm{6}} } \\ $$$$\mathrm{4}\:>\:\frac{\mathrm{15}}{\mathrm{6}^{\mathrm{2}} }\:+\:\frac{\mathrm{20}}{\mathrm{6}^{\mathrm{3}} }\:+\:\frac{\mathrm{16}}{\mathrm{6}^{\mathrm{4}} }\:+\:\frac{\mathrm{1}}{\mathrm{6}^{\mathrm{6}} } \\ $$$${Therefore}\:\:\:\:\:\mathrm{6}^{\mathrm{7}} >\mathrm{7}^{\mathrm{6}} \\ $$

Commented by Don08q last updated on 27/Jul/20

Excellent. Thank you Sir.

$${Excellent}.\:{Thank}\:{you}\:{Sir}. \\ $$

Commented by malwaan last updated on 27/Jul/20

((15)/6^2 )<(1/2) <1 ; ((20)/6^3 )<(1/(10)) <1 ((16)/6^4 ) = (1/(81)) ≪ 1; (1/6^6 ) ≪ 1 thank you sir JDamian

$$\frac{\mathrm{15}}{\mathrm{6}^{\mathrm{2}} }<\frac{\mathrm{1}}{\mathrm{2}}\:<\mathrm{1}\:;\:\:\frac{\mathrm{20}}{\mathrm{6}^{\mathrm{3}} }<\frac{\mathrm{1}}{\mathrm{10}}\:<\mathrm{1}\: \\ $$$$\frac{\mathrm{16}}{\mathrm{6}^{\mathrm{4}} }\:=\:\frac{\mathrm{1}}{\mathrm{81}}\:\ll\:\mathrm{1};\:\frac{\mathrm{1}}{\mathrm{6}^{\mathrm{6}} }\:\ll\:\mathrm{1} \\ $$$${thank}\:{you}\:{sir}\:{JDamian} \\ $$

Answered by mathmax by abdo last updated on 27/Jul/20

for x and y naturels and x>y let compare x^y and y^x ⇒let compare ln(x^y ) and ln(y^x )(ln is increazing function..) let ϕ(x) =ylnx−xlny for y fixed we have y≥1 and x∈]y,+∞[ ϕ(y) =0 and lim_(x→+∞) ϕ(x) =lim_(x→+∞) x(y((lnx)/x)−lny) =−∞ ϕ^′ (x) =(y/x)−lny ⇒ϕ^(′′) (x) =−(y/x^2 )<0 ⇒ϕ^′ is decreazing and ϕ^′ (y) =1−lny <0 ⇒ϕ is decreazing ⇒ϕ(x)<0 ⇒ ylnx−xlny <0 ⇒ylnx<xlny ⇒x^y <y^x x=7 and y =6 x>y ⇒x^y <y^x ⇒7^6 <6^7

$$\mathrm{for}\:\mathrm{x}\:\mathrm{and}\:\mathrm{y}\:\mathrm{naturels}\:\mathrm{and}\:\mathrm{x}>\mathrm{y}\:\mathrm{let}\:\mathrm{compare}\:\mathrm{x}^{\mathrm{y}} \:\mathrm{and}\:\mathrm{y}^{\mathrm{x}} \\ $$$$\Rightarrow\mathrm{let}\:\mathrm{compare}\:\mathrm{ln}\left(\mathrm{x}^{\mathrm{y}} \right)\:\mathrm{and}\:\mathrm{ln}\left(\mathrm{y}^{\mathrm{x}} \right)\left(\mathrm{ln}\:\mathrm{is}\:\mathrm{increazing}\:\mathrm{function}..\right) \\ $$$$\left.\mathrm{let}\:\varphi\left(\mathrm{x}\right)\:=\mathrm{ylnx}−\mathrm{xlny}\:\:\:\mathrm{for}\:\mathrm{y}\:\mathrm{fixed}\:\mathrm{we}\:\mathrm{have}\:\:\mathrm{y}\geqslant\mathrm{1}\:\mathrm{and}\:\mathrm{x}\in\right]\mathrm{y},+\infty\left[\right. \\ $$$$\varphi\left(\mathrm{y}\right)\:=\mathrm{0}\:\mathrm{and}\:\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \varphi\left(\mathrm{x}\right)\:=\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{x}\left(\mathrm{y}\frac{\mathrm{lnx}}{\mathrm{x}}−\mathrm{lny}\right)\:=−\infty \\ $$$$\varphi^{'} \left(\mathrm{x}\right)\:=\frac{\mathrm{y}}{\mathrm{x}}−\mathrm{lny}\:\Rightarrow\varphi^{''} \left(\mathrm{x}\right)\:=−\frac{\mathrm{y}}{\mathrm{x}^{\mathrm{2}} }<\mathrm{0}\:\Rightarrow\varphi^{'} \:\mathrm{is}\:\mathrm{decreazing}\:\:\mathrm{and} \\ $$$$\varphi^{'} \left(\mathrm{y}\right)\:=\mathrm{1}−\mathrm{lny}\:<\mathrm{0}\:\Rightarrow\varphi\:\mathrm{is}\:\mathrm{decreazing}\:\Rightarrow\varphi\left(\mathrm{x}\right)<\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{ylnx}−\mathrm{xlny}\:<\mathrm{0}\:\Rightarrow\mathrm{ylnx}<\mathrm{xlny}\:\Rightarrow\mathrm{x}^{\mathrm{y}} <\mathrm{y}^{\mathrm{x}} \\ $$$$\mathrm{x}=\mathrm{7}\:\mathrm{and}\:\mathrm{y}\:=\mathrm{6}\:\:\mathrm{x}>\mathrm{y}\:\Rightarrow\mathrm{x}^{\mathrm{y}} <\mathrm{y}^{\mathrm{x}} \:\Rightarrow\mathrm{7}^{\mathrm{6}} <\mathrm{6}^{\mathrm{7}} \\ $$$$ \\ $$$$ \\ $$

Commented by Don08q last updated on 28/Jul/20

Thank you Sir!

$${Thank}\:{you}\:{Sir}! \\ $$

Commented by abdomsup last updated on 28/Jul/20

you are welcome

$${you}\:{are}\:{welcome} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com