Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 105370 by mohammad17 last updated on 28/Jul/20

Answered by Ar Brandon last updated on 28/Jul/20

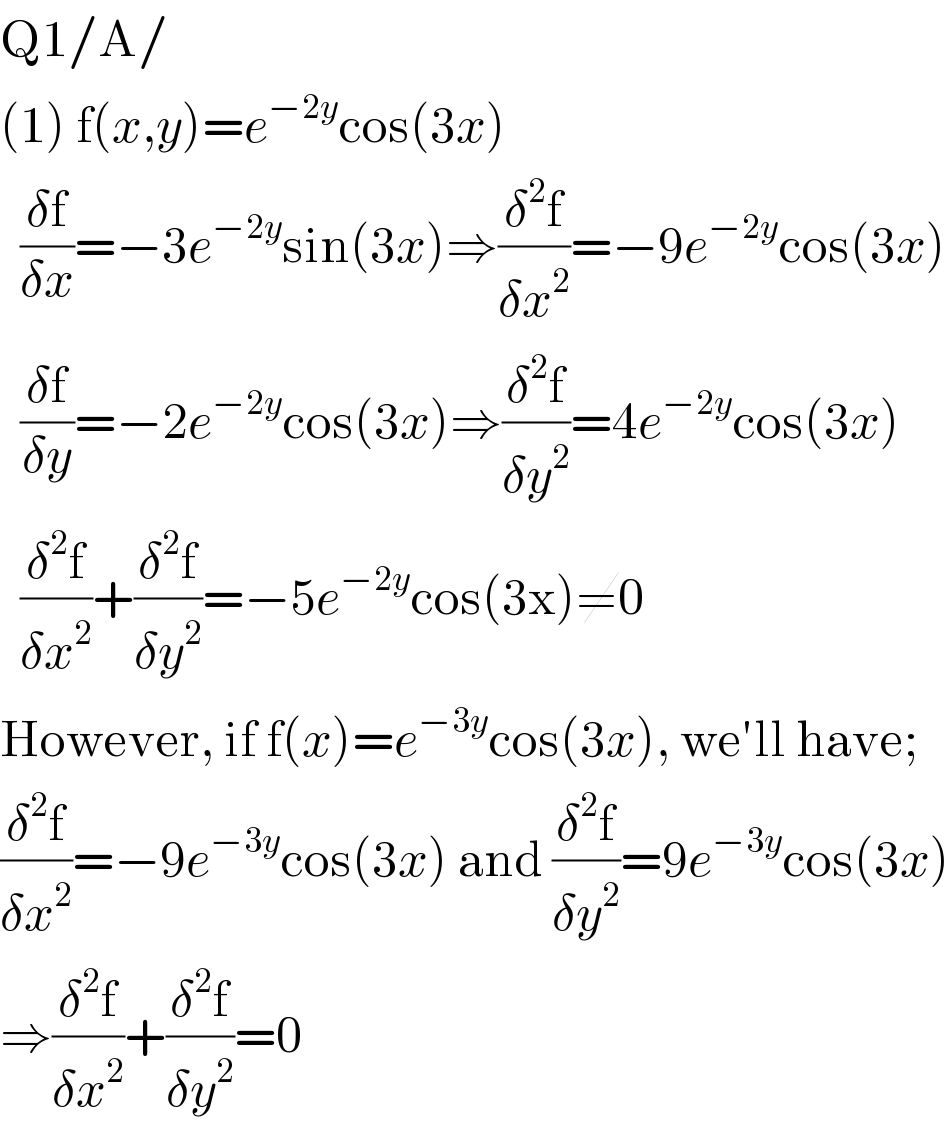
Q1/A/ (1) f(x,y)=e^(−2y) cos(3x) ((δf)/(δx))=−3e^(−2y) sin(3x)⇒((δ^2 f)/(δx^2 ))=−9e^(−2y) cos(3x) ((δf)/(δy))=−2e^(−2y) cos(3x)⇒((δ^2 f)/(δy^2 ))=4e^(−2y) cos(3x) ((δ^2 f)/(δx^2 ))+((δ^2 f)/(δy^2 ))=−5e^(−2y) cos(3x)≠0 However, if f(x)=e^(−3y) cos(3x), we′ll have; ((δ^2 f)/(δx^2 ))=−9e^(−3y) cos(3x) and ((δ^2 f)/(δy^2 ))=9e^(−3y) cos(3x) ⇒((δ^2 f)/(δx^2 ))+((δ^2 f)/(δy^2 ))=0

$$\mathrm{Q1}/\mathrm{A}/ \\ $$$$\left(\mathrm{1}\right)\:\mathrm{f}\left({x},{y}\right)={e}^{−\mathrm{2}{y}} \mathrm{cos}\left(\mathrm{3}{x}\right) \\ $$$$\:\:\frac{\delta\mathrm{f}}{\delta{x}}=−\mathrm{3}{e}^{−\mathrm{2}{y}} \mathrm{sin}\left(\mathrm{3}{x}\right)\Rightarrow\frac{\delta^{\mathrm{2}} \mathrm{f}}{\delta{x}^{\mathrm{2}} }=−\mathrm{9}{e}^{−\mathrm{2}{y}} \mathrm{cos}\left(\mathrm{3}{x}\right) \\ $$$$\:\:\frac{\delta\mathrm{f}}{\delta{y}}=−\mathrm{2}{e}^{−\mathrm{2}{y}} \mathrm{cos}\left(\mathrm{3}{x}\right)\Rightarrow\frac{\delta^{\mathrm{2}} \mathrm{f}}{\delta{y}^{\mathrm{2}} }=\mathrm{4}{e}^{−\mathrm{2}{y}} \mathrm{cos}\left(\mathrm{3}{x}\right) \\ $$$$\:\:\frac{\delta^{\mathrm{2}} \mathrm{f}}{\delta{x}^{\mathrm{2}} }+\frac{\delta^{\mathrm{2}} \mathrm{f}}{\delta{y}^{\mathrm{2}} }=−\mathrm{5}{e}^{−\mathrm{2}{y}} \mathrm{cos}\left(\mathrm{3x}\right)\neq\mathrm{0} \\ $$$$\mathrm{However},\:\mathrm{if}\:\mathrm{f}\left({x}\right)={e}^{−\mathrm{3}{y}} \mathrm{cos}\left(\mathrm{3}{x}\right),\:\mathrm{we}'\mathrm{ll}\:\mathrm{have}; \\ $$$$\frac{\delta^{\mathrm{2}} \mathrm{f}}{\delta{x}^{\mathrm{2}} }=−\mathrm{9}{e}^{−\mathrm{3}{y}} \mathrm{cos}\left(\mathrm{3}{x}\right)\:\mathrm{and}\:\frac{\delta^{\mathrm{2}} \mathrm{f}}{\delta{y}^{\mathrm{2}} }=\mathrm{9}{e}^{−\mathrm{3}{y}} \mathrm{cos}\left(\mathrm{3}{x}\right) \\ $$$$\Rightarrow\frac{\delta^{\mathrm{2}} \mathrm{f}}{\delta{x}^{\mathrm{2}} }+\frac{\delta^{\mathrm{2}} \mathrm{f}}{\delta{y}^{\mathrm{2}} }=\mathrm{0} \\ $$

Commented by mohammad17 last updated on 28/Jul/20

thank you sir

$${thank}\:{you}\:{sir} \\ $$

Answered by Dwaipayan Shikari last updated on 28/Jul/20

∫_0 ^(log2) ∫_1 ^(log4) e^(2x+y) dydx ∫_0 ^(log2) e^(2x) [e^y ]_1 ^(log4) (4−e)∫_0 ^(log2) e^(2x) dx ((4−e)/2)[e^(2x) ]_0 ^(log2) =((4−e)/2)(4−1)=(3/2)(4−e)

$$\int_{\mathrm{0}} ^{{log}\mathrm{2}} \int_{\mathrm{1}} ^{{log}\mathrm{4}} {e}^{\mathrm{2}{x}+{y}} {dydx} \\ $$$$\int_{\mathrm{0}} ^{{log}\mathrm{2}} {e}^{\mathrm{2}{x}} \left[{e}^{{y}} \right]_{\mathrm{1}} ^{{log}\mathrm{4}} \\ $$$$\left(\mathrm{4}−{e}\right)\int_{\mathrm{0}} ^{{log}\mathrm{2}} {e}^{\mathrm{2}{x}} {dx} \\ $$$$\frac{\mathrm{4}−{e}}{\mathrm{2}}\left[{e}^{\mathrm{2}{x}} \right]_{\mathrm{0}} ^{{log}\mathrm{2}} =\frac{\mathrm{4}−{e}}{\mathrm{2}}\left(\mathrm{4}−\mathrm{1}\right)=\frac{\mathrm{3}}{\mathrm{2}}\left(\mathrm{4}−{e}\right) \\ $$

Commented by mohammad17 last updated on 28/Jul/20

thank you sir

$${thank}\:{you}\:{sir} \\ $$

Answered by Dwaipayan Shikari last updated on 28/Jul/20

∫_1 ^2 ∫_0 ^4 ((√x)/y^3 )dxdy =∫_1 ^2 (2/(3y^3 ))[x^(3/2) ]_0 ^4 dy =∫_1 ^2 ((16)/3)y^(−3) dy =−[(8/(3y^2 ))]_1 ^2 =−(2/3)+(8/3)=2

$$\int_{\mathrm{1}} ^{\mathrm{2}} \int_{\mathrm{0}} ^{\mathrm{4}} \frac{\sqrt{{x}}}{{y}^{\mathrm{3}} }{dxdy} \\ $$$$=\int_{\mathrm{1}} ^{\mathrm{2}} \frac{\mathrm{2}}{\mathrm{3}{y}^{\mathrm{3}} }\left[{x}^{\frac{\mathrm{3}}{\mathrm{2}}} \right]_{\mathrm{0}} ^{\mathrm{4}} {dy} \\ $$$$=\int_{\mathrm{1}} ^{\mathrm{2}} \frac{\mathrm{16}}{\mathrm{3}}{y}^{−\mathrm{3}} {dy} \\ $$$$=−\left[\frac{\mathrm{8}}{\mathrm{3}{y}^{\mathrm{2}} }\right]_{\mathrm{1}} ^{\mathrm{2}} =−\frac{\mathrm{2}}{\mathrm{3}}+\frac{\mathrm{8}}{\mathrm{3}}=\mathrm{2} \\ $$

Commented by mohammad17 last updated on 28/Jul/20

thank you sir

$${thank}\:{you}\:{sir} \\ $$

Answered by Ar Brandon last updated on 28/Jul/20

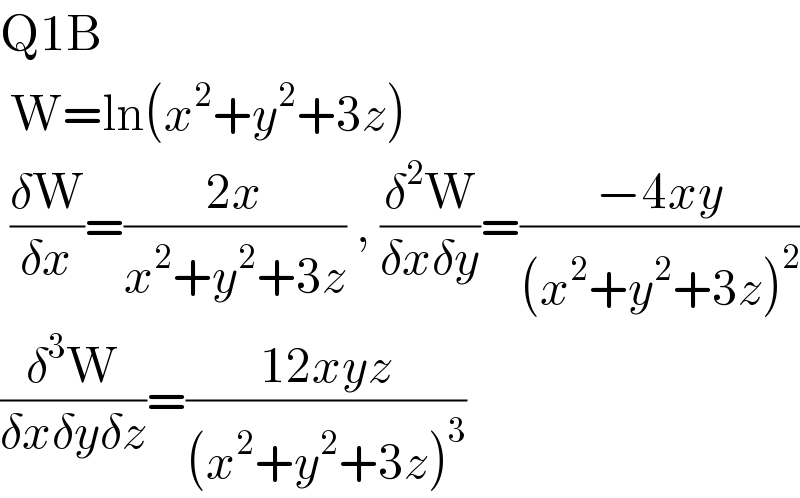
Q1B W=ln(x^2 +y^2 +3z) ((δW)/(δx))=((2x)/(x^2 +y^2 +3z)) , ((δ^2 W)/(δxδy))=((−4xy)/((x^2 +y^2 +3z)^2 )) ((δ^3 W)/(δxδyδz))=((12xyz)/((x^2 +y^2 +3z)^3 ))

$$\mathrm{Q1B} \\ $$$$\:\mathrm{W}=\mathrm{ln}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{3}{z}\right) \\ $$$$\:\frac{\delta\mathrm{W}}{\delta{x}}=\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{3}{z}}\:,\:\frac{\delta^{\mathrm{2}} \mathrm{W}}{\delta{x}\delta{y}}=\frac{−\mathrm{4}{xy}}{\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{3}{z}\right)^{\mathrm{2}} } \\ $$$$\frac{\delta^{\mathrm{3}} \mathrm{W}}{\delta{x}\delta{y}\delta{z}}=\frac{\mathrm{12}{xyz}}{\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{3}{z}\right)^{\mathrm{3}} } \\ $$

Commented by mohammad17 last updated on 28/Jul/20

thank you sir

$${thank}\:{you}\:{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com