∫((x^2 +3)/(x^6 (x^2 +1)))dx Is there any special method of decomposition other than the use of partial fractions ?


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 105411 by Ar Brandon last updated on 28/Jul/20
$∫((x^2 +3)/(x^6 (x^2 +1)))dx Is there any special method of decomposition other than the use of partial fractions ?$
$\int \frac{x^{2} + 3}{x^{6} (x^{2} + 1)} d x$ $I s t h e r e a n y s p e c i a l m e t h o d o f d e c o m p o s i t i o n$ $o t h e r t h a n t h e u s e o f p a r t i a l f r a c t i o n s ?$
	Answered by Dwaipayan Shikari last updated on 28/Jul/20

	$\int \frac{x^{2} + 1}{x^{6} (x^{2} + 1)} + \frac{2}{x^{6} (x^{2} + 1)} d x$ $\int \frac{1}{x^{6}} + 2 \int \frac{1}{x^{4}} (\frac{1}{x^{2}} - \frac{1}{x^{2} + 1}) d x$ $3 \int \frac{1}{x^{6}} - 2 \int \frac{1}{x^{4} (x^{2} + 1)} d x$ $3 \int \frac{1}{x^{6}} - 2 \int \frac{1}{x^{2}} (\frac{1}{x^{2}} - \frac{1}{x^{2} + 1}) d x$ $3 \int \frac{1}{x^{6}} - 2 \int \frac{1}{x^{4}} + 2 \int \frac{1}{x^{2} (x^{2} + 1)} d x$ $3 \int \frac{1}{x^{6}} - 2 \int \frac{1}{x^{4}} + 2 \int \frac{1}{x^{2}} - 2 \int \frac{1}{x^{2} + 1} d x$ $- \frac{3}{5 x^{5}} + \frac{2}{3 x^{3}} - \frac{2}{x} - 2 {t a n}^{- 1} x + C$
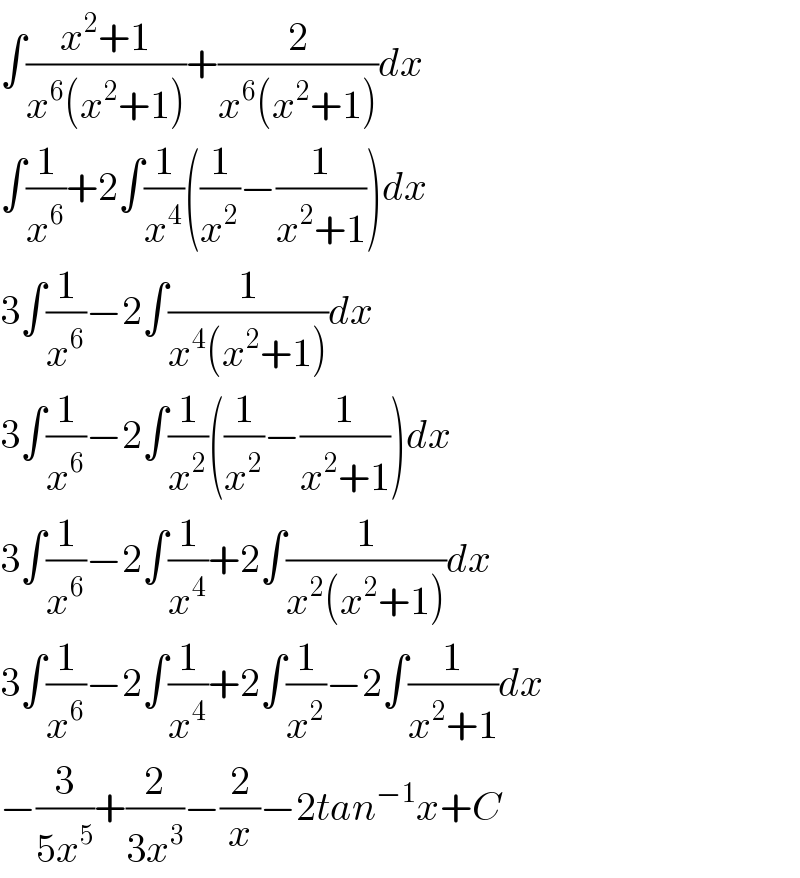
	Commented by Dwaipayan Shikari last updated on 28/Jul/20

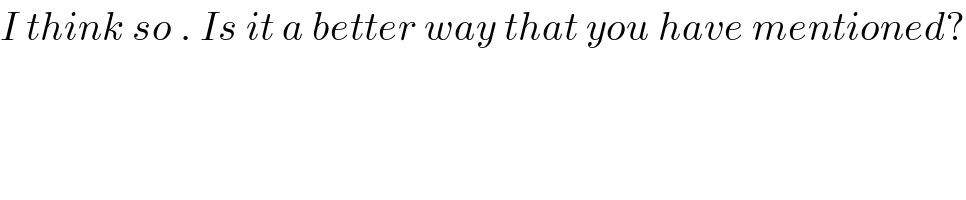
	$I t h i n k s o . I s i t a b e t t e r w a y t h a t y o u h a v e m e n t i o n e d ?$
	Commented by Dwaipayan Shikari last updated on 28/Jul/20
	��
	Commented by Ar Brandon last updated on 28/Jul/20
	Perfect, bro. Exactly what I needed. Thanks��
	Commented by Ar Brandon last updated on 28/Jul/20

	$\frac{1}{x^{2} (x^{2} + 1)} = \frac{x^{2} + 1 - x^{2}}{x^{2} (x^{2} + 1)} = \frac{x^{2} + 1}{x^{2} (x^{2} + 1)} - \frac{x^{2}}{x^{2} (x^{2} + 1)}$ $= \frac{1}{x^{2}} - \frac{1}{x^{2} + 1},$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum