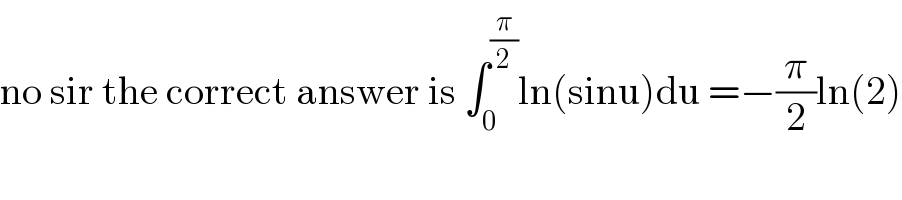Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 105412 by john santu last updated on 28/Jul/20

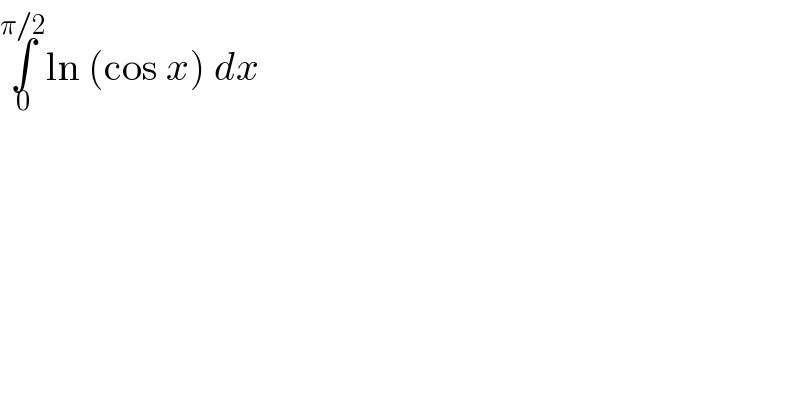
∫_0 ^(π/2) ln (cos x) dx

$$\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\mathrm{ln}\:\left(\mathrm{cos}\:{x}\right)\:{dx} \\ $$

Answered by Dwaipayan Shikari last updated on 28/Jul/20

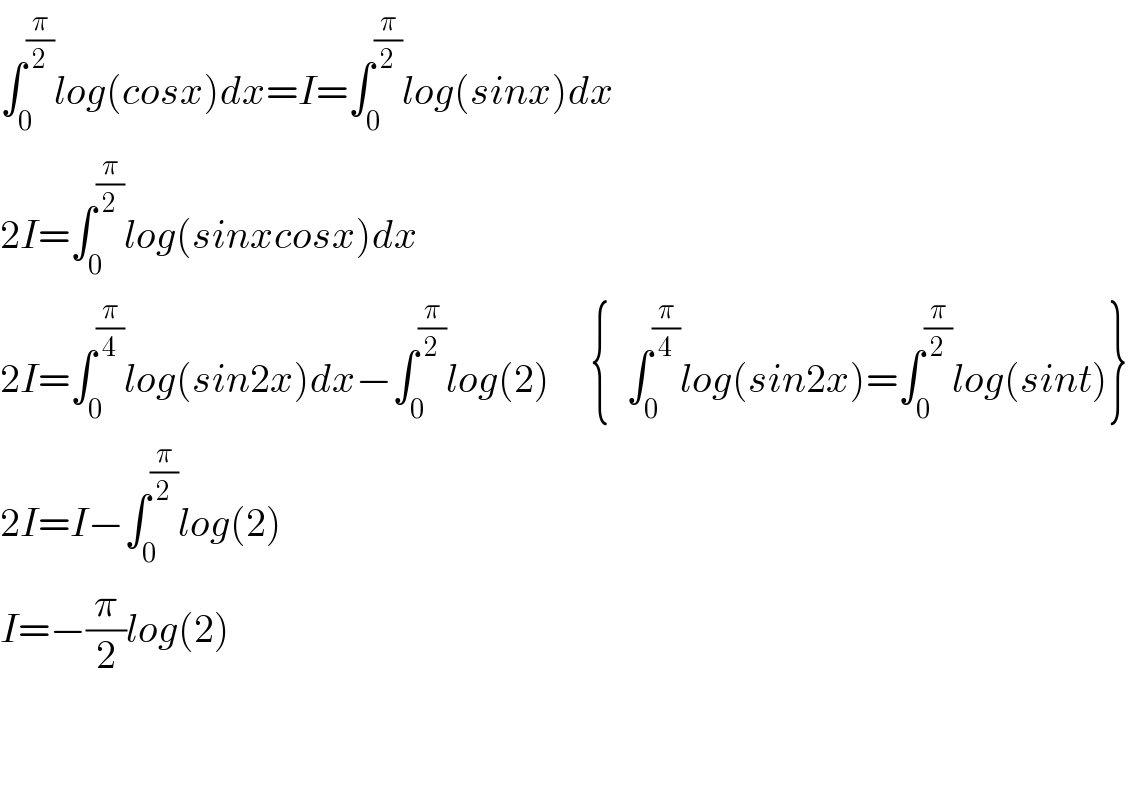
∫_0 ^(π/2) log(cosx)dx=I=∫_0 ^(π/2) log(sinx)dx 2I=∫_0 ^(π/2) log(sinxcosx)dx 2I=∫_0 ^(π/4) log(sin2x)dx−∫_0 ^(π/2) log(2) { ∫_0 ^(π/4) log(sin2x)=∫_0 ^(π/2) log(sint)} 2I=I−∫_0 ^(π/2) log(2) I=−(π/2)log(2)

$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left({cosx}\right){dx}={I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left({sinx}\right){dx} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left({sinxcosx}\right){dx} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {log}\left({sin}\mathrm{2}{x}\right){dx}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left(\mathrm{2}\right)\:\:\:\:\:\left\{\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {log}\left({sin}\mathrm{2}{x}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left({sint}\right)\right\} \\ $$$$\mathrm{2}{I}={I}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left(\mathrm{2}\right) \\ $$$${I}=−\frac{\pi}{\mathrm{2}}{log}\left(\mathrm{2}\right) \\ $$$$ \\ $$$$ \\ $$

Commented by bemath last updated on 28/Jul/20

∫_0 ^(π/2) log (2) dx ?

$$\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\mathrm{log}\:\left(\mathrm{2}\right)\:{dx}\:?\: \\ $$

Commented by Dwaipayan Shikari last updated on 28/Jul/20

[xlog(2)]_0 ^(π/2) =((π/2)−0)log2=(π/2)log2

$$\left[{xlog}\left(\mathrm{2}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} =\left(\frac{\pi}{\mathrm{2}}−\mathrm{0}\right){log}\mathrm{2}=\frac{\pi}{\mathrm{2}}{log}\mathrm{2} \\ $$

Commented by Dwaipayan Shikari last updated on 28/Jul/20

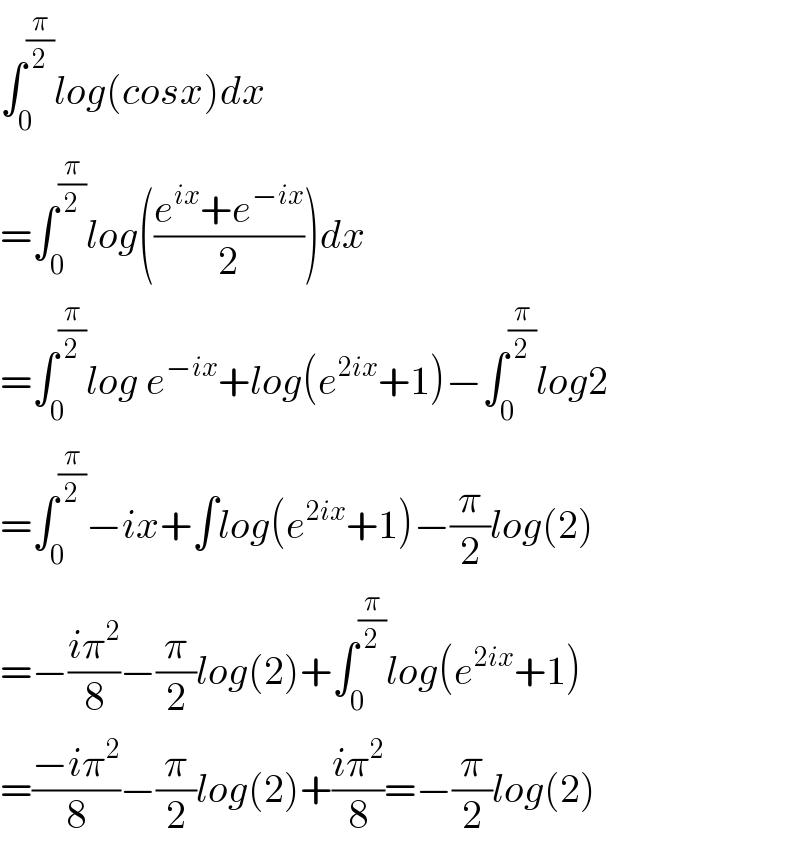
∫_0 ^(π/2) log(cosx)dx =∫_0 ^(π/2) log(((e^(ix) +e^(−ix) )/2))dx =∫_0 ^(π/2) log e^(−ix) +log(e^(2ix) +1)−∫_0 ^(π/2) log2 =∫_0 ^(π/2) −ix+∫log(e^(2ix) +1)−(π/2)log(2) =−((iπ^2 )/8)−(π/2)log(2)+∫_0 ^(π/2) log(e^(2ix) +1) =((−iπ^2 )/8)−(π/2)log(2)+((iπ^2 )/8)=−(π/2)log(2)

$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left({cosx}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left(\frac{{e}^{{ix}} +{e}^{−{ix}} }{\mathrm{2}}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\:{e}^{−{ix}} +{log}\left({e}^{\mathrm{2}{ix}} +\mathrm{1}\right)−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\mathrm{2} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} −{ix}+\int{log}\left({e}^{\mathrm{2}{ix}} +\mathrm{1}\right)−\frac{\pi}{\mathrm{2}}{log}\left(\mathrm{2}\right) \\ $$$$=−\frac{{i}\pi^{\mathrm{2}} }{\mathrm{8}}−\frac{\pi}{\mathrm{2}}{log}\left(\mathrm{2}\right)+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left({e}^{\mathrm{2}{ix}} +\mathrm{1}\right) \\ $$$$=\frac{−{i}\pi^{\mathrm{2}} }{\mathrm{8}}−\frac{\pi}{\mathrm{2}}{log}\left(\mathrm{2}\right)+\frac{{i}\pi^{\mathrm{2}} }{\mathrm{8}}=−\frac{\pi}{\mathrm{2}}{log}\left(\mathrm{2}\right) \\ $$

Commented by Dwaipayan Shikari last updated on 28/Jul/20

Commented by Dwaipayan Shikari last updated on 28/Jul/20

From wolfram alpha

$${From}\:{wolfram}\:{alpha} \\ $$

Answered by bemath last updated on 29/Jul/20

Commented by mathmax by abdo last updated on 29/Jul/20

no sir the correct answer is ∫_0 ^(π/2) ln(sinu)du =−(π/2)ln(2)

$$\mathrm{no}\:\mathrm{sir}\:\mathrm{the}\:\mathrm{correct}\:\mathrm{answer}\:\mathrm{is}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{sinu}\right)\mathrm{du}\:=−\frac{\pi}{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com