
Question Number 105431 by bachamohamed last updated on 28/Jul/20
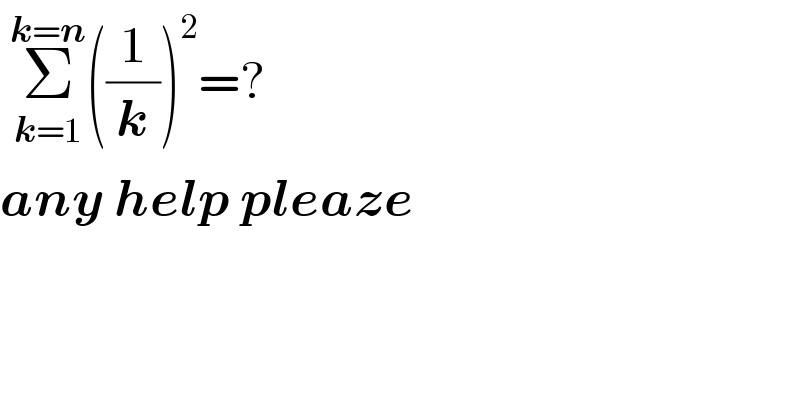
$$\:\underset{\boldsymbol{{k}}=\mathrm{1}} {\overset{\boldsymbol{{k}}=\boldsymbol{{n}}} {\sum}}\left(\frac{\mathrm{1}}{\boldsymbol{{k}}}\right)^{\mathrm{2}} =? \\ $$$$\boldsymbol{{any}}\:\boldsymbol{{help}}\:\boldsymbol{{pleaze}} \\ $$
Commented by Dwaipayan Shikari last updated on 28/Jul/20
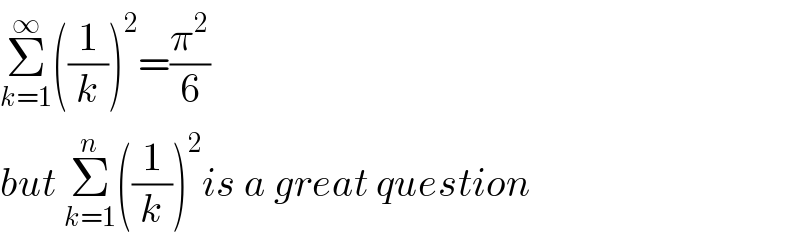
$$\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{k}}\right)^{\mathrm{2}} =\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$${but}\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\frac{\mathrm{1}}{{k}}\right)^{\mathrm{2}} {is}\:{a}\:{great}\:{question} \\ $$
Commented by bachamohamed last updated on 28/Jul/20
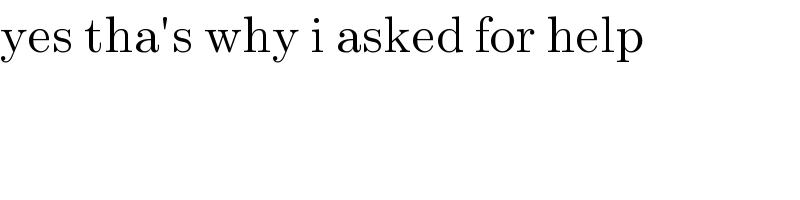
$$\mathrm{yes}\:\mathrm{tha}'\mathrm{s}\:\mathrm{why}\:\mathrm{i}\:\mathrm{asked}\:\mathrm{for}\:\mathrm{help} \\ $$
Commented by Rohit@Thakur last updated on 28/Jul/20
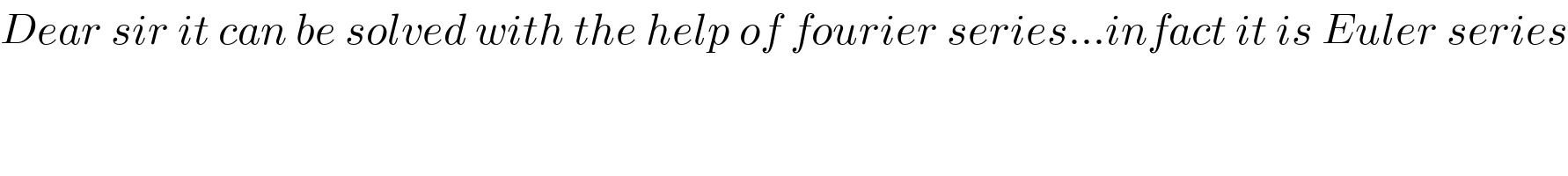
$${Dear}\:{sir}\:{it}\:{can}\:{be}\:{solved}\:{with}\:{the}\:{help}\:{of}\:{fourier}\:{series}...{infact}\:{it}\:{is}\:{Euler}\:{series} \\ $$
Commented by mathmax by abdo last updated on 28/Jul/20
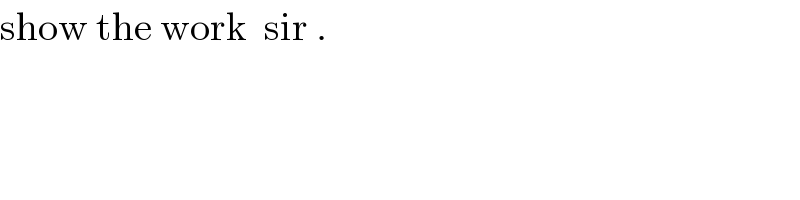
$$\mathrm{show}\:\mathrm{the}\:\mathrm{work}\:\:\mathrm{sir}\:. \\ $$
Commented by Dwaipayan Shikari last updated on 29/Jul/20

$${Cauchy}\:{schwarz}\:{inequality} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left({k}\right)^{\mathrm{2}} .\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\frac{\mathrm{1}}{{k}}\right)^{\mathrm{2}} \geqslant\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}_{} .\frac{\mathrm{1}}{{k}}\right)^{\mathrm{2}} \\ $$$$\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}}.\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\frac{\mathrm{1}}{{k}}\right)^{\mathrm{2}} \geqslant\left({n}\right)^{\mathrm{2}} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\frac{\mathrm{1}}{{k}}\right)^{\mathrm{2}} \geqslant\frac{\mathrm{6}{n}}{\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)} \\ $$$$ \\ $$$$ \\ $$
Commented by Dwaipayan Shikari last updated on 29/Jul/20
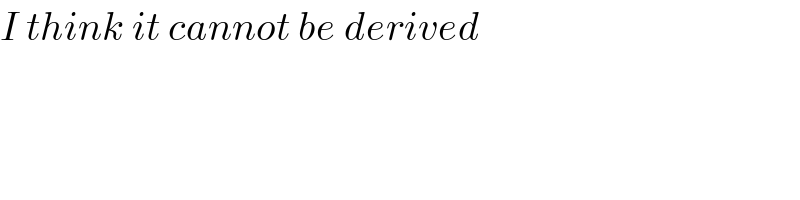
$${I}\:{think}\:{it}\:{cannot}\:{be}\:{derived} \\ $$
Answered by mathmax by abdo last updated on 28/Jul/20
![we get this sum by iteration let S_n =Σ_(k=1) ^n (1/k^2 ) ⇒ S_n =Σ_(k=2p) (1/k^2 ) +Σ_(k=2p+1) (1/k^2 ) =Σ_(p=1) ^([(n/2)]) (1/(4p^2 )) +Σ_(p=0) ^([((n−1)/2)] ) (1/((2p+1)^2 )) also Σ_(p=1) ^([(n/2)]) (1/p^2 ) =Σ_(2m≤[(n/2)]) (1/(4m^2 )) +Σ_(2m+1 ≤[(n/2)]) (1/((2m+1)^2 )) =(1/4)Σ_(m=1) ^([(([(n/2)])/2)]) (1/m^2 ) +Σ_(m=0) ^([(([(n/2)]−1)/2)]) (1/((2m+1)^2 )) =..... example Σ_(n=1) ^(10) (1/n^2 ) =Σ_(n=1) ^([((10)/2)]) (1/(4n^2 )) +Σ_(n=0) ^([(9/2)]) (1/((2n+1)^2 )) =(1/4) Σ_(n=1) ^5 (1/n^2 ) +Σ_(n=0) ^4 (1/((2n+1)^2 )) =(1/4){ Σ_(n=1) ^([(5/2)]) (1/(4n^2 )) +Σ_(n=0) ^2 (1/((2n+1)^2 ))} +Σ_(n=0) ^4 (1/((2n+1)^2 )) =(1/4^2 ) Σ_(n=1) ^2 (1/n^2 ) +((1/4)+1)Σ_(n=0) ^2 (1/((2n+1)^2 )) +Σ_(n=3) ^4 (1/((2n+1)^2 )) =(1/(16))(1+(1/4)) +(5/4)(1 +(1/9) +(1/(25))) +(1/7^2 ) +(1/9^2 ) =....](Q105443.png)
$$\mathrm{we}\:\mathrm{get}\:\mathrm{this}\:\mathrm{sum}\:\mathrm{by}\:\mathrm{iteration}\:\:\mathrm{let}\:\mathrm{S}_{\mathrm{n}} =\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{S}_{\mathrm{n}} =\sum_{\mathrm{k}=\mathrm{2p}} \:\:\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{2}} }\:+\sum_{\mathrm{k}=\mathrm{2p}+\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{2}} }\:=\sum_{\mathrm{p}=\mathrm{1}} ^{\left[\frac{\mathrm{n}}{\mathrm{2}}\right]} \:\frac{\mathrm{1}}{\mathrm{4p}^{\mathrm{2}} }\:+\sum_{\mathrm{p}=\mathrm{0}} ^{\left[\frac{\mathrm{n}−\mathrm{1}}{\mathrm{2}}\right]\:} \:\frac{\mathrm{1}}{\left(\mathrm{2p}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{also}\:\sum_{\mathrm{p}=\mathrm{1}} ^{\left[\frac{\mathrm{n}}{\mathrm{2}}\right]} \:\frac{\mathrm{1}}{\mathrm{p}^{\mathrm{2}} }\:=\sum_{\mathrm{2m}\leqslant\left[\frac{\mathrm{n}}{\mathrm{2}}\right]} \:\:\:\frac{\mathrm{1}}{\mathrm{4m}^{\mathrm{2}} }\:+\sum_{\mathrm{2m}+\mathrm{1}\:\leqslant\left[\frac{\mathrm{n}}{\mathrm{2}}\right]} \:\:\:\frac{\mathrm{1}}{\left(\mathrm{2m}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\sum_{\mathrm{m}=\mathrm{1}} ^{\left[\frac{\left[\frac{\mathrm{n}}{\mathrm{2}}\right]}{\mathrm{2}}\right]} \:\frac{\mathrm{1}}{\mathrm{m}^{\mathrm{2}} }\:+\sum_{\mathrm{m}=\mathrm{0}} ^{\left[\frac{\left[\frac{\mathrm{n}}{\mathrm{2}}\right]−\mathrm{1}}{\mathrm{2}}\right]} \:\frac{\mathrm{1}}{\left(\mathrm{2m}+\mathrm{1}\right)^{\mathrm{2}} }\:=..... \\ $$$$\mathrm{example}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\mathrm{10}} \:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\left[\frac{\mathrm{10}}{\mathrm{2}}\right]} \:\frac{\mathrm{1}}{\mathrm{4n}^{\mathrm{2}} }\:+\sum_{\mathrm{n}=\mathrm{0}} ^{\left[\frac{\mathrm{9}}{\mathrm{2}}\right]} \:\frac{\mathrm{1}}{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\mathrm{5}} \:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\:+\sum_{\mathrm{n}=\mathrm{0}} ^{\mathrm{4}} \:\frac{\mathrm{1}}{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left\{\:\sum_{\mathrm{n}=\mathrm{1}} ^{\left[\frac{\mathrm{5}}{\mathrm{2}}\right]} \:\frac{\mathrm{1}}{\mathrm{4n}^{\mathrm{2}} }\:+\sum_{\mathrm{n}=\mathrm{0}} ^{\mathrm{2}} \:\frac{\mathrm{1}}{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} }\right\}\:+\sum_{\mathrm{n}=\mathrm{0}} ^{\mathrm{4}} \:\frac{\mathrm{1}}{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{2}} }\:\sum_{\mathrm{n}=\mathrm{1}} ^{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\:\:+\left(\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{1}\right)\sum_{\mathrm{n}=\mathrm{0}} ^{\mathrm{2}} \:\frac{\mathrm{1}}{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} }\:+\sum_{\mathrm{n}=\mathrm{3}} ^{\mathrm{4}} \:\frac{\mathrm{1}}{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}\right)\:+\frac{\mathrm{5}}{\mathrm{4}}\left(\mathrm{1}\:+\frac{\mathrm{1}}{\mathrm{9}}\:+\frac{\mathrm{1}}{\mathrm{25}}\right)\:+\frac{\mathrm{1}}{\mathrm{7}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{9}^{\mathrm{2}} }\:=.... \\ $$
Commented by bachamohamed last updated on 01/Aug/20

$$\mathrm{thank}'\mathrm{s}\:\mathrm{sir} \\ $$
