Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 105440 by Ar Brandon last updated on 28/Jul/20

$$\int \mathrm{tanx}\cdot \tan 2\mathrm{x}\cdot \tan 3\mathrm{x}\cdot \mathrm{dx}$$$$\mathrm{Any}\mathrm{way}\mathrm{to}\mathrm{solve}\mathrm{this}\mathrm{without}\mathrm{the}\mathrm{use}\mathrm{of}$$$$\mathrm{partial}\mathrm{fractions}?$$

Commented by som(math1967) last updated on 29/Jul/20

$$\tan 3\mathrm{x}=\frac{\tan 2\mathrm{x}+\mathrm{tanx}}{1-\tan 2\mathrm{xtanx}}$$$$\therefore \tan 3\mathrm{x}-\tan 2\mathrm{x}-\mathrm{tanx}=\tan 3\mathrm{xtan}2\mathrm{xtanx}$$$$\therefore \int \tan 3\mathrm{xtan}2\mathrm{xtanxdx}$$$$=\int \tan 3\mathrm{xdx}-\int \tan 2\mathrm{xdx}-\int \mathrm{tanxdx}=$$$$=\frac{1}{3}\mathrm{lnsec}3\mathrm{x}+\frac{1}{2}\mathrm{lncos}2\mathrm{x}+\mathrm{lncosx}+\mathrm{C}$$

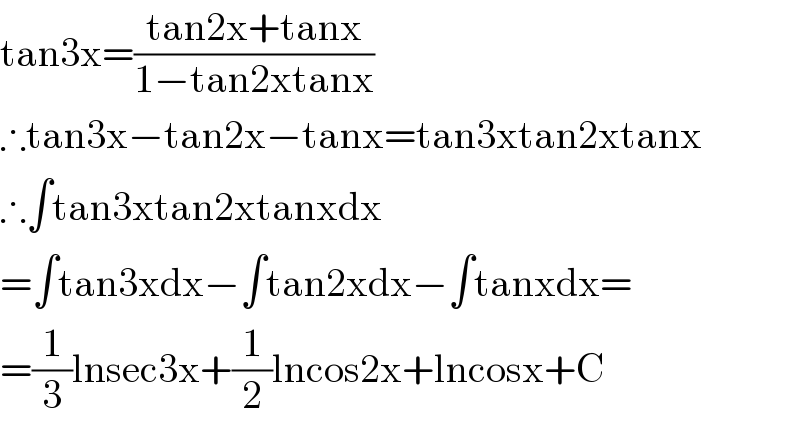
Commented by Ar Brandon last updated on 29/Jul/20

$$\mathrm{Wow}!\mathrm{Thank}\mathrm{you}\mathrm{Sir}.\mathrm{You}\mathrm{understood}\mathrm{me}$$$$\mathrm{perfectly}.$$

Commented by som(math1967) last updated on 29/Jul/20

$$\mathrm{welcome}$$

Answered by Ar Brandon last updated on 28/Jul/20

$$\mathcal{I}=\int \mathrm{tanx}\cdot \tan 2\mathrm{x}\cdot \tan 3\mathrm{x}\cdot \mathrm{dx}$$$$=\int \mathrm{tanx}\cdot \frac{2\mathrm{tanx}}{1-{\tan }^2\mathrm{x}}\cdot \tan 3\mathrm{x}\cdot \mathrm{dx}$$$$=2\int \frac{{\tan }^2\mathrm{x}}{1-{\tan }^2\mathrm{x}}\cdot \tan 3\mathrm{x}\cdot \mathrm{dx}=-2\int \frac{(1-{\tan }^2\mathrm{x})-1}{1-{\tan }^2\mathrm{x}}\cdot \tan 3\mathrm{x}\cdot \mathrm{dx}$$$$=-2\int \{\tan 3\mathrm{x}-\frac{\tan 3\mathrm{x}}{1-{\tan }^2\mathrm{x}}\}\mathrm{dx}=\frac{2\ln \mid \cos 3\mathrm{x}\mid }{3}+2\int \frac{\tan 3\mathrm{x}}{1-{\tan }^2\mathrm{x}}\mathrm{dx}$$$$\tan 3\mathrm{x}=\frac{\tan 2\mathrm{x}+\mathrm{tanx}}{1-\tan 2\mathrm{x}\cdot \mathrm{tanx}}=\frac{\frac{2\mathrm{tanx}}{1-{\tan }^2\mathrm{x}}+\mathrm{tanx}}{1-\frac{2\mathrm{tanx}}{1-{\tan }^2\mathrm{x}}\mathrm{tanx}}$$$$=\frac{2\mathrm{tanx}+\mathrm{tanx}\cdot (1-{\tan }^2\mathrm{x})}{1-{\tan }^2\mathrm{x}-{2\tan }^2\mathrm{x}}=\frac{3\mathrm{tanx}-{\tan }^3\mathrm{x}}{1-{3\tan }^2\mathrm{x}}$$$$=\frac{\mathrm{tanx}({\tan }^2\mathrm{x}-3)}{{3\tan }^2\mathrm{x}-1}=\frac{1}{3}\cdot \frac{\mathrm{tanx}\cdot (({3\tan }^2\mathrm{x}-1)-8)}{{3\tan }^2\mathrm{x}-1}$$$$=\frac{1}{3}\cdot \{\frac{\mathrm{tanx}({3\tan }^2\mathrm{x}-1)}{{3\tan }^2\mathrm{x}-1}-\frac{8\mathrm{tanx}}{{3\tan }^2\mathrm{x}-1}\}$$$$=\frac{1}{3}\cdot \{\mathrm{tanx}-\frac{8\mathrm{tanx}}{{3\tan }^2\mathrm{x}-1}\}$$$$\Rightarrow \frac{\tan 3\mathrm{x}}{1-{\tan }^2\mathrm{x}}=\frac{1}{3}\{\frac{\mathrm{tanx}}{1-{\tan }^2\mathrm{x}}+\frac{8\mathrm{tanx}}{({3\tan }^2\mathrm{x}-1)({\tan }^2\mathrm{x}-1)}\}$$$$$$$$\mathrm{Here}\mathrm{is}\mathrm{my}\mathrm{try}.\mathrm{What}\mathrm{can}\mathrm{be}\mathrm{done}\mathrm{next}?$$

Commented by malwaan last updated on 29/Jul/20

$$trytousetheshortwaysir$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com