Question Number 105474 by Don08q last updated on 29/Jul/20
Answered by ajfour last updated on 29/Jul/20
Commented by ajfour last updated on 29/Jul/20
$${BD}=\sqrt{\mathrm{25}+\mathrm{36}−\mathrm{2}×\mathrm{5}×\mathrm{6cos}\:\mathrm{30}°} \\ $$$$\:\:\:\:\:\:\:\:=\:\sqrt{\mathrm{61}−\mathrm{30}\sqrt{\mathrm{3}}} \\ $$$$\:\:\:\:{BD}=\mathrm{2}{R}\mathrm{sin}\:\mathrm{30}°\:=\:{R} \\ $$$$....... \\ $$
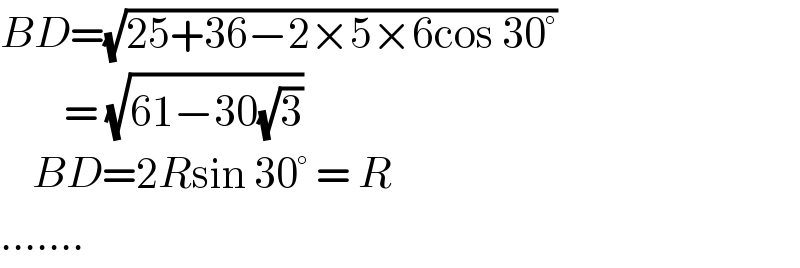
Answered by 1549442205PVT last updated on 29/Jul/20
Commented by 1549442205PVT last updated on 01/Aug/20
![Apply the cosine theorem for ΔABG we get:BG=(√(6^2 +5^2 −2.6.5cos30°))= (√(61−30(√3)))=R(as ΔOBG is isosceles at O and BOG^( ) =2BAG^( ) =60°). we have also AC=(r/(sin15°)),sin15°=(((√6)−(√2))/4),cos15°=(((√6)+(√2))/4) Denote by I the midpoint of side AG we have AI=3⇒OI=(√(R^2 −9)) .Set OAI^( ) =ϕ⇒cosϕ=(3/R),sinϕ=(((√(R^2 −9)) )/R) Apply the cosine theorem for ΔAOC: OC=(√(R^2 +AC^2 −2AC.Rcos(15°+ϕ)))= (√(R^2 +(r^2 /(sin^2 15°))−((2Rr)/(sin15°))×(cos15°cosϕ−sin15°sinϕ))) From the condition that the circle(C)at D tangent to the circle (O)we have OC+CD=R⇔OC=R−r.Hence, (√(R^2 +(r^2 /(sin^2 15°))−((2Rr)/(sin15°))×(cos15°cosϕ−sin15°sinϕ))) R−r.Squaring two sides of above equality we get: R^2 +(r^2 /(sin^2 15°))−((2Rr)/(sin15°))×(cos15°cosϕ−sin15°sinϕ)=R^2 −2Rr+r^2 ⇔((4r^2 )/(2−(√3)))−((8Rr)/((√6)−(√2)))×[((3((√6)+(√2)))/(4R))−((((√6)−(√2))(√(R^2 −9)))/(4R))]=r^2 −2Rr 4(2+(√3))r^2 −(r/2)((√6)+(√2))[3((√6)+(√2)−((√6)−(√2))(√(R^2 −9))] ⇔(7+4(√3))r^2 −3(4+2(√3))r+2r(√(R^2 −9))+2Rr=0 ⇔(7+4(√3))r+[2R−3(4+2(√3))+2(√(52−30(√3) )) )=0 ⇔r=((2(√(61−30(√3))) −3(4+2(√3) )+2(√(52−30(√3))))/(−(7+4(√3) )))≈1,148](Q105502.png)
$$\mathrm{Apply}\:\mathrm{the}\:\mathrm{cosine}\:\mathrm{theorem}\:\mathrm{for}\:\Delta\mathrm{ABG} \\ $$$$\mathrm{we}\:\mathrm{get}:\mathrm{BG}=\sqrt{\mathrm{6}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} −\mathrm{2}.\mathrm{6}.\mathrm{5cos30}°}= \\ $$$$\sqrt{\mathrm{61}−\mathrm{30}\sqrt{\mathrm{3}}}=\mathrm{R}\left(\mathrm{as}\:\Delta\mathrm{OBG}\:\mathrm{is}\:\mathrm{isosceles}\right. \\ $$$$\left.\mathrm{at}\:\mathrm{O}\:\mathrm{and}\:\widehat {\mathrm{BOG}}=\mathrm{2}\widehat {\mathrm{BAG}}=\mathrm{60}°\right). \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{also}\:\mathrm{AC}=\frac{\mathrm{r}}{\mathrm{sin15}°},\mathrm{sin15}°=\frac{\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}}{\mathrm{4}},\mathrm{cos15}°=\frac{\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}}{\mathrm{4}} \\ $$$$\mathrm{Denote}\:\mathrm{by}\:\mathrm{I}\:\mathrm{the}\:\mathrm{midpoint}\:\mathrm{of}\:\mathrm{side}\:\mathrm{AG} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{AI}=\mathrm{3}\Rightarrow\mathrm{OI}=\sqrt{\mathrm{R}^{\mathrm{2}} −\mathrm{9}}\:.\mathrm{Set}\: \\ $$$$\widehat {\mathrm{OAI}}=\varphi\Rightarrow\mathrm{cos}\varphi=\frac{\mathrm{3}}{\mathrm{R}},\mathrm{sin}\varphi=\frac{\sqrt{\mathrm{R}^{\mathrm{2}} −\mathrm{9}}\:}{\mathrm{R}} \\ $$$$\mathrm{Apply}\:\mathrm{the}\:\mathrm{cosine}\:\mathrm{theorem}\:\mathrm{for}\:\Delta\mathrm{AOC}: \\ $$$$\mathrm{OC}=\sqrt{\mathrm{R}^{\mathrm{2}} +\mathrm{AC}^{\mathrm{2}} −\mathrm{2AC}.\mathrm{Rcos}\left(\mathrm{15}°+\varphi\right)}= \\ $$$$\sqrt{\mathrm{R}^{\mathrm{2}} +\frac{\mathrm{r}^{\mathrm{2}} }{\mathrm{sin}^{\mathrm{2}} \mathrm{15}°}−\frac{\mathrm{2Rr}}{\mathrm{sin15}°}×\left(\mathrm{cos15}°\mathrm{cos}\varphi−\mathrm{sin15}°\mathrm{sin}\varphi\right)}\: \\ $$$$\mathrm{From}\:\mathrm{the}\:\mathrm{condition}\:\mathrm{that}\:\mathrm{the}\:\mathrm{circle}\left(\mathrm{C}\right)\mathrm{at}\:\mathrm{D} \\ $$$$\mathrm{tangent}\:\mathrm{to}\:\mathrm{the}\:\mathrm{circle}\:\left(\mathrm{O}\right)\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{OC}+\mathrm{CD}=\mathrm{R}\Leftrightarrow\mathrm{OC}=\mathrm{R}−\mathrm{r}.\mathrm{Hence}, \\ $$$$\sqrt{\mathrm{R}^{\mathrm{2}} +\frac{\mathrm{r}^{\mathrm{2}} }{\mathrm{sin}^{\mathrm{2}} \mathrm{15}°}−\frac{\mathrm{2Rr}}{\mathrm{sin15}°}×\left(\mathrm{cos15}°\mathrm{cos}\varphi−\mathrm{sin15}°\mathrm{sin}\varphi\right)} \\ $$$$\mathrm{R}−\mathrm{r}.\mathrm{Squaring}\:\mathrm{two}\:\mathrm{sides}\:\mathrm{of}\:\mathrm{above}\:\mathrm{equality}\:\mathrm{we}\:\mathrm{get}: \\ $$$$\mathrm{R}^{\mathrm{2}} +\frac{\mathrm{r}^{\mathrm{2}} }{\mathrm{sin}^{\mathrm{2}} \mathrm{15}°}−\frac{\mathrm{2Rr}}{\mathrm{sin15}°}×\left(\mathrm{cos15}°\mathrm{cos}\varphi−\mathrm{sin15}°\mathrm{sin}\varphi\right)=\mathrm{R}^{\mathrm{2}} −\mathrm{2Rr}+\mathrm{r}^{\mathrm{2}} \\ $$$$\Leftrightarrow\frac{\mathrm{4r}^{\mathrm{2}} }{\mathrm{2}−\sqrt{\mathrm{3}}}−\frac{\mathrm{8Rr}}{\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}}×\left[\frac{\mathrm{3}\left(\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}\right)}{\mathrm{4R}}−\frac{\left(\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}\right)\sqrt{\mathrm{R}^{\mathrm{2}} −\mathrm{9}}}{\mathrm{4R}}\right]=\mathrm{r}^{\mathrm{2}} −\mathrm{2Rr} \\ $$$$\mathrm{4}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)\mathrm{r}^{\mathrm{2}} −\frac{\mathrm{r}}{\mathrm{2}}\left(\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}\right)\left[\mathrm{3}\left(\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}−\left(\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}\right)\sqrt{\mathrm{R}^{\mathrm{2}} −\mathrm{9}}\right]\right. \\ $$$$\Leftrightarrow\left(\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}}\right)\mathrm{r}^{\mathrm{2}} −\mathrm{3}\left(\mathrm{4}+\mathrm{2}\sqrt{\mathrm{3}}\right)\mathrm{r}+\mathrm{2r}\sqrt{\mathrm{R}^{\mathrm{2}} −\mathrm{9}}+\mathrm{2Rr}=\mathrm{0} \\ $$$$\Leftrightarrow\left(\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}}\right)\mathrm{r}+\left[\mathrm{2R}−\mathrm{3}\left(\mathrm{4}+\mathrm{2}\sqrt{\mathrm{3}}\right)+\mathrm{2}\sqrt{\mathrm{52}−\mathrm{30}\sqrt{\mathrm{3}}\:}\:\right)=\mathrm{0} \\ $$$$\Leftrightarrow\boldsymbol{\mathrm{r}}=\frac{\mathrm{2}\sqrt{\mathrm{61}−\mathrm{30}\sqrt{\mathrm{3}}}\:−\mathrm{3}\left(\mathrm{4}+\mathrm{2}\sqrt{\mathrm{3}}\:\right)+\mathrm{2}\sqrt{\mathrm{52}−\mathrm{30}\sqrt{\mathrm{3}}}}{−\left(\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}}\:\right)}\approx\mathrm{1},\mathrm{148} \\ $$
Commented by Don08q last updated on 29/Jul/20
$${Thank}\:{you}\:{Sir} \\ $$