calculate ∫_0 ^∞ ((sin x)/x)dx


Question and Answers Forum

All Questions Topic List
Limits Questions
Previous in All Question Next in All Question
Previous in Limits Next in Limits
Question Number 105545 by 4635 last updated on 29/Jul/20

$c a l c u l a t e \int_{0}^{\infty} \frac{\sin x}{x} d x$
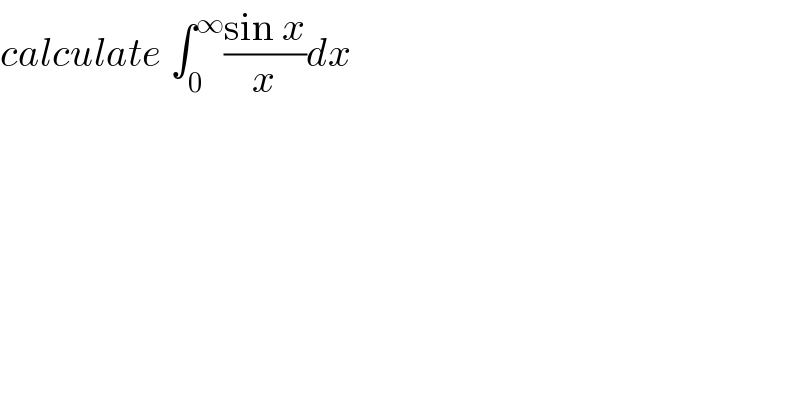
	Answered by Ar Brandon last updated on 29/Jul/20
	$Let f(a)=∫_0 ^∞ ((sinx)/x)∙e^(−ax) dx⇒f ′(a)=−∫_0 ^∞ sinx∙e^(−ax) dx Let; p=∫_0 ^∞ cosx∙e^(−ax) dx , q=∫_0 ^∞ sinx∙e^(−ax) dx ⇒p−iq=∫_0 ^∞ (cosx−isinx)e^(−ax) dx=∫_0 ^∞ e^(−ix−ax) dx=∫_0 ^∞ e^(−(a+i)x) dx =−(1/(a+i))∙[e^(−(a+i)x) ]_0 ^∞ =(1/(a+i)) {lim_(x→∞) e^(−(a+i)x) =0} =((a−i)/(a^2 +1))=(a/(a^2 +1))−i((1/(a^2 +1))) ⇒ Im(p−iq)=Im{(a/(a^2 +1))−i((1/(a^2 +1)))}⇒q=(1/(a^2 +1)) ⇒f ′(a)=−q=−(1/(a^2 +1))⇒f(a)=−[Arctan(a)+C] But f(a)=∫_0 ^∞ ((sinx)/x)∙e^(−ax) dx , lim_(a→+∞) f(a)=0 ⇒lim_(a→+∞) [Arctan(a)+C]=0⇒C=−(π/2) f(0)=∫_0 ^∞ ((sinx)/x)dx=−[Arctan(0)+C]=(π/2) Hence ∫_0 ^∞ ((sinx)/x)dx=(π/2)$
	$Let f (a) = \int_{0}^{\infty} \frac{sinx}{x} \cdot e^{- ax} dx \Rightarrow f^{'} (a) = - \int_{0}^{\infty} sinx \cdot e^{- ax} dx$ $Let; p = \int_{0}^{\infty} cosx \cdot e^{- ax} dx, q = \int_{0}^{\infty} sinx \cdot e^{- ax} dx$ $\Rightarrow p - iq = \int_{0}^{\infty} (cosx - isinx) e^{- ax} dx = \int_{0}^{\infty} e^{- ix - ax} dx = \int_{0}^{\infty} e^{- (a + i) x} dx$ $= - \frac{1}{a + i} \cdot {[e^{- (a + i) x}]}_{0}^{\infty} = \frac{1}{a + i} {{\underset{x \to \infty}{\lim e}}^{- (a + i) x} = 0}$ $= \frac{a - i}{a^{2} + 1} = \frac{a}{a^{2} + 1} - i (\frac{1}{a^{2} + 1})$ $\Rightarrow I m (p - iq) = I m {\frac{a}{a^{2} + 1} - i (\frac{1}{a^{2} + 1})} \Rightarrow q = \frac{1}{a^{2} + 1}$ $\Rightarrow f^{'} (a) = - q = - \frac{1}{a^{2} + 1} \Rightarrow f (a) = - [Arctan (a) + C]$ $But f (a) = \int_{0}^{\infty} \frac{sinx}{x} \cdot e^{- ax} dx, \underset{a \to + \infty}{\lim f} (a) = 0$ $\Rightarrow \lim_{a \to + \infty} [Arctan (a) + C] = 0 \Rightarrow C = - \frac{π}{2}$ $f (0) = \int_{0}^{\infty} \frac{sinx}{x} dx = - [Arctan (0) + C] = \frac{π}{2}$ $Hence \int_{0}^{\infty} \frac{sinx}{x} dx = \frac{π}{2}$
	Answered by Aziztisffola last updated on 29/Jul/20
	$Using Laplace transforms. L{((sinx)/x)}=∫_s ^( ∞) L{sinx}dt=∫_s ^( ∞) (1/(1+t^2 ))dt =[arctan(t)]_s ^(t→∞) =(π/2)−arctan(s) then ∫_0 ^( ∞) e^(−sx) ((sin x)/x) dx=(π/2)−arctan(s) let s=0 ⇒∫_0 ^∞ ((sin x)/x)dx=(π/2)−arctan(0)=(π/2) Hence ∫_0 ^∞ ((sin x)/x)dx=(π/2)$
	$Using Laplace transforms .$ $L {\frac{\sin x}{x}} = \int_{s}^{\infty} L {\sin x} dt = \int_{s}^{\infty} \frac{1}{1 + t^{2}} dt$ $= {[\arctan (t)]}_{s}^{t \to \infty} = \frac{π}{2} - \arctan (s)$ $then \int_{0}^{\infty} e^{- s x} \frac{\sin x}{x} d x = \frac{π}{2} - \arctan (s)$ $let s = 0 \Rightarrow \int_{0}^{\infty} \frac{\sin x}{x} d x = \frac{π}{2} - \arctan (0) = \frac{π}{2}$ $Hence \int_{0}^{\infty} \frac{\sin x}{x} d x = \frac{π}{2}$
	Commented by 4635 last updated on 29/Jul/20

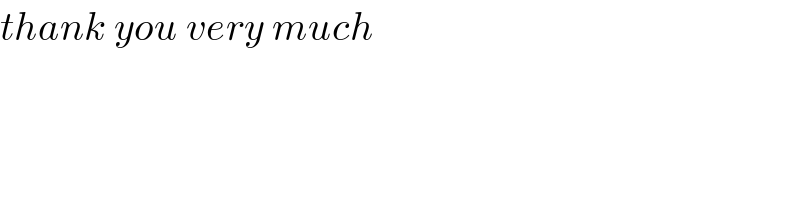
	$t h a n k y o u v e r y m u c h$
	Commented by Aziztisffola last updated on 29/Jul/20

	${you}^{'} re welcome$
	Answered by 1549442205PVT last updated on 30/Jul/20

	$Set I (k, λ) = \int_{0}^{\infty} e^{- kx} \frac{\sin λ x}{x} dx$ $Differentiate the integration I by λ we get$ $\frac{dI}{d λ} = \int_{0}^{\infty} e^{- kx} . \frac{1}{x} . {(\sin λ x)}^{'} dx = \int_{0}^{\infty} e^{- kx} \cos λ xdx$ $= \frac{1}{λ} \int_{0}^{\infty} e^{- kx} dsin λ x = \frac{e^{- kx} \sin λ x}{λ} ∣_{x = 0}^{\infty} + \frac{k}{λ} \int_{0}^{\infty} e^{- kx} \sin λ xdx$ $= \frac{e^{- kx} \sin λ x}{λ} ∣_{0}^{\infty} - \frac{k}{λ^{2}} \int_{0}^{\infty} e^{- kx} dcos λ x$ $= (\frac{e^{- kx} \sin λ x}{λ} - \frac{{ke}^{- kx} \cos λ x}{λ^{2}}) ∣_{0}^{\infty} - \frac{k^{2}}{λ^{2}} \int e^{- kx} \cos λ xdx$ $Thus, \frac{dI}{d λ} = (\frac{e^{- kx} \sin λ x}{λ} - \frac{{ke}^{- kx} \cos λ x}{λ^{2}}) ∣_{0}^{\infty} - \frac{k^{2}}{λ} . \frac{dI}{d λ}$ $\Rightarrow\Rightarrow (1 + \frac{k^{2}}{λ^{2}}) . \frac{dI}{d λ} = (\frac{e^{- kx} \sin λ x}{λ} - \frac{{ke}^{- kx} \cos λ x}{λ^{2}}) ∣_{0}^{\infty}$ $\frac{dI}{d λ} = \frac{e^{- kx} (λ \sin λ x - kcos λ x)}{k^{2} + λ^{2}} ∣_{0}^{\infty} = \frac{k}{λ^{2} + k^{2}}$ $\Rightarrow I = \tan^{- 1} (\frac{λ}{k}) (as \int \frac{dx}{x^{2} + a^{2}} = \frac{1}{a} \tan^{- 1} (\frac{x}{a}))$ $Consequently, I (k, λ) = \int_{0}^{\infty} e^{- kx} \frac{\sin λ x}{x} dx = \tan^{- 1} (\frac{λ}{k})$ $It follows that$ $J = \int_{0}^{\infty} \frac{\sin λ x}{x} dx = \lim_{k \to 0} \int_{0}^{\infty} e^{- kx} \frac{\sin λ x}{x} dx$ $= {\underset{k \to 0}{\lim t a n}}^{- 1} (\frac{λ}{k}) = \frac{π}{2} (if λ > 0)$ $Therefore, K = \int_{0}^{\infty} \frac{sinx}{x} dx = \frac{π}{2}$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum