Solve the differential equation; y′′+4y′+5y=xe^(−2x) sinx


Question and Answers Forum

All Questions Topic List
Differential Equation Questions
Previous in All Question Next in All Question
Previous in Differential Equation Next in Differential Equation
Question Number 105564 by Ar Brandon last updated on 30/Jul/20

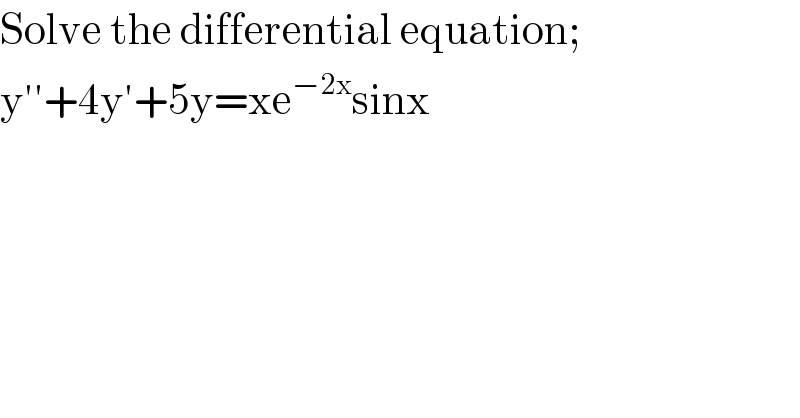
$Solve the differential equation;$ $y^{″} + {4 y}^{'} + 5 y = {xe}^{- 2 x} sinx$
	Answered by bobhans last updated on 30/Jul/20
	$Homogenous equation υ^2 +4υ+5=0 →υ=((−4±2i)/2)=−2±i y_h =e^(−2x) {C_1 cos x+C_2 sin x} particular solution y_1 =e^(−2x) cos x⇒y_1 ′=−2e^(−2x) cos x−e^(−2x) sinx y_2 =e^(−2x) sin x⇒y_2 ′=−2e^(−2x) sin x+e^(−2x) cosx W= determinant ((( e^(−2x) cos x e^(−2x) sin x)),((e^(−2x) (−2cos x−sin x) e^(−2x) (−2sin x+cos x))) = e^(−4x) (−2sin xcos x+cos^2 x)−e^(−4x) (−2sinx cos x −sin^2 x) = e^(−4x) u_1 =−∫ ((e^(−2x) sin x(xe^(−2x) sin x)dx)/e^(−4x) ) u_1 =−∫ xsin^2 x dx = −∫x((1/2)−(1/2)cos2x)dx u_1 =−[(1/4)x^2 −((1/4)xcos 2x−(1/8)sin 2x)] u_1 =−(1/4)x^2 +(1/4)xcos 2x−(1/8)sin 2x u_2 =∫ ((e^(−2x) cos x(xe^(−2x) sin x)dx)/e^(−4x) ) u_2 = ∫(1/2)xsin 2x dx = −(1/4)xcos 2x+(1/(16))sin2x y_p = y_1 u_1 +y_2 u_2 y_p = e^(−2x) cos x(−(1/4)x^2 +(1/4)xcos 2x−(1/8)sin2x) + e^(−2x) sin x(−(1/4)xcos 2x+(1/(16))sin 2x) General solution y_G = y_b + y_p .★$
	$H o m o g e n o u s e q u a t i o n$ $υ^{2} + 4 υ + 5 = 0 \to υ = \frac{- 4 \pm 2 i}{2} = - 2 \pm i$ $y_{h} = e^{- 2 x} {C_{1} \cos x + C_{2} \sin x}$ $p a r t i c u l a r s o l u t i o n$ $y_{1} = e^{- 2 x} \cos x \Rightarrow y_{1}^{'} = - 2 e^{- 2 x} \cos x - e^{- 2 x} \sin x$ $y_{2} = e^{- 2 x} \sin x \Rightarrow y_{2}^{'} = - 2 e^{- 2 x} \sin x + e^{- 2 x} \cos x$ $W = \| \begin{matrix} e^{- 2 x} \cos x e^{- 2 x} \sin x \\ e^{- 2 x} (- 2 \cos x - \sin x) e^{- 2 x} (- 2 \sin x + \cos x \end{matrix} \|$ $= e^{- 4 x} (- 2 \sin x \cos x + \cos^{2} x) - e^{- 4 x} (- 2 \sin x$ $\cos x - \sin^{2} x) = e^{- 4 x}$ $u_{1} = - \int \frac{e^{- 2 x} \sin x ({x e}^{- 2 x} \sin x) d x}{e^{- 4 x}}$ $u_{1} = - \int x \sin^{2} x d x = - \int x (\frac{1}{2} - \frac{1}{2} \cos 2 x) d x$ $u_{1} = - [\frac{1}{4} x^{2} - (\frac{1}{4} x \cos 2 x - \frac{1}{8} \sin 2 x)]$ $u_{1} = - \frac{1}{4} x^{2} + \frac{1}{4} x \cos 2 x - \frac{1}{8} \sin 2 x$ $u_{2} = \int \frac{e^{- 2 x} \cos x ({x e}^{- 2 x} \sin x) d x}{e^{- 4 x}}$ $u_{2} = \int \frac{1}{2} x \sin 2 x d x = - \frac{1}{4} x \cos 2 x + \frac{1}{16} \sin 2 x$ $y_{p} = y_{1} u_{1} + y_{2} u_{2}$ $y_{p} = e^{- 2 x} \cos x (- \frac{1}{4} x^{2} + \frac{1}{4} x \cos 2 x - \frac{1}{8} \sin 2 x)$ $+ e^{- 2 x} \sin x (- \frac{1}{4} x \cos 2 x + \frac{1}{16} \sin 2 x)$ $G e n e r a l s o l u t i o n$ $y_{G} = y_{b} + y_{p} . ★$
	Commented by Ar Brandon last updated on 30/Jul/20
	Thanks, Sir Bobhans. Is this Wronskien's method ?��
	Commented by bobhans last updated on 30/Jul/20

	$y e s s i r .$
	Commented by Ar Brandon last updated on 30/Jul/20
	OK, gracias
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum