Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 105638 by bemath last updated on 30/Jul/20

(d^2 y/dx^2 ) + 9y = cos 4x

$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:+\:\mathrm{9}{y}\:=\:\mathrm{cos}\:\mathrm{4}{x} \\ $$

Answered by bramlex last updated on 30/Jul/20

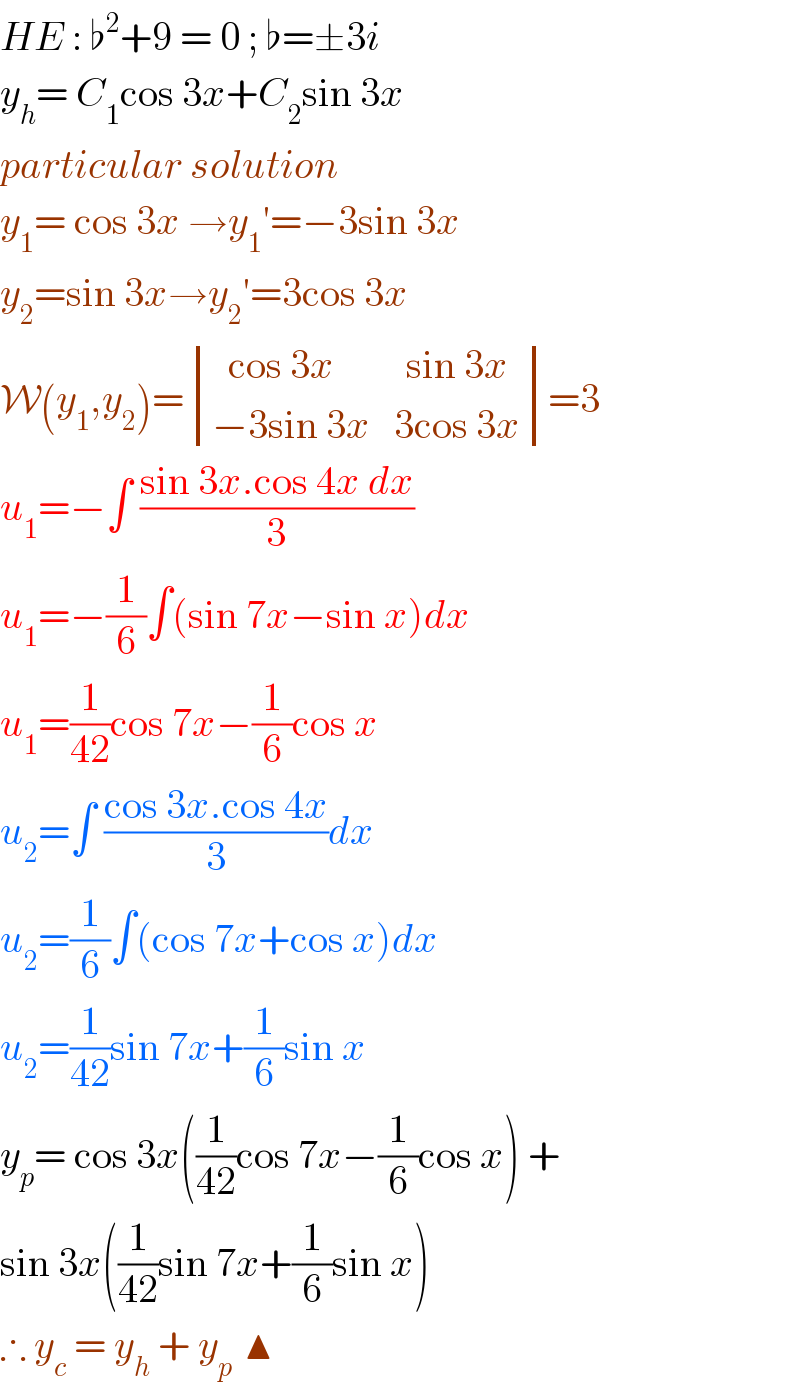
HE : ♭^2 +9 = 0 ; ♭=±3i y_h = C_1 cos 3x+C_2 sin 3x particular solution y_1 = cos 3x →y_1 ′=−3sin 3x y_2 =sin 3x→y_2 ′=3cos 3x W(y_1 ,y_2 )= determinant ((( cos 3x sin 3x)),((−3sin 3x 3cos 3x)))=3 u_1 =−∫ ((sin 3x.cos 4x dx)/3) u_1 =−(1/6)∫(sin 7x−sin x)dx u_1 =(1/(42))cos 7x−(1/6)cos x u_2 =∫ ((cos 3x.cos 4x)/3)dx u_2 =(1/6)∫(cos 7x+cos x)dx u_2 =(1/(42))sin 7x+(1/6)sin x y_p = cos 3x((1/(42))cos 7x−(1/6)cos x) + sin 3x((1/(42))sin 7x+(1/6)sin x) ∴ y_c = y_h + y_(p ) ▲

$${HE}\::\:\flat^{\mathrm{2}} +\mathrm{9}\:=\:\mathrm{0}\:;\:\flat=\pm\mathrm{3}{i} \\ $$$${y}_{{h}} =\:{C}_{\mathrm{1}} \mathrm{cos}\:\mathrm{3}{x}+{C}_{\mathrm{2}} \mathrm{sin}\:\mathrm{3}{x}\: \\ $$$${particular}\:{solution} \\ $$$${y}_{\mathrm{1}} =\:\mathrm{cos}\:\mathrm{3}{x}\:\rightarrow{y}_{\mathrm{1}} '=−\mathrm{3sin}\:\mathrm{3}{x} \\ $$$${y}_{\mathrm{2}} =\mathrm{sin}\:\mathrm{3}{x}\rightarrow{y}_{\mathrm{2}} '=\mathrm{3cos}\:\mathrm{3}{x} \\ $$$$\mathcal{W}\left({y}_{\mathrm{1}} ,{y}_{\mathrm{2}} \right)=\begin{vmatrix}{\:\:\mathrm{cos}\:\mathrm{3}{x}\:\:\:\:\:\:\:\:\:\mathrm{sin}\:\mathrm{3}{x}}\\{−\mathrm{3sin}\:\mathrm{3}{x}\:\:\:\mathrm{3cos}\:\mathrm{3}{x}}\end{vmatrix}=\mathrm{3} \\ $$$${u}_{\mathrm{1}} =−\int\:\frac{\mathrm{sin}\:\mathrm{3}{x}.\mathrm{cos}\:\mathrm{4}{x}\:{dx}}{\mathrm{3}} \\ $$$${u}_{\mathrm{1}} =−\frac{\mathrm{1}}{\mathrm{6}}\int\left(\mathrm{sin}\:\mathrm{7}{x}−\mathrm{sin}\:{x}\right){dx} \\ $$$${u}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{42}}\mathrm{cos}\:\mathrm{7}{x}−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{cos}\:{x} \\ $$$${u}_{\mathrm{2}} =\int\:\frac{\mathrm{cos}\:\mathrm{3}{x}.\mathrm{cos}\:\mathrm{4}{x}}{\mathrm{3}}{dx} \\ $$$${u}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{6}}\int\left(\mathrm{cos}\:\mathrm{7}{x}+\mathrm{cos}\:{x}\right){dx} \\ $$$${u}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{42}}\mathrm{sin}\:\mathrm{7}{x}+\frac{\mathrm{1}}{\mathrm{6}}\mathrm{sin}\:{x} \\ $$$${y}_{{p}} =\:\mathrm{cos}\:\mathrm{3}{x}\left(\frac{\mathrm{1}}{\mathrm{42}}\mathrm{cos}\:\mathrm{7}{x}−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{cos}\:{x}\right)\:+\: \\ $$$$\mathrm{sin}\:\mathrm{3}{x}\left(\frac{\mathrm{1}}{\mathrm{42}}\mathrm{sin}\:\mathrm{7}{x}+\frac{\mathrm{1}}{\mathrm{6}}\mathrm{sin}\:{x}\right) \\ $$$$\therefore\:{y}_{{c}} \:=\:{y}_{{h}} \:+\:{y}_{{p}\:} \:\blacktriangle \\ $$

Answered by mathmax by abdo last updated on 30/Jul/20

y^(′′) +9y =cos(4x) h→r^2 +9 =0 ⇒r =+^− 3i ⇒y_h =a e^(3ix) +b e^(−3ix) =αcos(3x) +βsin(3x) =αu_1 +β u_2 W(u_1 ,u_2 ) = determinant (((cos(3x) sin(3x))),((−3sin(3x) 3cos(3x))))=3cos^2 (3x)+3sin^2 (3x)=3≠0 W_1 = determinant (((o sin(3x))),((cos(4x) 3cos(3x))))=−cos(4x)sin(3x) W_2 = determinant (((cos(3x) 0)),((−3sin(3x) cos(4x))))=cos(3x) cos(4x) v_1 =∫ (w_1 /w)dx =−(1/3) ∫ cos(4x)sin(3x)dx but cos(4x)sin(3x) =cos(4x)cos((π/2)−3x) =(1/2){ cos(x+(π/2))+cos(7x−(π/2))} =(1/2){sin(7x)−sin(x)} ⇒ v_1 =−(1/6)∫ sin(7x)dx +(1/6)∫ sinx dx =(1/(42))cos(7x)−(1/6)cosx v_2 =∫ (w_2 /w)dx =(1/3)∫ cos(3x)cos(4x)dx =(1/6) ∫{cos(7x)+cos(x)}dx =(1/(42))sin(7x)+(1/6)sinx ⇒y_p =u_1 v_(1 ) +u_2 v_2 =cos(3x){(1/(42))cos(7x)−(1/6)cosx} sin(3x){(1/(42))sin(7x)+(1/6)sinx } =(1/(42)){cos(x)cos(7x)+sin(3x)sin(7x)} −(1/6){cosxcos(3x)−sinx sin(3x)} =(1/(42))cos(6x)−(1/6)cos(4x) the general solution is y =y_p +y_h =(1/(42))cos(6x)−(1/6)cos(4x) +αcos(3x) +β sin(3x)

$$\mathrm{y}^{''} \:+\mathrm{9y}\:=\mathrm{cos}\left(\mathrm{4x}\right) \\ $$$$\mathrm{h}\rightarrow\mathrm{r}^{\mathrm{2}} \:+\mathrm{9}\:=\mathrm{0}\:\:\Rightarrow\mathrm{r}\:=\overset{−} {+}\mathrm{3i}\:\Rightarrow\mathrm{y}_{\mathrm{h}} =\mathrm{a}\:\mathrm{e}^{\mathrm{3ix}} \:+\mathrm{b}\:\mathrm{e}^{−\mathrm{3ix}} \:=\alpha\mathrm{cos}\left(\mathrm{3x}\right)\:+\beta\mathrm{sin}\left(\mathrm{3x}\right) \\ $$$$=\alpha\mathrm{u}_{\mathrm{1}} \:+\beta\:\mathrm{u}_{\mathrm{2}} \\ $$$$\mathrm{W}\left(\mathrm{u}_{\mathrm{1}} \:,\mathrm{u}_{\mathrm{2}} \right)\:=\begin{vmatrix}{\mathrm{cos}\left(\mathrm{3x}\right)\:\:\:\:\:\:\:\:\:\mathrm{sin}\left(\mathrm{3x}\right)}\\{−\mathrm{3sin}\left(\mathrm{3x}\right)\:\:\:\:\:\:\:\mathrm{3cos}\left(\mathrm{3x}\right)}\end{vmatrix}=\mathrm{3cos}^{\mathrm{2}} \left(\mathrm{3x}\right)+\mathrm{3sin}^{\mathrm{2}} \left(\mathrm{3x}\right)=\mathrm{3}\neq\mathrm{0} \\ $$$$\mathrm{W}_{\mathrm{1}} =\begin{vmatrix}{\mathrm{o}\:\:\:\:\:\:\:\:\:\:\mathrm{sin}\left(\mathrm{3x}\right)}\\{\mathrm{cos}\left(\mathrm{4x}\right)\:\:\mathrm{3cos}\left(\mathrm{3x}\right)}\end{vmatrix}=−\mathrm{cos}\left(\mathrm{4x}\right)\mathrm{sin}\left(\mathrm{3x}\right) \\ $$$$\mathrm{W}_{\mathrm{2}} =\begin{vmatrix}{\mathrm{cos}\left(\mathrm{3x}\right)\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{−\mathrm{3sin}\left(\mathrm{3x}\right)\:\:\:\:\:\mathrm{cos}\left(\mathrm{4x}\right)}\end{vmatrix}=\mathrm{cos}\left(\mathrm{3x}\right)\:\mathrm{cos}\left(\mathrm{4x}\right) \\ $$$$\mathrm{v}_{\mathrm{1}} =\int\:\frac{\mathrm{w}_{\mathrm{1}} }{\mathrm{w}}\mathrm{dx}\:=−\frac{\mathrm{1}}{\mathrm{3}}\:\int\:\mathrm{cos}\left(\mathrm{4x}\right)\mathrm{sin}\left(\mathrm{3x}\right)\mathrm{dx}\:\:\mathrm{but} \\ $$$$\mathrm{cos}\left(\mathrm{4x}\right)\mathrm{sin}\left(\mathrm{3x}\right)\:=\mathrm{cos}\left(\mathrm{4x}\right)\mathrm{cos}\left(\frac{\pi}{\mathrm{2}}−\mathrm{3x}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\mathrm{cos}\left(\mathrm{x}+\frac{\pi}{\mathrm{2}}\right)+\mathrm{cos}\left(\mathrm{7x}−\frac{\pi}{\mathrm{2}}\right)\right\}\:=\frac{\mathrm{1}}{\mathrm{2}}\left\{\mathrm{sin}\left(\mathrm{7x}\right)−\mathrm{sin}\left(\mathrm{x}\right)\right\}\:\Rightarrow \\ $$$$\mathrm{v}_{\mathrm{1}} =−\frac{\mathrm{1}}{\mathrm{6}}\int\:\mathrm{sin}\left(\mathrm{7x}\right)\mathrm{dx}\:+\frac{\mathrm{1}}{\mathrm{6}}\int\:\mathrm{sinx}\:\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{42}}\mathrm{cos}\left(\mathrm{7x}\right)−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{cosx} \\ $$$$\mathrm{v}_{\mathrm{2}} =\int\:\frac{\mathrm{w}_{\mathrm{2}} }{\mathrm{w}}\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{3}}\int\:\mathrm{cos}\left(\mathrm{3x}\right)\mathrm{cos}\left(\mathrm{4x}\right)\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\:\int\left\{\mathrm{cos}\left(\mathrm{7x}\right)+\mathrm{cos}\left(\mathrm{x}\right)\right\}\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{42}}\mathrm{sin}\left(\mathrm{7x}\right)+\frac{\mathrm{1}}{\mathrm{6}}\mathrm{sinx} \\ $$$$\Rightarrow\mathrm{y}_{\mathrm{p}} =\mathrm{u}_{\mathrm{1}} \mathrm{v}_{\mathrm{1}\:} \:+\mathrm{u}_{\mathrm{2}} \mathrm{v}_{\mathrm{2}} =\mathrm{cos}\left(\mathrm{3x}\right)\left\{\frac{\mathrm{1}}{\mathrm{42}}\mathrm{cos}\left(\mathrm{7x}\right)−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{cosx}\right\} \\ $$$$\mathrm{sin}\left(\mathrm{3x}\right)\left\{\frac{\mathrm{1}}{\mathrm{42}}\mathrm{sin}\left(\mathrm{7x}\right)+\frac{\mathrm{1}}{\mathrm{6}}\mathrm{sinx}\:\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{42}}\left\{\mathrm{cos}\left(\mathrm{x}\right)\mathrm{cos}\left(\mathrm{7x}\right)+\mathrm{sin}\left(\mathrm{3x}\right)\mathrm{sin}\left(\mathrm{7x}\right)\right\}\:−\frac{\mathrm{1}}{\mathrm{6}}\left\{\mathrm{cosxcos}\left(\mathrm{3x}\right)−\mathrm{sinx}\:\mathrm{sin}\left(\mathrm{3x}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{42}}\mathrm{cos}\left(\mathrm{6x}\right)−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{cos}\left(\mathrm{4x}\right)\:\mathrm{the}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{is} \\ $$$$\mathrm{y}\:=\mathrm{y}_{\mathrm{p}} \:+\mathrm{y}_{\mathrm{h}} =\frac{\mathrm{1}}{\mathrm{42}}\mathrm{cos}\left(\mathrm{6x}\right)−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{cos}\left(\mathrm{4x}\right)\:+\alpha\mathrm{cos}\left(\mathrm{3x}\right)\:+\beta\:\mathrm{sin}\left(\mathrm{3x}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com