Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 10564 by FilupS last updated on 18/Feb/17

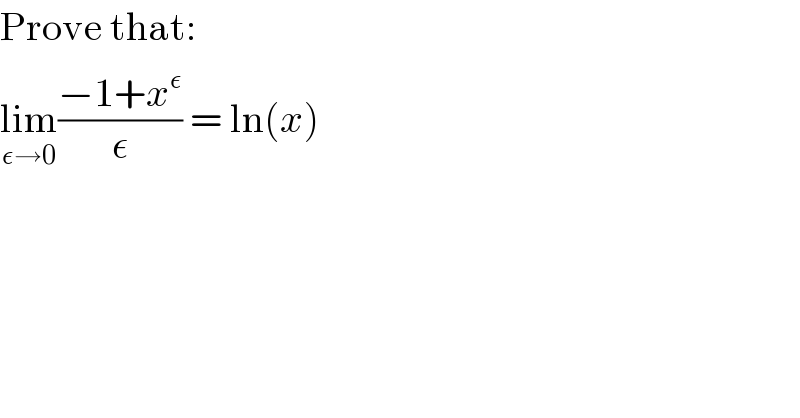
Prove that: lim_(ε→0) ((−1+x^ε )/ε) = ln(x)

$$\mathrm{Prove}\:\mathrm{that}: \\ $$$$\underset{\epsilon\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{1}+{x}^{\epsilon} }{\epsilon}\:=\:\mathrm{ln}\left({x}\right) \\ $$

Answered by lee last updated on 21/Feb/17

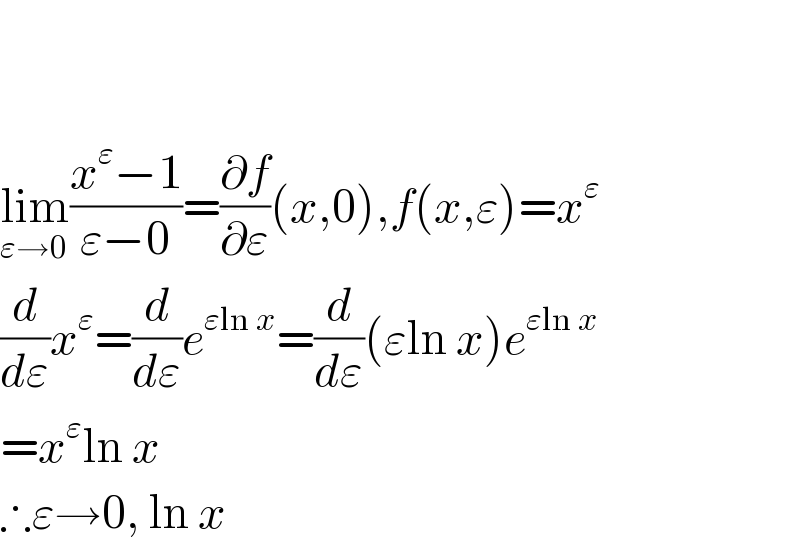
lim_(ε→0) ((x^ε −1)/(ε−0))=(∂f/∂ε)(x,0),f(x,ε)=x^ε (d/dε)x^ε =(d/dε)e^(εln x) =(d/dε)(εln x)e^(εln x) =x^ε ln x ∴ε→0, ln x

$$ \\ $$$$ \\ $$$$\underset{\varepsilon\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}^{\varepsilon} −\mathrm{1}}{\varepsilon−\mathrm{0}}=\frac{\partial{f}}{\partial\varepsilon}\left({x},\mathrm{0}\right),{f}\left({x},\varepsilon\right)={x}^{\varepsilon} \\ $$$$\frac{{d}}{{d}\varepsilon}{x}^{\varepsilon} =\frac{{d}}{{d}\varepsilon}{e}^{\varepsilon\mathrm{ln}\:{x}} =\frac{{d}}{{d}\varepsilon}\left(\varepsilon\mathrm{ln}\:{x}\right){e}^{\varepsilon\mathrm{ln}\:{x}} \\ $$$$={x}^{\varepsilon} \mathrm{ln}\:{x} \\ $$$$\therefore\varepsilon\rightarrow\mathrm{0},\:\mathrm{ln}\:{x} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com