Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 105687 by bramlex last updated on 31/Jul/20

{ ((x^2 +y^2 = 13)),((x^3 +y^3 = 35 )) :}

$$\begin{cases}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \:=\:\mathrm{13}}\\{{x}^{\mathrm{3}} +{y}^{\mathrm{3}} \:=\:\mathrm{35}\:}\end{cases} \\ $$

Answered by john santu last updated on 31/Jul/20

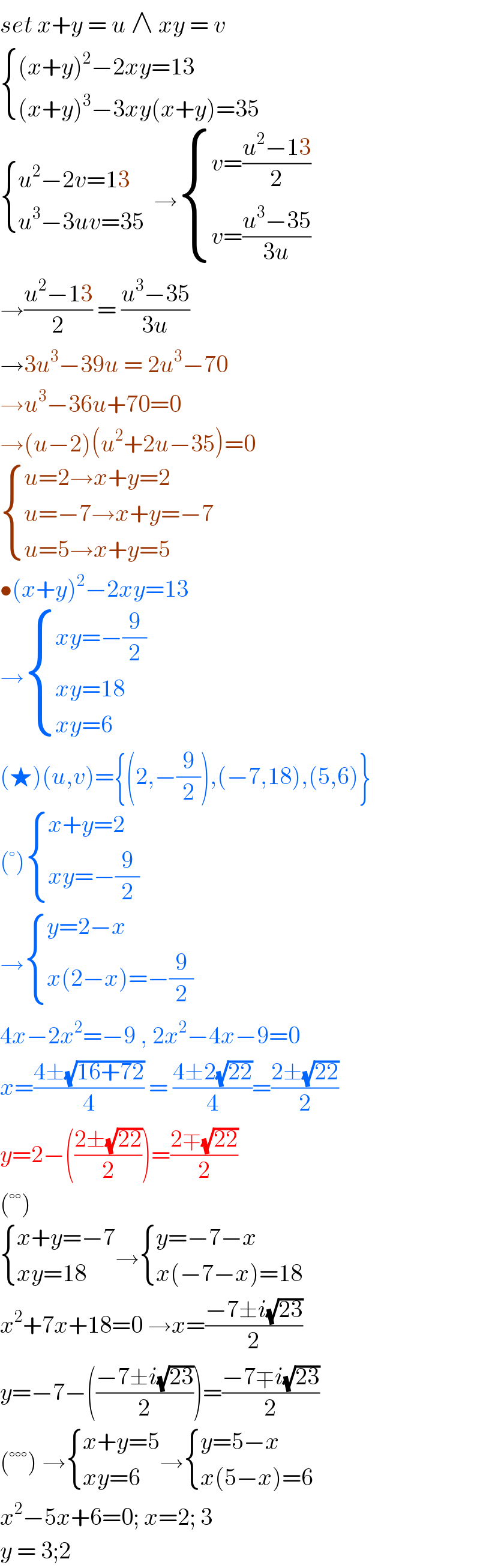
set x+y = u ∧ xy = v { (((x+y)^2 −2xy=13)),(((x+y)^3 −3xy(x+y)=35)) :} { ((u^2 −2v=13)),((u^3 −3uv=35 )) :} → { ((v=((u^2 −13)/2))),((v=((u^3 −35)/(3u)))) :} →((u^2 −13)/2) = ((u^3 −35)/(3u)) →3u^3 −39u = 2u^3 −70 →u^3 −36u+70=0 →(u−2)(u^2 +2u−35)=0 { ((u=2→x+y=2)),((u=−7→x+y=−7)),((u=5→x+y=5)) :} •(x+y)^2 −2xy=13 → { ((xy=−(9/2))),((xy=18)),((xy=6)) :} (★)(u,v)={(2,−(9/2)),(−7,18),(5,6)} (°) { ((x+y=2)),((xy=−(9/2))) :} → { ((y=2−x)),((x(2−x)=−(9/2))) :} 4x−2x^2 =−9 , 2x^2 −4x−9=0 x=((4±(√(16+72)))/4) = ((4±2(√(22)))/4)=((2±(√(22)))/2) y=2−(((2±(√(22)))/2))=((2∓(√(22)))/2) (°°) { ((x+y=−7)),((xy=18)) :}→ { ((y=−7−x)),((x(−7−x)=18)) :} x^2 +7x+18=0 →x=((−7±i(√(23)))/2) y=−7−(((−7±i(√(23)))/2))=((−7∓i(√(23)))/2) (°°°) → { ((x+y=5)),((xy=6)) :}→ { ((y=5−x)),((x(5−x)=6)) :} x^2 −5x+6=0; x=2; 3 y = 3;2

$${set}\:{x}+{y}\:=\:{u}\:\wedge\:{xy}\:=\:{v}\: \\ $$$$\begin{cases}{\left({x}+{y}\right)^{\mathrm{2}} −\mathrm{2}{xy}=\mathrm{13}}\\{\left({x}+{y}\right)^{\mathrm{3}} −\mathrm{3}{xy}\left({x}+{y}\right)=\mathrm{35}}\end{cases} \\ $$$$\begin{cases}{{u}^{\mathrm{2}} −\mathrm{2}{v}=\mathrm{13}}\\{{u}^{\mathrm{3}} −\mathrm{3}{uv}=\mathrm{35}\:}\end{cases}\:\rightarrow\begin{cases}{{v}=\frac{{u}^{\mathrm{2}} −\mathrm{13}}{\mathrm{2}}}\\{{v}=\frac{{u}^{\mathrm{3}} −\mathrm{35}}{\mathrm{3}{u}}}\end{cases} \\ $$$$\rightarrow\frac{{u}^{\mathrm{2}} −\mathrm{13}}{\mathrm{2}}\:=\:\frac{{u}^{\mathrm{3}} −\mathrm{35}}{\mathrm{3}{u}} \\ $$$$\rightarrow\mathrm{3}{u}^{\mathrm{3}} −\mathrm{39}{u}\:=\:\mathrm{2}{u}^{\mathrm{3}} −\mathrm{70}\: \\ $$$$\rightarrow{u}^{\mathrm{3}} −\mathrm{36}{u}+\mathrm{70}=\mathrm{0}\: \\ $$$$\rightarrow\left({u}−\mathrm{2}\right)\left({u}^{\mathrm{2}} +\mathrm{2}{u}−\mathrm{35}\right)=\mathrm{0} \\ $$$$\begin{cases}{{u}=\mathrm{2}\rightarrow{x}+{y}=\mathrm{2}}\\{{u}=−\mathrm{7}\rightarrow{x}+{y}=−\mathrm{7}}\\{{u}=\mathrm{5}\rightarrow{x}+{y}=\mathrm{5}}\end{cases} \\ $$$$\bullet\left({x}+{y}\right)^{\mathrm{2}} −\mathrm{2}{xy}=\mathrm{13} \\ $$$$\rightarrow\begin{cases}{{xy}=−\frac{\mathrm{9}}{\mathrm{2}}}\\{{xy}=\mathrm{18}}\\{{xy}=\mathrm{6}}\end{cases} \\ $$$$\left(\bigstar\right)\left({u},{v}\right)=\left\{\left(\mathrm{2},−\frac{\mathrm{9}}{\mathrm{2}}\right),\left(−\mathrm{7},\mathrm{18}\right),\left(\mathrm{5},\mathrm{6}\right)\right\} \\ $$$$\left(°\right)\begin{cases}{{x}+{y}=\mathrm{2}}\\{{xy}=−\frac{\mathrm{9}}{\mathrm{2}}}\end{cases} \\ $$$$\rightarrow\begin{cases}{{y}=\mathrm{2}−{x}}\\{{x}\left(\mathrm{2}−{x}\right)=−\frac{\mathrm{9}}{\mathrm{2}}}\end{cases} \\ $$$$\mathrm{4}{x}−\mathrm{2}{x}^{\mathrm{2}} =−\mathrm{9}\:,\:\mathrm{2}{x}^{\mathrm{2}} −\mathrm{4}{x}−\mathrm{9}=\mathrm{0} \\ $$$${x}=\frac{\mathrm{4}\pm\sqrt{\mathrm{16}+\mathrm{72}}}{\mathrm{4}}\:=\:\frac{\mathrm{4}\pm\mathrm{2}\sqrt{\mathrm{22}}}{\mathrm{4}}=\frac{\mathrm{2}\pm\sqrt{\mathrm{22}}}{\mathrm{2}} \\ $$$${y}=\mathrm{2}−\left(\frac{\mathrm{2}\pm\sqrt{\mathrm{22}}}{\mathrm{2}}\right)=\frac{\mathrm{2}\mp\sqrt{\mathrm{22}}}{\mathrm{2}} \\ $$$$\left(°°\right) \\ $$$$\begin{cases}{{x}+{y}=−\mathrm{7}}\\{{xy}=\mathrm{18}}\end{cases}\rightarrow\begin{cases}{{y}=−\mathrm{7}−{x}}\\{{x}\left(−\mathrm{7}−{x}\right)=\mathrm{18}}\end{cases} \\ $$$${x}^{\mathrm{2}} +\mathrm{7}{x}+\mathrm{18}=\mathrm{0}\:\rightarrow{x}=\frac{−\mathrm{7}\pm{i}\sqrt{\mathrm{23}}}{\mathrm{2}} \\ $$$${y}=−\mathrm{7}−\left(\frac{−\mathrm{7}\pm{i}\sqrt{\mathrm{23}}}{\mathrm{2}}\right)=\frac{−\mathrm{7}\mp{i}\sqrt{\mathrm{23}}}{\mathrm{2}} \\ $$$$\left(°°°\right)\:\rightarrow\begin{cases}{{x}+{y}=\mathrm{5}}\\{{xy}=\mathrm{6}}\end{cases}\rightarrow\begin{cases}{{y}=\mathrm{5}−{x}}\\{{x}\left(\mathrm{5}−{x}\right)=\mathrm{6}}\end{cases} \\ $$$${x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{6}=\mathrm{0};\:{x}=\mathrm{2};\:\mathrm{3} \\ $$$${y}\:=\:\mathrm{3};\mathrm{2}\: \\ $$

Commented by bramlex last updated on 31/Jul/20

waw...big thanks

$${waw}...{big}\:{thanks}\: \\ $$

Answered by Rasheed.Sindhi last updated on 31/Jul/20

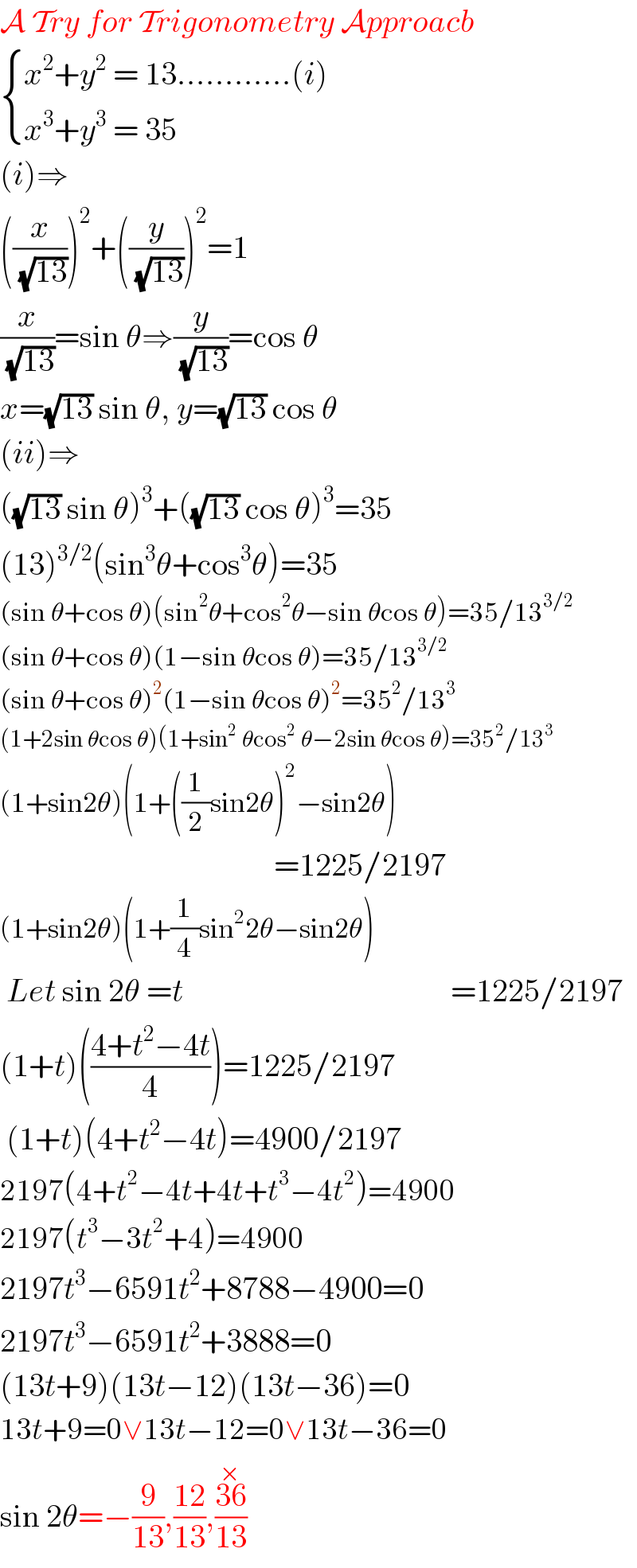
A Try for Trigonometry Approacb { ((x^2 +y^2 = 13............(i))),((x^3 +y^3 = 35 )) :} (i)⇒ ((x/(√(13))))^2 +((y/(√(13))))^2 =1 (x/(√(13)))=sin θ⇒(y/(√(13)))=cos θ x=(√(13)) sin θ, y=(√(13)) cos θ (ii)⇒ ((√(13)) sin θ)^3 +((√(13)) cos θ)^3 =35 (13)^(3/2) (sin^3 θ+cos^3 θ)=35 (sin θ+cos θ)(sin^2 θ+cos^2 θ−sin θcos θ)=35/13^(3/2) (sin θ+cos θ)(1−sin θcos θ)=35/13^(3/2) (sin θ+cos θ)^2 (1−sin θcos θ)^2 =35^2 /13^3 (1+2sin θcos θ)(1+sin^2 θcos^2 θ−2sin θcos θ)=35^2 /13^3 (1+sin2θ)(1+((1/2)sin2θ)^2 −sin2θ) =1225/2197 (1+sin2θ)(1+(1/4)sin^2 2θ−sin2θ) Let sin 2θ =t =1225/2197 (1+t)(((4+t^2 −4t)/4))=1225/2197 (1+t)(4+t^2 −4t)=4900/2197 2197(4+t^2 −4t+4t+t^3 −4t^2 )=4900 2197(t^3 −3t^2 +4)=4900 2197t^3 −6591t^2 +8788−4900=0 2197t^3 −6591t^2 +3888=0 (13t+9)(13t−12)(13t−36)=0 13t+9=0∨13t−12=0∨13t−36=0 sin 2θ=−(9/(13)),((12)/(13)),((36^(×) )/(13))

$$\mathcal{A}\:\mathcal{T}{ry}\:{for}\:\mathcal{T}{rigonometry}\:\mathcal{A}{pproacb} \\ $$$$\begin{cases}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \:=\:\mathrm{13}............\left({i}\right)}\\{{x}^{\mathrm{3}} +{y}^{\mathrm{3}} \:=\:\mathrm{35}\:}\end{cases}\:\:\: \\ $$$$\left({i}\right)\Rightarrow \\ $$$$\left(\frac{{x}}{\sqrt{\mathrm{13}}}\right)^{\mathrm{2}} +\left(\frac{{y}}{\sqrt{\mathrm{13}}}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\frac{{x}}{\sqrt{\mathrm{13}}}=\mathrm{sin}\:\theta\Rightarrow\frac{{y}}{\sqrt{\mathrm{13}}}=\mathrm{cos}\:\theta \\ $$$${x}=\sqrt{\mathrm{13}}\:\mathrm{sin}\:\theta,\:{y}=\sqrt{\mathrm{13}}\:\mathrm{cos}\:\theta \\ $$$$\left({ii}\right)\Rightarrow \\ $$$$\left(\sqrt{\mathrm{13}}\:\mathrm{sin}\:\theta\right)^{\mathrm{3}} +\left(\sqrt{\mathrm{13}}\:\mathrm{cos}\:\theta\right)^{\mathrm{3}} =\mathrm{35} \\ $$$$\left(\mathrm{13}\right)^{\mathrm{3}/\mathrm{2}} \left(\mathrm{sin}^{\mathrm{3}} \theta+\mathrm{cos}^{\mathrm{3}} \theta\right)=\mathrm{35} \\ $$$$\left(\mathrm{sin}\:\theta+\mathrm{cos}\:\theta\right)\left(\mathrm{sin}^{\mathrm{2}} \theta+\mathrm{cos}^{\mathrm{2}} \theta−\mathrm{sin}\:\theta\mathrm{cos}\:\theta\right)=\mathrm{35}/\mathrm{13}^{\mathrm{3}/\mathrm{2}} \\ $$$$\left(\mathrm{sin}\:\theta+\mathrm{cos}\:\theta\right)\left(\mathrm{1}−\mathrm{sin}\:\theta\mathrm{cos}\:\theta\right)=\mathrm{35}/\mathrm{13}^{\mathrm{3}/\mathrm{2}} \\ $$$$\left(\mathrm{sin}\:\theta+\mathrm{cos}\:\theta\right)^{\mathrm{2}} \left(\mathrm{1}−\mathrm{sin}\:\theta\mathrm{cos}\:\theta\right)^{\mathrm{2}} =\mathrm{35}^{\mathrm{2}} /\mathrm{13}^{\mathrm{3}} \\ $$$$\left(\mathrm{1}+\mathrm{2sin}\:\theta\mathrm{cos}\:\theta\right)\left(\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \:\theta\mathrm{cos}^{\mathrm{2}} \:\theta−\mathrm{2sin}\:\theta\mathrm{cos}\:\theta\right)=\mathrm{35}^{\mathrm{2}} /\mathrm{13}^{\mathrm{3}} \\ $$$$\left(\mathrm{1}+\mathrm{sin2}\theta\right)\left(\mathrm{1}+\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin2}\theta\right)^{\mathrm{2}} −\mathrm{sin2}\theta\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{1225}/\mathrm{2197} \\ $$$$\left(\mathrm{1}+\mathrm{sin2}\theta\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}^{\mathrm{2}} \mathrm{2}\theta−\mathrm{sin2}\theta\right) \\ $$$$\:{Let}\:\mathrm{sin}\:\mathrm{2}\theta\:={t}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{1225}/\mathrm{2197} \\ $$$$\left(\mathrm{1}+{t}\right)\left(\frac{\mathrm{4}+{t}^{\mathrm{2}} −\mathrm{4}{t}}{\mathrm{4}}\right)=\mathrm{1225}/\mathrm{2197} \\ $$$$\:\left(\mathrm{1}+{t}\right)\left(\mathrm{4}+{t}^{\mathrm{2}} −\mathrm{4}{t}\right)=\mathrm{4900}/\mathrm{2197} \\ $$$$\mathrm{2197}\left(\mathrm{4}+{t}^{\mathrm{2}} −\mathrm{4}{t}+\mathrm{4}{t}+{t}^{\mathrm{3}} −\mathrm{4}{t}^{\mathrm{2}} \right)=\mathrm{4900} \\ $$$$\mathrm{2197}\left({t}^{\mathrm{3}} −\mathrm{3}{t}^{\mathrm{2}} +\mathrm{4}\right)=\mathrm{4900} \\ $$$$\mathrm{2197}{t}^{\mathrm{3}} −\mathrm{6591}{t}^{\mathrm{2}} +\mathrm{8788}−\mathrm{4900}=\mathrm{0} \\ $$$$\mathrm{2197}{t}^{\mathrm{3}} −\mathrm{6591}{t}^{\mathrm{2}} +\mathrm{3888}=\mathrm{0} \\ $$$$\left(\mathrm{13}{t}+\mathrm{9}\right)\left(\mathrm{13}{t}−\mathrm{12}\right)\left(\mathrm{13}{t}−\mathrm{36}\right)=\mathrm{0} \\ $$$$\mathrm{13}{t}+\mathrm{9}=\mathrm{0}\vee\mathrm{13}{t}−\mathrm{12}=\mathrm{0}\vee\mathrm{13}{t}−\mathrm{36}=\mathrm{0} \\ $$$$\mathrm{sin}\:\mathrm{2}\theta=−\frac{\mathrm{9}}{\mathrm{13}},\frac{\mathrm{12}}{\mathrm{13}},\frac{\overset{×} {\mathrm{36}}}{\mathrm{13}} \\ $$

Answered by Rasheed.Sindhi last updated on 31/Jul/20

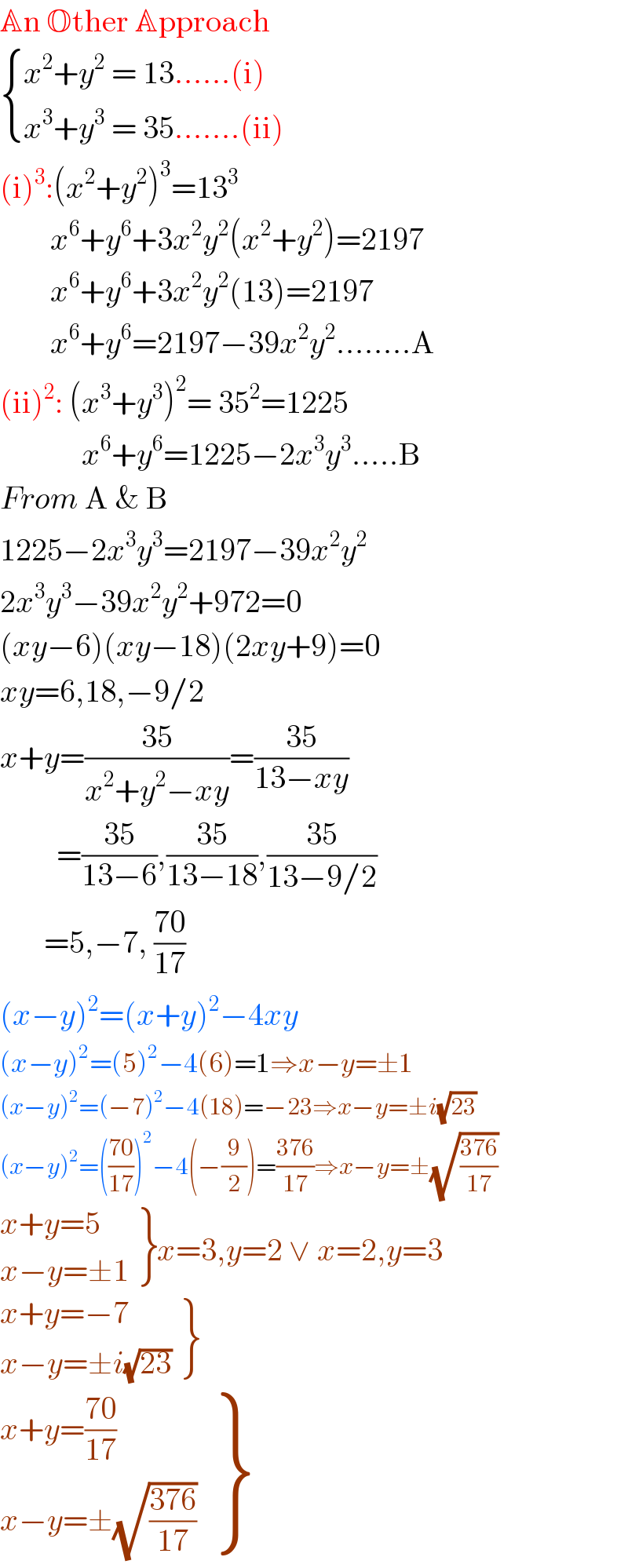
An Other Approach { ((x^2 +y^2 = 13......(i))),((x^3 +y^3 = 35.......(ii) )) :} (i)^3 :(x^2 +y^2 )^3 =13^3 x^6 +y^6 +3x^2 y^2 (x^2 +y^2 )=2197 x^6 +y^6 +3x^2 y^2 (13)=2197 x^6 +y^6 =2197−39x^2 y^2 ........A (ii)^2 : (x^3 +y^3 )^2 = 35^2 =1225 x^6 +y^6 =1225−2x^3 y^3 .....B From A & B 1225−2x^3 y^3 =2197−39x^2 y^2 2x^3 y^3 −39x^2 y^2 +972=0 (xy−6)(xy−18)(2xy+9)=0 xy=6,18,−9/2 x+y=((35)/(x^2 +y^2 −xy))=((35)/(13−xy)) =((35)/(13−6)),((35)/(13−18)),((35)/(13−9/2)) =5,−7, ((70)/(17)) (x−y)^2 =(x+y)^2 −4xy (x−y)^2 =(5)^2 −4(6)=1⇒x−y=±1 (x−y)^2 =(−7)^2 −4(18)=−23⇒x−y=±i(√(23)) (x−y)^2 =(((70)/(17)))^2 −4(−(9/2))=((376)/(17))⇒x−y=±(√((376)/(17))) {: ((x+y=5)),((x−y=±1)) }x=3,y=2 ∨ x=2,y=3 {: ((x+y=−7)),((x−y=±i(√(23)))) } {: ((x+y=((70)/(17)))),((x−y=±(√((376)/(17))))) }

$$\mathbb{A}\mathrm{n}\:\mathbb{O}\mathrm{ther}\:\mathbb{A}\mathrm{pproach} \\ $$$$\begin{cases}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \:=\:\mathrm{13}......\left(\mathrm{i}\right)}\\{{x}^{\mathrm{3}} +{y}^{\mathrm{3}} \:=\:\mathrm{35}.......\left(\mathrm{ii}\right)\:}\end{cases} \\ $$$$\left(\mathrm{i}\right)^{\mathrm{3}} :\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)^{\mathrm{3}} =\mathrm{13}^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:{x}^{\mathrm{6}} +{y}^{\mathrm{6}} +\mathrm{3}{x}^{\mathrm{2}} {y}^{\mathrm{2}} \left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)=\mathrm{2197} \\ $$$$\:\:\:\:\:\:\:\:{x}^{\mathrm{6}} +{y}^{\mathrm{6}} +\mathrm{3}{x}^{\mathrm{2}} {y}^{\mathrm{2}} \left(\mathrm{13}\right)=\mathrm{2197} \\ $$$$\:\:\:\:\:\:\:\:{x}^{\mathrm{6}} +{y}^{\mathrm{6}} =\mathrm{2197}−\mathrm{39}{x}^{\mathrm{2}} {y}^{\mathrm{2}} ........\mathrm{A} \\ $$$$\left(\mathrm{ii}\right)^{\mathrm{2}} :\:\left({x}^{\mathrm{3}} +{y}^{\mathrm{3}} \right)^{\mathrm{2}} =\:\mathrm{35}^{\mathrm{2}} =\mathrm{1225} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{6}} +{y}^{\mathrm{6}} =\mathrm{1225}−\mathrm{2}{x}^{\mathrm{3}} {y}^{\mathrm{3}} .....\mathrm{B} \\ $$$${From}\:\mathrm{A}\:\&\:\mathrm{B} \\ $$$$\mathrm{1225}−\mathrm{2}{x}^{\mathrm{3}} {y}^{\mathrm{3}} =\mathrm{2197}−\mathrm{39}{x}^{\mathrm{2}} {y}^{\mathrm{2}} \\ $$$$\mathrm{2}{x}^{\mathrm{3}} {y}^{\mathrm{3}} −\mathrm{39}{x}^{\mathrm{2}} {y}^{\mathrm{2}} +\mathrm{972}=\mathrm{0} \\ $$$$\left({xy}−\mathrm{6}\right)\left({xy}−\mathrm{18}\right)\left(\mathrm{2}{xy}+\mathrm{9}\right)=\mathrm{0} \\ $$$${xy}=\mathrm{6},\mathrm{18},−\mathrm{9}/\mathrm{2} \\ $$$${x}+{y}=\frac{\mathrm{35}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −{xy}}=\frac{\mathrm{35}}{\mathrm{13}−{xy}} \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\mathrm{35}}{\mathrm{13}−\mathrm{6}},\frac{\mathrm{35}}{\mathrm{13}−\mathrm{18}},\frac{\mathrm{35}}{\mathrm{13}−\mathrm{9}/\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:=\mathrm{5},−\mathrm{7},\:\frac{\mathrm{70}}{\mathrm{17}} \\ $$$$\left({x}−{y}\right)^{\mathrm{2}} =\left({x}+{y}\right)^{\mathrm{2}} −\mathrm{4}{xy} \\ $$$$\left({x}−{y}\right)^{\mathrm{2}} =\left(\mathrm{5}\right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{6}\right)=\mathrm{1}\Rightarrow{x}−{y}=\pm\mathrm{1} \\ $$$$\left({x}−{y}\right)^{\mathrm{2}} =\left(−\mathrm{7}\right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{18}\right)=−\mathrm{23}\Rightarrow{x}−{y}=\pm{i}\sqrt{\mathrm{23}} \\ $$$$\left({x}−{y}\right)^{\mathrm{2}} =\left(\frac{\mathrm{70}}{\mathrm{17}}\right)^{\mathrm{2}} −\mathrm{4}\left(−\frac{\mathrm{9}}{\mathrm{2}}\right)=\frac{\mathrm{376}}{\mathrm{17}}\Rightarrow{x}−{y}=\pm\sqrt{\frac{\mathrm{376}}{\mathrm{17}}} \\ $$$$\left.\begin{matrix}{{x}+{y}=\mathrm{5}}\\{{x}−{y}=\pm\mathrm{1}}\end{matrix}\right\}{x}=\mathrm{3},{y}=\mathrm{2}\:\vee\:{x}=\mathrm{2},{y}=\mathrm{3} \\ $$$$\left.\begin{matrix}{{x}+{y}=−\mathrm{7}}\\{{x}−{y}=\pm{i}\sqrt{\mathrm{23}}}\end{matrix}\right\} \\ $$$$\left.\begin{matrix}{{x}+{y}=\frac{\mathrm{70}}{\mathrm{17}}}\\{{x}−{y}=\pm\sqrt{\frac{\mathrm{376}}{\mathrm{17}}}}\end{matrix}\right\} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com