Solve the following system of equations: { ((x^3 y+x^3 y^2 +2x^2 y^2 +x^2 y^3 +xy^3 =30)),((x^2 y+xy+x+y+xy^2 =11)) :}


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 105704 by 1549442205PVT last updated on 31/Jul/20
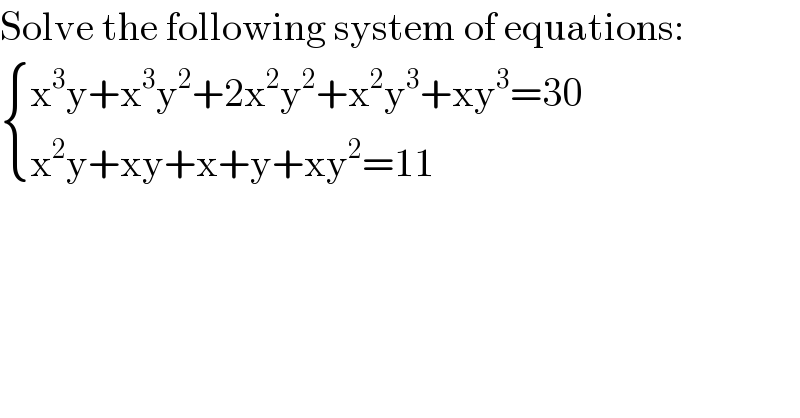
$Solve the following system of equations: { ((x^3 y+x^3 y^2 +2x^2 y^2 +x^2 y^3 +xy^3 =30)),((x^2 y+xy+x+y+xy^2 =11)) :}$
$Solve the following system of equations :$ ${\begin{cases} x^{3} y + x^{3} y^{2} + {2 x}^{2} y^{2} + x^{2} y^{3} + {xy}^{3} = 30 \\ x^{2} y + xy + x + y + {xy}^{2} = 11 \end{cases}$
Commented by PRITHWISH SEN 2 last updated on 31/Jul/20
$from eqn. (i) xy(x+y)(x+y+xy)=30.........(iii) from eqn. (ii) (xy+1)(x+y+1)=12.....(iv) now put x+y=a and xy=b then (iii)⇒ ab(a+b)=30 (iv)⇒(a+1)(b+1)=12⇒ ab+a+b=11 solving (a+b,ab)=(5,6) or (6,5) ∴ (a,b)=(5,1),(1,5),(3,2) or (2,3) for (5,1) (x,y)= {((((√7)+(√3))/2))^2 ,((((√7)−(√3))/2))^2 } and {((((√7)−(√3))/2))^2 ,((((√7)+(√3))/2))^2 } there is no real value for (a,b)=(1,5) for (3,2) (x,y)= (2,1) and (1,2) and no real value for (a,b)=(2,3)$
$from eqn . (i)$ $xy (x + y) (x + y + xy) = 30 . . . . . . . . . (iii)$ $from eqn . (ii)$ $(xy + 1) (x + y + 1) = 12 . . . . . (iv)$ $now put x + y = a and xy = b$ $then (iii) \Rightarrow ab (a + b) = 30$ $(iv) \Rightarrow (a + 1) (b + 1) = 12 \Rightarrow ab + a + b = 11$ $solving (a + b, ab) = (5, 6) or (6, 5)$ $∴ (a, b) = (5, 1), (1, 5), (3, 2) or (2, 3)$ $for (5, 1)$ $(x, y) = {{(\frac{\sqrt{7} + \sqrt{3}}{2})}^{2}, {(\frac{\sqrt{7} - \sqrt{3}}{2})}^{2}} and {{(\frac{\sqrt{7} - \sqrt{3}}{2})}^{2}, {(\frac{\sqrt{7} + \sqrt{3}}{2})}^{2}}$ $there is no real value for (a, b) = (1, 5)$ $for (3, 2)$ $(x, y) = (2, 1) and (1, 2)$ $and no real value for (a, b) = (2, 3)$
Commented by PRITHWISH SEN 2 last updated on 31/Jul/20

$welcome$
	Answered by 1549442205PVT last updated on 31/Jul/20
	$Set x+y=u,xy=v we have (1)⇔xy(x^2 +y^2 )+(xy)^2 (x+y)+2(xy)^2 =30 ⇔xy[(x+y)^2 −2xy]+(xy)^2 (x+y)+2(xy)^2 =30 (x+y)^2 (xy)+(xy)^2 (x+y)=30 (2)⇔xy(x+y)+xy+x+y=11. { ((u^2 v+v^2 u=30)),((uv+i+v=11)) :}⇔ { ((uv(u+v)=30)),((uv+u+v=11)) :} Set u+v=m,uv=n⇒ { ((m+n=11)),((mn=30)) :} ⇔(m,n)∈{(5,6),(6,5)} i)(m,n)=(5,6)⇔(u,v)∈{(3,2),(2,3)} +(u,v)=(3,2)⇔ { ((x+y=3)),((xy=2)) :}⇔(x,y)∈{(2,1),(1,2)} +(u,v)=(2,3)⇔ { ((x+y=2)),((xy=3)) :}⇒(x−y)^2 =(x+y)^2 −4xy=−8<0 This case has no roots ii)(m,n)=(6,5)⇔(u,v)∈{(5,1),(1,5)} +(u,v)=(5,1)⇔ { ((x+y=5)),((xy=1)) :}⇔ { ((x+y=5)),(((x−y)^2 =(x+y)^2 −4xy=21)) :} ⇔ { ((x+y=5)),((x−y=±(√(21)))) :} ⇔(x,y)∈{(((5+(√(21)))/2),((5−(√(21)))/2)),(((5−(√(21)))/2),((5+(√(21)))/2))} +(u,v)=(1,5)⇔ { ((x+y=1)),((xy=5)) :}⇒(x−y)^2 =(x+y)^2 −4xy=−19<0 so this case has no roots Thus,the given system has four roots: (x,y)∈{(1,2),(2,1),(((5+(√(21)))/2),((5−(√(21)))/2)),(((5−(√(21)))/2),((5+(√(21)))/2))$
	$Set x + y = u, xy = v we have$ $(1) \Leftrightarrow xy (x^{2} + y^{2}) + {(xy)}^{2} (x + y) + 2 {(xy)}^{2} = 30$ $\Leftrightarrow xy [{(x + y)}^{2} - 2 xy] + {(xy)}^{2} (x + y) + 2 {(xy)}^{2} = 30$ ${(x + y)}^{2} (xy) + {(xy)}^{2} (x + y) = 30$ $(2) \Leftrightarrow xy (x + y) + xy + x + y = 11 .$ ${\begin{cases} u^{2} v + v^{2} u = 30 \\ uv + i + v = 11 \end{cases} \Leftrightarrow {\begin{cases} uv (u + v) = 30 \\ uv + u + v = 11 \end{cases}$ $Set u + v = m, uv = n \Rightarrow {\begin{cases} m + n = 11 \\ mn = 30 \end{cases}$ $\Leftrightarrow (m, n) \in {(5, 6), (6, 5)}$ $i) (m, n) = (5, 6) \Leftrightarrow (u, v) \in {(3, 2), (2, 3)}$ $+ (u, v) = (3, 2) \Leftrightarrow {\begin{cases} x + y = 3 \\ xy = 2 \end{cases} \Leftrightarrow (x, y) \in {(2, 1), (1, 2)}$ $+ (u, v) = (2, 3) \Leftrightarrow {\begin{cases} x + y = 2 \\ xy = 3 \end{cases} \Rightarrow {(x - y)}^{2} = {(x + y)}^{2} - 4 xy = - 8 < 0$ $This case has no roots$ $ii) (m, n) = (6, 5) \Leftrightarrow (u, v) \in {(5, 1), (1, 5)}$ $+ (u, v) = (5, 1) \Leftrightarrow {\begin{cases} x + y = 5 \\ xy = 1 \end{cases} \Leftrightarrow {\begin{cases} x + y = 5 \\ {(x - y)}^{2} = {(x + y)}^{2} - 4 xy = 21 \end{cases}$ $\Leftrightarrow {\begin{cases} x + y = 5 \\ x - y = \pm \sqrt{21} \end{cases} \Leftrightarrow (x, y) \in {(\frac{5 + \sqrt{21}}{2}, \frac{5 - \sqrt{21}}{2}), (\frac{5 - \sqrt{21}}{2}, \frac{5 + \sqrt{21}}{2})}$ $+ (u, v) = (1, 5) \Leftrightarrow {\begin{cases} x + y = 1 \\ xy = 5 \end{cases} \Rightarrow {(x - y)}^{2} = {(x + y)}^{2} - 4 xy = - 19 < 0$ $so this case has no roots$ $Thus, the given system has four roots :$ $(x, y) \in {(1, 2), (2, 1), (\frac{5 + \sqrt{21}}{2}, \frac{5 - \sqrt{21}}{2}), (\frac{5 - \sqrt{21}}{2}, \frac{5 + \sqrt{21}}{2})$
	Commented by 1549442205PVT last updated on 01/Aug/20

	$Ok, excuse me . Thank you sir .$
	Commented by PRITHWISH SEN 2 last updated on 31/Jul/20

	$\frac{5 + \sqrt{21}}{2} = \frac{10 + 2 \sqrt{21}}{4} = \frac{{(\sqrt{7})}^{2} + {(\sqrt{3})}^{2} + 2 . \sqrt{7} . \sqrt{3}}{4}$ $= {(\frac{\sqrt{7} + \sqrt{3}}{2})}^{2}$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum