Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 105735 by bobhans last updated on 31/Jul/20

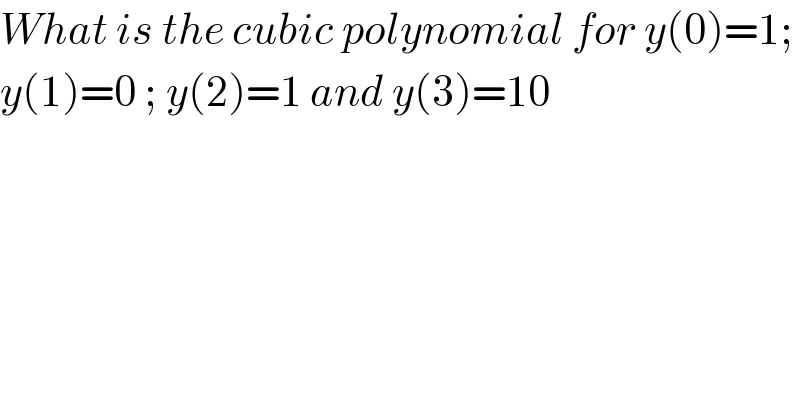
What is the cubic polynomial for y(0)=1; y(1)=0 ; y(2)=1 and y(3)=10

$${What}\:{is}\:{the}\:{cubic}\:{polynomial}\:{for}\:{y}\left(\mathrm{0}\right)=\mathrm{1}; \\ $$$${y}\left(\mathrm{1}\right)=\mathrm{0}\:;\:{y}\left(\mathrm{2}\right)=\mathrm{1}\:{and}\:{y}\left(\mathrm{3}\right)=\mathrm{10}\: \\ $$

Commented by PRITHWISH SEN 2 last updated on 31/Jul/20

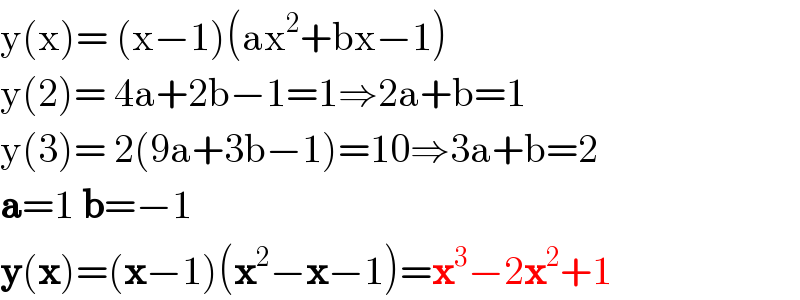
y(x)= (x−1)(ax^2 +bx−1) y(2)= 4a+2b−1=1⇒2a+b=1 y(3)= 2(9a+3b−1)=10⇒3a+b=2 a=1 b=−1 y(x)=(x−1)(x^2 −x−1)=x^3 −2x^2 +1

$$\mathrm{y}\left(\mathrm{x}\right)=\:\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{ax}^{\mathrm{2}} +\mathrm{bx}−\mathrm{1}\right) \\ $$$$\mathrm{y}\left(\mathrm{2}\right)=\:\mathrm{4a}+\mathrm{2b}−\mathrm{1}=\mathrm{1}\Rightarrow\mathrm{2a}+\mathrm{b}=\mathrm{1} \\ $$$$\mathrm{y}\left(\mathrm{3}\right)=\:\mathrm{2}\left(\mathrm{9a}+\mathrm{3b}−\mathrm{1}\right)=\mathrm{10}\Rightarrow\mathrm{3a}+\mathrm{b}=\mathrm{2} \\ $$$$\boldsymbol{\mathrm{a}}=\mathrm{1}\:\boldsymbol{\mathrm{b}}=−\mathrm{1} \\ $$$$\boldsymbol{\mathrm{y}}\left(\boldsymbol{\mathrm{x}}\right)=\left(\boldsymbol{\mathrm{x}}−\mathrm{1}\right)\left(\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\boldsymbol{\mathrm{x}}−\mathrm{1}\right)=\boldsymbol{\mathrm{x}}^{\mathrm{3}} −\mathrm{2}\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{1} \\ $$

Answered by bemath last updated on 31/Jul/20

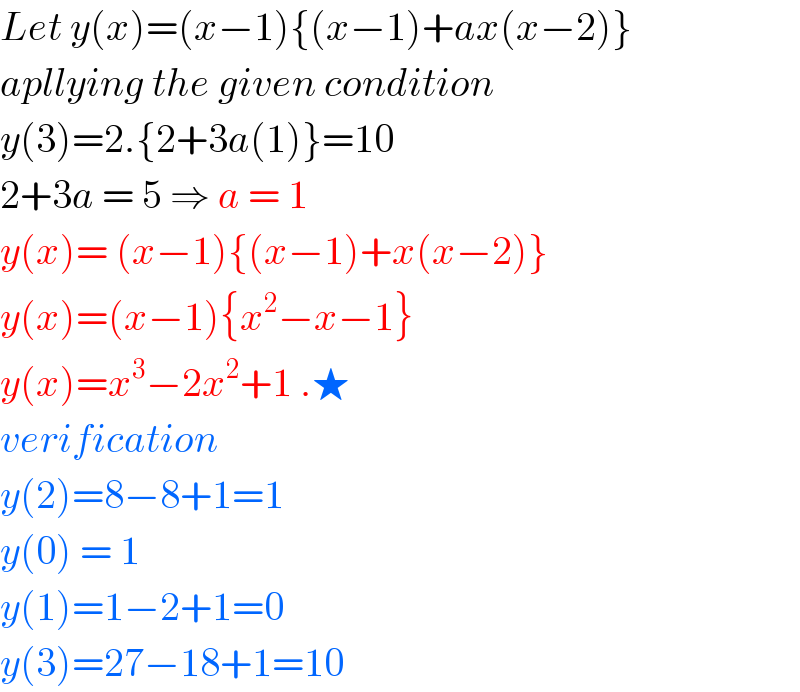
Let y(x)=(x−1){(x−1)+ax(x−2)} apllying the given condition y(3)=2.{2+3a(1)}=10 2+3a = 5 ⇒ a = 1 y(x)= (x−1){(x−1)+x(x−2)} y(x)=(x−1){x^2 −x−1} y(x)=x^3 −2x^2 +1 .★ verification y(2)=8−8+1=1 y(0) = 1 y(1)=1−2+1=0 y(3)=27−18+1=10

$${Let}\:{y}\left({x}\right)=\left({x}−\mathrm{1}\right)\left\{\left({x}−\mathrm{1}\right)+{ax}\left({x}−\mathrm{2}\right)\right\} \\ $$$${apllying}\:{the}\:{given}\:{condition}\: \\ $$$${y}\left(\mathrm{3}\right)=\mathrm{2}.\left\{\mathrm{2}+\mathrm{3}{a}\left(\mathrm{1}\right)\right\}=\mathrm{10} \\ $$$$\mathrm{2}+\mathrm{3}{a}\:=\:\mathrm{5}\:\Rightarrow\:{a}\:=\:\mathrm{1}\: \\ $$$${y}\left({x}\right)=\:\left({x}−\mathrm{1}\right)\left\{\left({x}−\mathrm{1}\right)+{x}\left({x}−\mathrm{2}\right)\right\} \\ $$$${y}\left({x}\right)=\left({x}−\mathrm{1}\right)\left\{{x}^{\mathrm{2}} −{x}−\mathrm{1}\right\} \\ $$$${y}\left({x}\right)={x}^{\mathrm{3}} −\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}\:.\bigstar \\ $$$${verification}\: \\ $$$${y}\left(\mathrm{2}\right)=\mathrm{8}−\mathrm{8}+\mathrm{1}=\mathrm{1} \\ $$$${y}\left(\mathrm{0}\right)\:=\:\mathrm{1} \\ $$$${y}\left(\mathrm{1}\right)=\mathrm{1}−\mathrm{2}+\mathrm{1}=\mathrm{0} \\ $$$${y}\left(\mathrm{3}\right)=\mathrm{27}−\mathrm{18}+\mathrm{1}=\mathrm{10}\: \\ $$

Answered by floor(10²Eta[1]) last updated on 31/Jul/20

y(0)=1⇒y(x)=a(x)(x)+1 y(1)=a(1)+1=0⇒a(1)=−1 ⇒a(x)=b(x)(x−1)−1 ⇒y(x)=[b(x)(x−1)−1]x+1 y(2)=[b(2)−1].2+1=1⇒b(2)=1 ⇒b(x)=c(x)(x−2)+1 ⇒y(x)=[[c(x)(x−2)+1].(x−1)−1]x+1 y(3)=[[c(3)+1].2−1].3+1=10⇒c(3)=1 ⇒c(x)=1 (constant bc y(x) is cubic) ⇒y(x)=[(x−1)(x−1)−1].x+1 y(x)=[x^2 −2x].x+1 ⇒y(x)=x^3 −2x^2 +1

$$\mathrm{y}\left(\mathrm{0}\right)=\mathrm{1}\Rightarrow\mathrm{y}\left(\mathrm{x}\right)=\mathrm{a}\left(\mathrm{x}\right)\left(\mathrm{x}\right)+\mathrm{1} \\ $$$$\mathrm{y}\left(\mathrm{1}\right)=\mathrm{a}\left(\mathrm{1}\right)+\mathrm{1}=\mathrm{0}\Rightarrow\mathrm{a}\left(\mathrm{1}\right)=−\mathrm{1} \\ $$$$\Rightarrow\mathrm{a}\left(\mathrm{x}\right)=\mathrm{b}\left(\mathrm{x}\right)\left(\mathrm{x}−\mathrm{1}\right)−\mathrm{1} \\ $$$$\Rightarrow\mathrm{y}\left(\mathrm{x}\right)=\left[\mathrm{b}\left(\mathrm{x}\right)\left(\mathrm{x}−\mathrm{1}\right)−\mathrm{1}\right]\mathrm{x}+\mathrm{1} \\ $$$$\mathrm{y}\left(\mathrm{2}\right)=\left[\mathrm{b}\left(\mathrm{2}\right)−\mathrm{1}\right].\mathrm{2}+\mathrm{1}=\mathrm{1}\Rightarrow\mathrm{b}\left(\mathrm{2}\right)=\mathrm{1} \\ $$$$\Rightarrow\mathrm{b}\left(\mathrm{x}\right)=\mathrm{c}\left(\mathrm{x}\right)\left(\mathrm{x}−\mathrm{2}\right)+\mathrm{1} \\ $$$$\Rightarrow\mathrm{y}\left(\mathrm{x}\right)=\left[\left[\mathrm{c}\left(\mathrm{x}\right)\left(\mathrm{x}−\mathrm{2}\right)+\mathrm{1}\right].\left(\mathrm{x}−\mathrm{1}\right)−\mathrm{1}\right]\mathrm{x}+\mathrm{1} \\ $$$$\mathrm{y}\left(\mathrm{3}\right)=\left[\left[\mathrm{c}\left(\mathrm{3}\right)+\mathrm{1}\right].\mathrm{2}−\mathrm{1}\right].\mathrm{3}+\mathrm{1}=\mathrm{10}\Rightarrow\mathrm{c}\left(\mathrm{3}\right)=\mathrm{1} \\ $$$$\Rightarrow\mathrm{c}\left(\mathrm{x}\right)=\mathrm{1}\:\left(\mathrm{constant}\:\mathrm{bc}\:\mathrm{y}\left(\mathrm{x}\right)\:\mathrm{is}\:\mathrm{cubic}\right) \\ $$$$\Rightarrow\mathrm{y}\left(\mathrm{x}\right)=\left[\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}−\mathrm{1}\right)−\mathrm{1}\right].\mathrm{x}+\mathrm{1} \\ $$$$\mathrm{y}\left(\mathrm{x}\right)=\left[\mathrm{x}^{\mathrm{2}} −\mathrm{2x}\right].\mathrm{x}+\mathrm{1} \\ $$$$\Rightarrow\mathrm{y}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{3}} −\mathrm{2x}^{\mathrm{2}} +\mathrm{1} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com