
Question and Answers Forum
Question Number 105940 by Dwaipayan Shikari last updated on 01/Aug/20
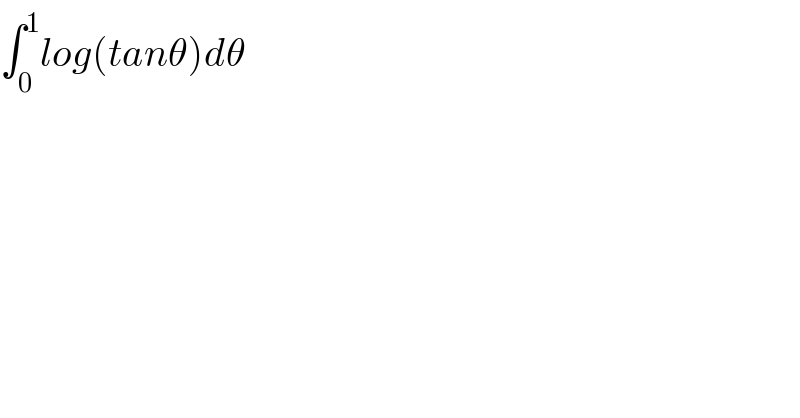
Answered by mathmax by abdo last updated on 01/Aug/20
![A =∫_0 ^1 ln(tanθ)dθ by parts A = [θln(tanθ)]_0 ^1 −∫_0 ^1 θ×((1+tan^2 θ)/(tanθ)) dθ =ln((π/4))−∫_0 ^1 θ{(1/(tanθ)) +tanθ}dθ changement tanθ =x give ∫_0 ^1 θ{(1/(tanθ)) +tanθ }dθ =∫_0 ^(tan(1)) arctanx{(1/x) +x}(dx/(1+x^2 )) =∫_0 ^(tan(1)) ((1+x^2 )/x) ×((arctanx)/(1+x^2 ))dx =∫_0 ^(tan(1)) ((arctan(x))/x)dx let f(a) =∫_0 ^(tan(1)) ((arctan(αx))/x)dx ⇒f^′ (a) =∫_0 ^(tan(1)) (x/((1+α^2 x^2 )x))dx =∫_0 ^(tan(1)) (dx/(1+α^2 x^2 )) =_(αx =z) ∫_0 ^(αtan(1)) (dz/(α(1+z^2 ))) =(1/α)[arctanz]_0 ^(αtan(1)) =((arctan(αtan(1)))/α) ⇒f(α) =∫_0 ^α ((arctan(utan(1)))/u) du + C and ∫_0 ^(tan(1)) ((arctanx)/x)dx =f(1) =∫_0 ^1 ((arctan(utan(1)))/u) du +C ..be continued...](Q105954.png)
| ||
Question and Answers Forum | ||
Question Number 105940 by Dwaipayan Shikari last updated on 01/Aug/20 | ||
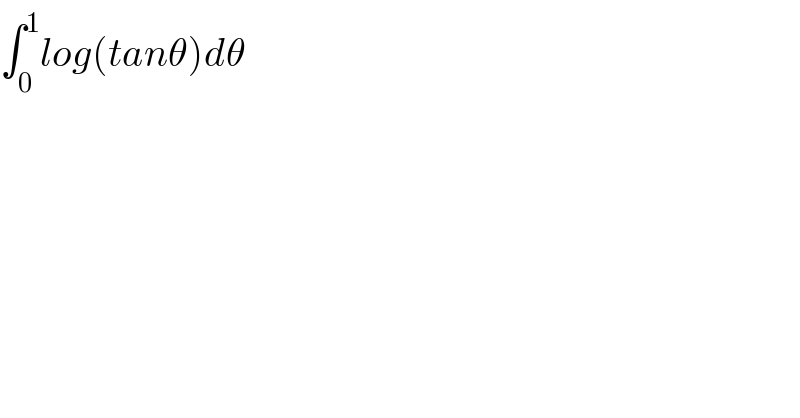 | ||
Answered by mathmax by abdo last updated on 01/Aug/20 | ||
![A =∫_0 ^1 ln(tanθ)dθ by parts A = [θln(tanθ)]_0 ^1 −∫_0 ^1 θ×((1+tan^2 θ)/(tanθ)) dθ =ln((π/4))−∫_0 ^1 θ{(1/(tanθ)) +tanθ}dθ changement tanθ =x give ∫_0 ^1 θ{(1/(tanθ)) +tanθ }dθ =∫_0 ^(tan(1)) arctanx{(1/x) +x}(dx/(1+x^2 )) =∫_0 ^(tan(1)) ((1+x^2 )/x) ×((arctanx)/(1+x^2 ))dx =∫_0 ^(tan(1)) ((arctan(x))/x)dx let f(a) =∫_0 ^(tan(1)) ((arctan(αx))/x)dx ⇒f^′ (a) =∫_0 ^(tan(1)) (x/((1+α^2 x^2 )x))dx =∫_0 ^(tan(1)) (dx/(1+α^2 x^2 )) =_(αx =z) ∫_0 ^(αtan(1)) (dz/(α(1+z^2 ))) =(1/α)[arctanz]_0 ^(αtan(1)) =((arctan(αtan(1)))/α) ⇒f(α) =∫_0 ^α ((arctan(utan(1)))/u) du + C and ∫_0 ^(tan(1)) ((arctanx)/x)dx =f(1) =∫_0 ^1 ((arctan(utan(1)))/u) du +C ..be continued...](Q105954.png) | ||
| ||