Question and Answers Forum
Question Number 106222 by Rasheed.Sindhi last updated on 03/Aug/20
Commented byRasheed.Sindhi last updated on 03/Aug/20
Thanks sir 〽️�� ��
Commented byRasheed.Sindhi last updated on 03/Aug/20
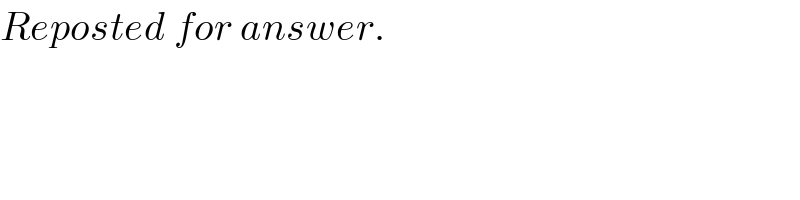
Commented bymr W last updated on 03/Aug/20
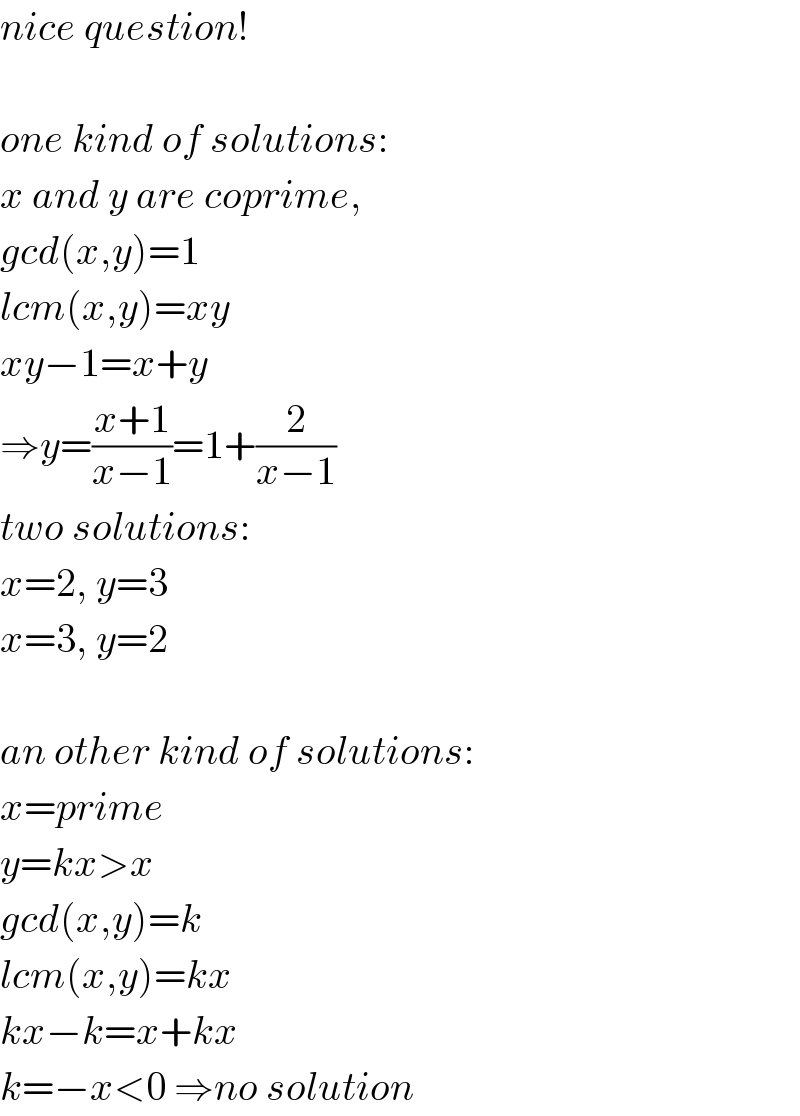
Commented byRasheed.Sindhi last updated on 03/Aug/20
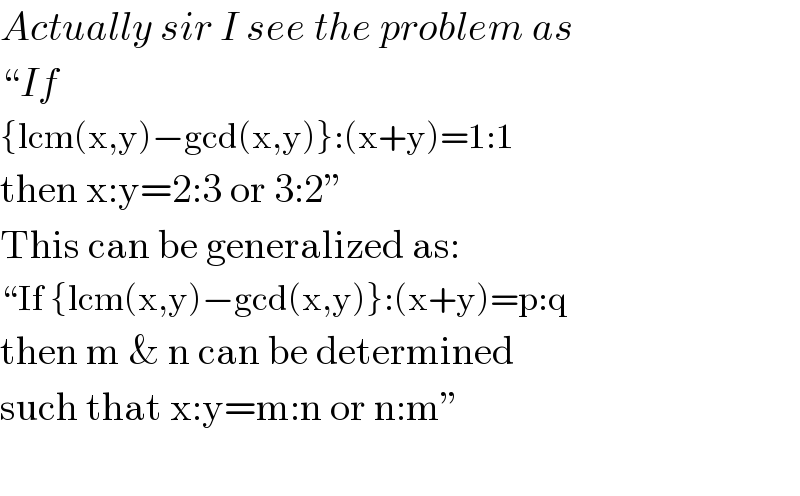
Commented bymr W last updated on 03/Aug/20

Answered by Rasheed.Sindhi last updated on 03/Aug/20
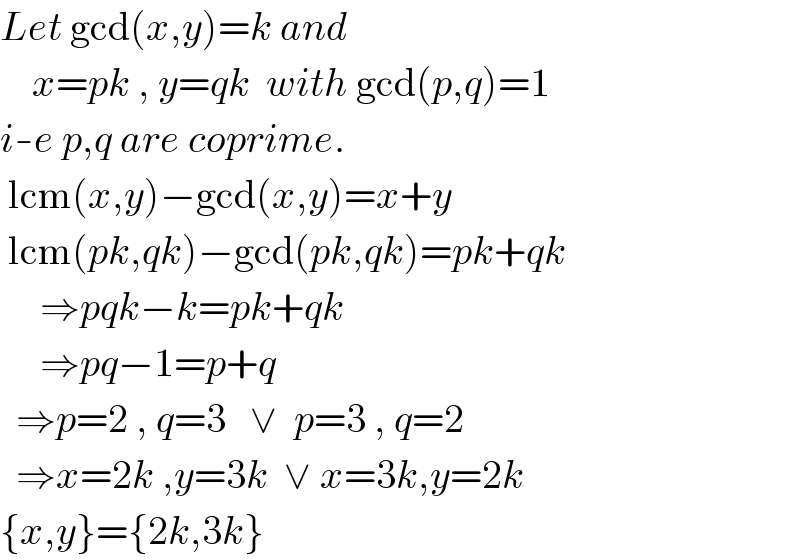
Commented byRasheed.Sindhi last updated on 03/Aug/20
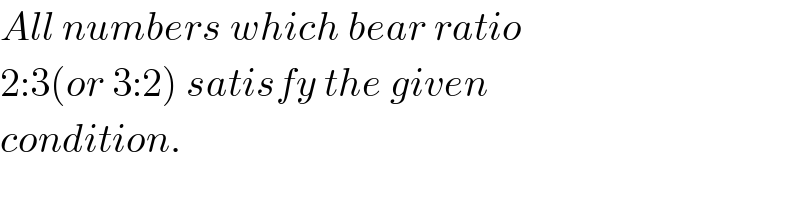
Commented byRasheed.Sindhi last updated on 03/Aug/20
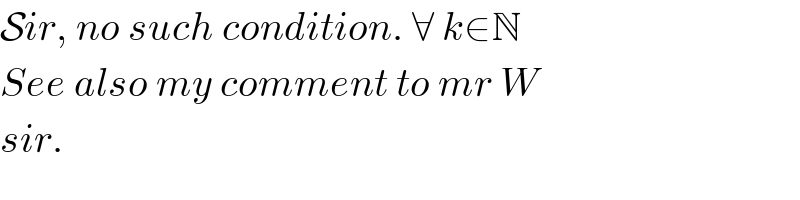
Commented byRasheed.Sindhi last updated on 03/Aug/20
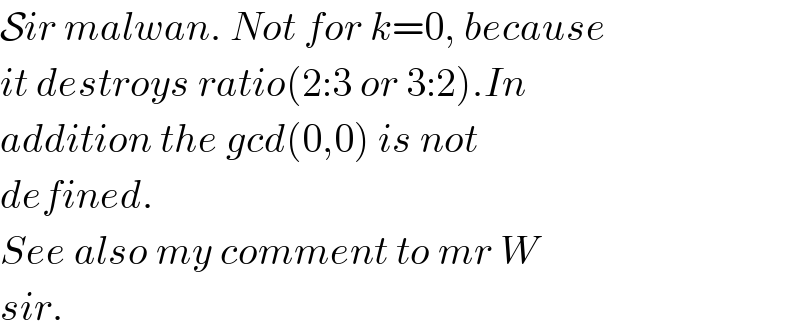
Commented byPRITHWISH SEN 2 last updated on 03/Aug/20

Commented bymalwaan last updated on 03/Aug/20
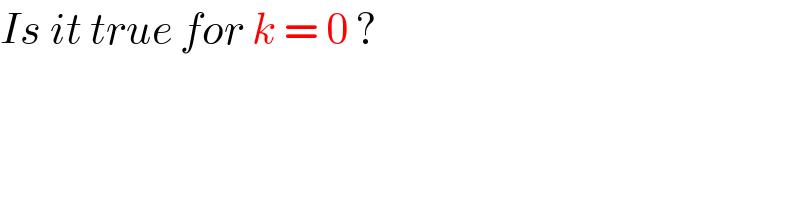
Commented byPRITHWISH SEN 2 last updated on 03/Aug/20

Commented bymalwaan last updated on 04/Aug/20