Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 106120 by Her_Majesty last updated on 02/Aug/20

question 106075 again ∫((1+cosx)/((99cosx−70sinx+210)cosx−66sinx+110))dx=? using t=tan(x/2) I get −4∫(dt/(t^4 +8t^3 −22t^2 +272t−419)) can someone factorize the denominator?

$${question}\:\mathrm{106075}\:{again} \\ $$$$\int\frac{\mathrm{1}+{cosx}}{\left(\mathrm{99}{cosx}−\mathrm{70}{sinx}+\mathrm{210}\right){cosx}−\mathrm{66}{sinx}+\mathrm{110}}{dx}=? \\ $$$${using}\:{t}={tan}\left({x}/\mathrm{2}\right)\:{I}\:{get} \\ $$$$−\mathrm{4}\int\frac{{dt}}{{t}^{\mathrm{4}} +\mathrm{8}{t}^{\mathrm{3}} −\mathrm{22}{t}^{\mathrm{2}} +\mathrm{272}{t}−\mathrm{419}} \\ $$$${can}\:{someone}\:{factorize}\:{the}\:{denominator}? \\ $$

Commented by Sarah85 last updated on 03/Aug/20

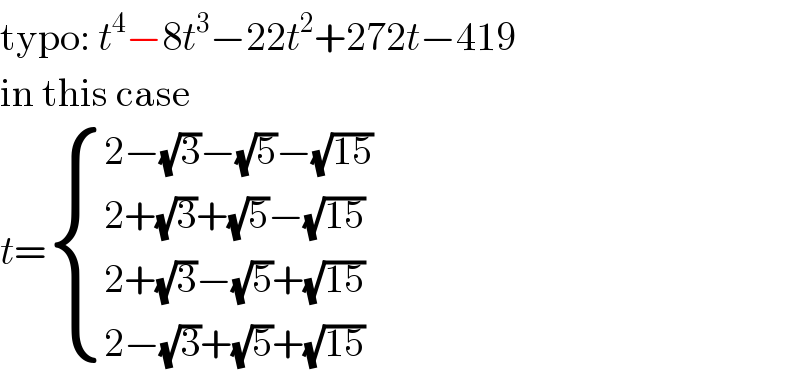
typo: t^4 −8t^3 −22t^2 +272t−419 in this case t= { ((2−(√3)−(√5)−(√(15)))),((2+(√3)+(√5)−(√(15)))),((2+(√3)−(√5)+(√(15)))),((2−(√3)+(√5)+(√(15)))) :}

$$\mathrm{typo}:\:{t}^{\mathrm{4}} −\mathrm{8}{t}^{\mathrm{3}} −\mathrm{22}{t}^{\mathrm{2}} +\mathrm{272}{t}−\mathrm{419} \\ $$$$\mathrm{in}\:\mathrm{this}\:\mathrm{case} \\ $$$${t}=\begin{cases}{\mathrm{2}−\sqrt{\mathrm{3}}−\sqrt{\mathrm{5}}−\sqrt{\mathrm{15}}}\\{\mathrm{2}+\sqrt{\mathrm{3}}+\sqrt{\mathrm{5}}−\sqrt{\mathrm{15}}}\\{\mathrm{2}+\sqrt{\mathrm{3}}−\sqrt{\mathrm{5}}+\sqrt{\mathrm{15}}}\\{\mathrm{2}−\sqrt{\mathrm{3}}+\sqrt{\mathrm{5}}+\sqrt{\mathrm{15}}}\end{cases} \\ $$

Commented by Her_Majesty last updated on 03/Aug/20

thanks but how you got it?

$${thanks}\:{but}\:{how}\:{you}\:{got}\:{it}? \\ $$

Commented by 1549442205PVT last updated on 03/Aug/20

t^4 −8t^3 −22t^2 +272t−419=0 ⇔[t^2 −(4−2(√(15)))t+11−6(√(15)) ]× [t^2 −(4+2(√(15)))t+11+6(√(15))]=0 ⇔[t^2 −(4−2(√5))t−(9+10(√5))]× [t^2 −(4+2(√5))t−(9−10(√5))]=0

$$\mathrm{t}^{\mathrm{4}} −\mathrm{8t}^{\mathrm{3}} −\mathrm{22t}^{\mathrm{2}} +\mathrm{272t}−\mathrm{419}=\mathrm{0} \\ $$$$\Leftrightarrow\left[\boldsymbol{\mathrm{t}}^{\mathrm{2}} −\left(\mathrm{4}−\mathrm{2}\sqrt{\mathrm{15}}\right)\boldsymbol{\mathrm{t}}+\mathrm{11}−\mathrm{6}\sqrt{\mathrm{15}}\:\right]× \\ $$$$\left[\boldsymbol{\mathrm{t}}^{\mathrm{2}} −\left(\mathrm{4}+\mathrm{2}\sqrt{\mathrm{15}}\right)\boldsymbol{\mathrm{t}}+\mathrm{11}+\mathrm{6}\sqrt{\mathrm{15}}\right]=\mathrm{0} \\ $$$$\Leftrightarrow\left[\boldsymbol{\mathrm{t}}^{\mathrm{2}} −\left(\mathrm{4}−\mathrm{2}\sqrt{\mathrm{5}}\right)\boldsymbol{\mathrm{t}}−\left(\mathrm{9}+\mathrm{10}\sqrt{\mathrm{5}}\right)\right]× \\ $$$$\left[\boldsymbol{\mathrm{t}}^{\mathrm{2}} −\left(\mathrm{4}+\mathrm{2}\sqrt{\mathrm{5}}\right)\boldsymbol{\mathrm{t}}−\left(\mathrm{9}−\mathrm{10}\sqrt{\mathrm{5}}\right)\right]=\mathrm{0} \\ $$

Answered by 1549442205PVT last updated on 03/Aug/20

t^4 +8t^3 −22t^2 +272t−419 =(t^2 +10.374065851t−19.19728528)× (t^2 −2.374065851+21.82600076) two real roots be x_1 =1.602856312,x_2 =−11.97692216

$${t}^{\mathrm{4}} +\mathrm{8}{t}^{\mathrm{3}} −\mathrm{22}{t}^{\mathrm{2}} +\mathrm{272}{t}−\mathrm{419} \\ $$$$=\left(\mathrm{t}^{\mathrm{2}} +\mathrm{10}.\mathrm{374065851t}−\mathrm{19}.\mathrm{19728528}\right)× \\ $$$$\left(\mathrm{t}^{\mathrm{2}} −\mathrm{2}.\mathrm{374065851}+\mathrm{21}.\mathrm{82600076}\right) \\ $$$$\mathrm{two}\:\mathrm{real}\:\mathrm{roots}\:\mathrm{be} \\ $$$$\mathrm{x}_{\mathrm{1}} =\mathrm{1}.\mathrm{602856312},\mathrm{x}_{\mathrm{2}} =−\mathrm{11}.\mathrm{97692216} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com