Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 106133 by mathmax by abdo last updated on 02/Aug/20

let f(x) =e^(−2x) ln(3−x^2 ) 1) calculate f^((n)) (x)and f^((n)) (0) 2) developp f at integr serie

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{e}^{−\mathrm{2x}} \mathrm{ln}\left(\mathrm{3}−\mathrm{x}^{\mathrm{2}} \right) \\ $$$$\left.\mathrm{1}\right)\:\mathrm{calculate}\:\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{x}\right)\mathrm{and}\:\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{0}\right) \\ $$$$\left.\mathrm{2}\right)\:\mathrm{developp}\:\mathrm{f}\:\mathrm{at}\:\mathrm{integr}\:\mathrm{serie} \\ $$

Answered by mathmax by abdo last updated on 03/Aug/20

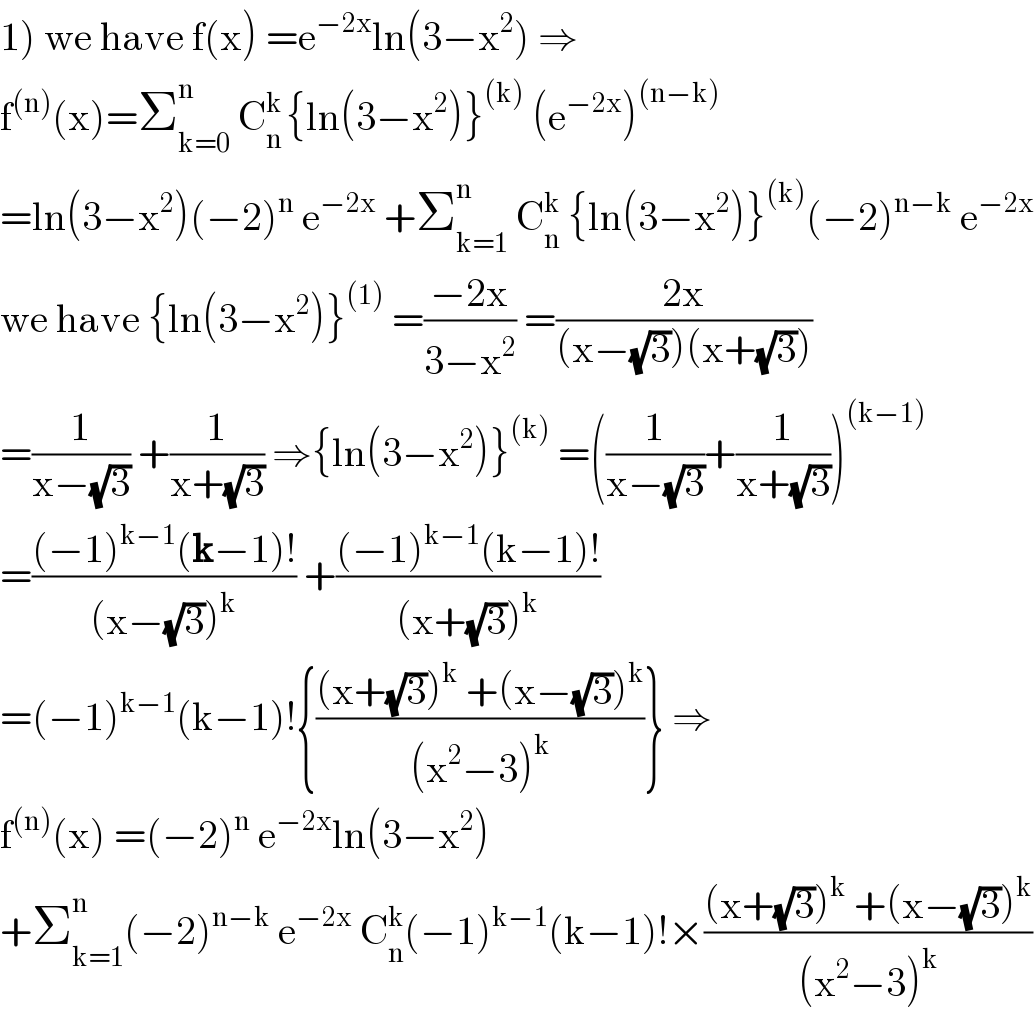
1) we have f(x) =e^(−2x) ln(3−x^2 ) ⇒ f^((n)) (x)=Σ_(k=0) ^n C_n ^(k ) {ln(3−x^2 )}^((k)) (e^(−2x) )^((n−k)) =ln(3−x^2 )(−2)^n e^(−2x) +Σ_(k=1) ^n C_n ^k {ln(3−x^2 )}^((k)) (−2)^(n−k) e^(−2x) we have {ln(3−x^2 )}^((1)) =((−2x)/(3−x^2 )) =((2x)/((x−(√3))(x+(√3)))) =(1/(x−(√3))) +(1/(x+(√3))) ⇒{ln(3−x^2 )}^((k)) =((1/(x−(√3)))+(1/(x+(√3))))^((k−1)) =(((−1)^(k−1) (k−1)!)/((x−(√3))^k )) +(((−1)^(k−1) (k−1)!)/((x+(√3))^k )) =(−1)^(k−1) (k−1)!{(((x+(√3))^k +(x−(√3))^k )/((x^2 −3)^k ))} ⇒ f^((n)) (x) =(−2)^n e^(−2x) ln(3−x^2 ) +Σ_(k=1) ^(n ) (−2)^(n−k) e^(−2x) C_n ^k (−1)^(k−1) (k−1)!×(((x+(√3))^k +(x−(√3))^k )/((x^2 −3)^k ))

$$\left.\mathrm{1}\right)\:\mathrm{we}\:\mathrm{have}\:\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{e}^{−\mathrm{2x}} \mathrm{ln}\left(\mathrm{3}−\mathrm{x}^{\mathrm{2}} \right)\:\Rightarrow \\ $$$$\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{x}\right)=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}\:} \left\{\mathrm{ln}\left(\mathrm{3}−\mathrm{x}^{\mathrm{2}} \right)\right\}^{\left(\mathrm{k}\right)} \:\left(\mathrm{e}^{−\mathrm{2x}} \right)^{\left(\mathrm{n}−\mathrm{k}\right)} \\ $$$$=\mathrm{ln}\left(\mathrm{3}−\mathrm{x}^{\mathrm{2}} \right)\left(−\mathrm{2}\right)^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{2x}} \:+\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\left\{\mathrm{ln}\left(\mathrm{3}−\mathrm{x}^{\mathrm{2}} \right)\right\}^{\left(\mathrm{k}\right)} \left(−\mathrm{2}\right)^{\mathrm{n}−\mathrm{k}} \:\mathrm{e}^{−\mathrm{2x}} \\ $$$$\mathrm{we}\:\mathrm{have}\:\left\{\mathrm{ln}\left(\mathrm{3}−\mathrm{x}^{\mathrm{2}} \right)\right\}^{\left(\mathrm{1}\right)} \:=\frac{−\mathrm{2x}}{\mathrm{3}−\mathrm{x}^{\mathrm{2}} }\:=\frac{\mathrm{2x}}{\left(\mathrm{x}−\sqrt{\mathrm{3}}\right)\left(\mathrm{x}+\sqrt{\mathrm{3}}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{x}−\sqrt{\mathrm{3}}}\:+\frac{\mathrm{1}}{\mathrm{x}+\sqrt{\mathrm{3}}}\:\Rightarrow\left\{\mathrm{ln}\left(\mathrm{3}−\mathrm{x}^{\mathrm{2}} \right)\right\}^{\left(\mathrm{k}\right)} \:=\left(\frac{\mathrm{1}}{\mathrm{x}−\sqrt{\mathrm{3}}}+\frac{\mathrm{1}}{\mathrm{x}+\sqrt{\mathrm{3}}}\right)^{\left(\mathrm{k}−\mathrm{1}\right)} \\ $$$$=\frac{\left(−\mathrm{1}\right)^{\mathrm{k}−\mathrm{1}} \left(\boldsymbol{\mathrm{k}}−\mathrm{1}\right)!}{\left(\mathrm{x}−\sqrt{\mathrm{3}}\right)^{\mathrm{k}} }\:+\frac{\left(−\mathrm{1}\right)^{\mathrm{k}−\mathrm{1}} \left(\mathrm{k}−\mathrm{1}\right)!}{\left(\mathrm{x}+\sqrt{\mathrm{3}}\right)^{\mathrm{k}} } \\ $$$$=\left(−\mathrm{1}\right)^{\mathrm{k}−\mathrm{1}} \left(\mathrm{k}−\mathrm{1}\right)!\left\{\frac{\left(\mathrm{x}+\sqrt{\mathrm{3}}\right)^{\mathrm{k}} \:+\left(\mathrm{x}−\sqrt{\mathrm{3}}\right)^{\mathrm{k}} }{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{3}\right)^{\mathrm{k}} }\right\}\:\Rightarrow \\ $$$$\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{x}\right)\:=\left(−\mathrm{2}\right)^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{2x}} \mathrm{ln}\left(\mathrm{3}−\mathrm{x}^{\mathrm{2}} \right) \\ $$$$+\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}\:} \left(−\mathrm{2}\right)^{\mathrm{n}−\mathrm{k}} \:\mathrm{e}^{−\mathrm{2x}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \left(−\mathrm{1}\right)^{\mathrm{k}−\mathrm{1}} \left(\mathrm{k}−\mathrm{1}\right)!×\frac{\left(\mathrm{x}+\sqrt{\mathrm{3}}\right)^{\mathrm{k}} \:+\left(\mathrm{x}−\sqrt{\mathrm{3}}\right)^{\mathrm{k}} }{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{3}\right)^{\mathrm{k}} } \\ $$

Commented by mathmax by abdo last updated on 03/Aug/20

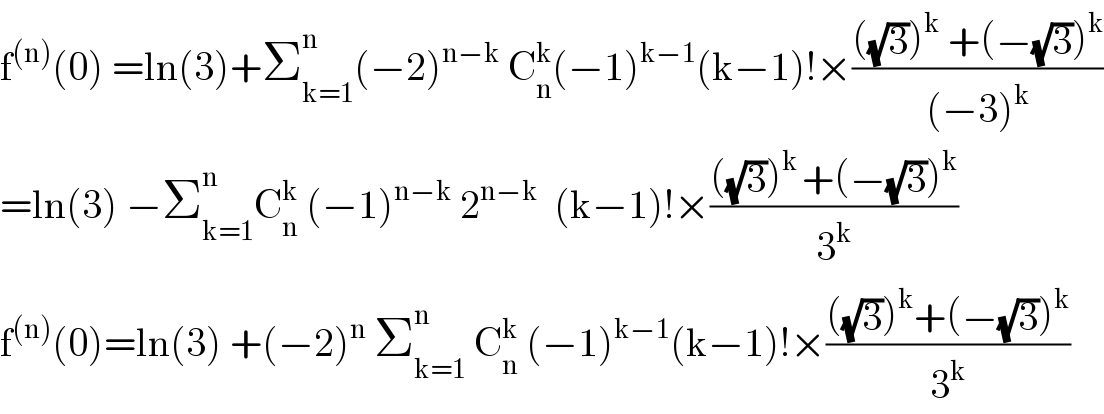
f^((n)) (0) =ln(3)+Σ_(k=1) ^n (−2)^(n−k) C_n ^k (−1)^(k−1) (k−1)!×((((√3))^k +(−(√3))^k )/((−3)^k )) =ln(3) −Σ_(k=1) ^n C_n ^k (−1)^(n−k) 2^(n−k) (k−1)!×((((√3))^(k ) +(−(√3))^k )/3^k ) f^((n)) (0)=ln(3) +(−2)^n Σ_(k=1) ^n C_n ^k (−1)^(k−1) (k−1)!×((((√3))^k +(−(√3))^k )/3^k )

$$\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{0}\right)\:=\mathrm{ln}\left(\mathrm{3}\right)+\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \left(−\mathrm{2}\right)^{\mathrm{n}−\mathrm{k}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \left(−\mathrm{1}\right)^{\mathrm{k}−\mathrm{1}} \left(\mathrm{k}−\mathrm{1}\right)!×\frac{\left(\sqrt{\mathrm{3}}\right)^{\mathrm{k}} \:+\left(−\sqrt{\mathrm{3}}\right)^{\mathrm{k}} }{\left(−\mathrm{3}\right)^{\mathrm{k}} } \\ $$$$=\mathrm{ln}\left(\mathrm{3}\right)\:−\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{k}} \:\mathrm{2}^{\mathrm{n}−\mathrm{k}} \:\:\left(\mathrm{k}−\mathrm{1}\right)!×\frac{\left(\sqrt{\mathrm{3}}\right)^{\mathrm{k}\:} +\left(−\sqrt{\mathrm{3}}\right)^{\mathrm{k}} }{\mathrm{3}^{\mathrm{k}} } \\ $$$$\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{0}\right)=\mathrm{ln}\left(\mathrm{3}\right)\:+\left(−\mathrm{2}\right)^{\mathrm{n}} \:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\left(−\mathrm{1}\right)^{\mathrm{k}−\mathrm{1}} \left(\mathrm{k}−\mathrm{1}\right)!×\frac{\left(\sqrt{\mathrm{3}}\right)^{\mathrm{k}} +\left(−\sqrt{\mathrm{3}}\right)^{\mathrm{k}} }{\mathrm{3}^{\mathrm{k}} } \\ $$

Commented by mathmax by abdo last updated on 03/Aug/20

2)f(x) =Σ_(n=0) ^∞ ((f^((n)) (o))/(n!)) x^n =ln(3) +Σ_(n=1) ^∞ (1/(n!)){ln(3)+(−2)^n Σ_(k=1) ^n C_n ^k (−1)^(k−1) (k−1)!×((((√3))^k +(−(√3))^k )/3^k )}x^n =ln(3)e^(x ) +Σ_(n=1) ^∞ {(−2)^n Σ_(p=1) ^([(n/2)] ) C_n ^(2p) (−1)(2p−1)!×((2.3^p )/3^(2p) )}x^n f(x)=ln(3)e^x +Σ_(n=1) ^∞ (−2)^(n+1) { Σ_(p=1) ^([(n/2)]) C_n ^(2p) (((2p−1))/3^p )}x^n

$$\left.\mathrm{2}\right)\mathrm{f}\left(\mathrm{x}\right)\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{o}\right)}{\mathrm{n}!}\:\mathrm{x}^{\mathrm{n}} \:=\mathrm{ln}\left(\mathrm{3}\right) \\ $$$$+\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \frac{\mathrm{1}}{\mathrm{n}!}\left\{\mathrm{ln}\left(\mathrm{3}\right)+\left(−\mathrm{2}\right)^{\mathrm{n}} \:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \left(−\mathrm{1}\right)^{\mathrm{k}−\mathrm{1}} \left(\mathrm{k}−\mathrm{1}\right)!×\frac{\left(\sqrt{\mathrm{3}}\right)^{\mathrm{k}} \:+\left(−\sqrt{\mathrm{3}}\right)^{\mathrm{k}} }{\mathrm{3}^{\mathrm{k}} }\right\}\mathrm{x}^{\mathrm{n}} \\ $$$$=\mathrm{ln}\left(\mathrm{3}\right)\mathrm{e}^{\mathrm{x}\:} \:+\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\left\{\left(−\mathrm{2}\right)^{\mathrm{n}} \:\sum_{\mathrm{p}=\mathrm{1}} ^{\left[\frac{\mathrm{n}}{\mathrm{2}}\right]\:} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{2p}} \:\left(−\mathrm{1}\right)\left(\mathrm{2p}−\mathrm{1}\right)!×\frac{\mathrm{2}.\mathrm{3}^{\mathrm{p}} }{\mathrm{3}^{\mathrm{2p}} }\right\}\mathrm{x}^{\mathrm{n}} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{ln}\left(\mathrm{3}\right)\mathrm{e}^{\mathrm{x}} \:+\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\left(−\mathrm{2}\right)^{\mathrm{n}+\mathrm{1}} \left\{\:\sum_{\mathrm{p}=\mathrm{1}} ^{\left[\frac{\mathrm{n}}{\mathrm{2}}\right]} \:\:\mathrm{C}_{\mathrm{n}} ^{\mathrm{2p}} \:\frac{\left(\mathrm{2p}−\mathrm{1}\right)}{\mathrm{3}^{\mathrm{p}} }\right\}\mathrm{x}^{\mathrm{n}} \\ $$

Commented by abdomathmax last updated on 03/Aug/20

f(x)=ln(3)Σ_(n=0) ^∞ (x^n /(n!)) +Σ_(n=1) ^∞ (−2)^(n+1) {Σ_(p=1) ^([(n/2)] ) C_n ^(2p) (((2p−1)!)/3^p )}x^n

$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{ln}\left(\mathrm{3}\right)\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}!} \\ $$$$+\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \left(−\mathrm{2}\right)^{\mathrm{n}+\mathrm{1}} \left\{\sum_{\mathrm{p}=\mathrm{1}} ^{\left[\frac{\mathrm{n}}{\mathrm{2}}\right]\:} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{2p}} \:\frac{\left(\mathrm{2p}−\mathrm{1}\right)!}{\mathrm{3}^{\mathrm{p}} }\right\}\mathrm{x}^{\mathrm{n}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com