
Question and Answers Forum
Question Number 106173 by john santu last updated on 03/Aug/20
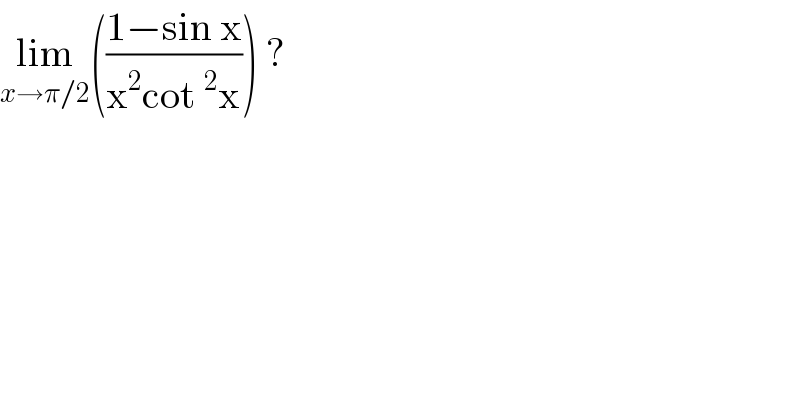
Answered by bemath last updated on 03/Aug/20
![set x = (π/2)+♭ →(4/π^2 )×lim_(♭→0) ((1−sin ((π/2)+♭))/(cot^2 ((π/2)+♭)))= (4/π^2 )×lim_(♭→0) ((1−cos ♭)/(tan^2 ♭)) = (4/π^2 )×lim_(♭→0) ((2sin^2 ((♭/2)))/(tan^2 ♭)) = (8/π^2 )×[lim_(♭→0) ((sin ((♭/2)))/(tan ♭)) ]^2 = (8/π^2 )×(1/4)=(2/π^2 ) ★](Q106174.png)
Answered by mathmax by abdo last updated on 03/Aug/20
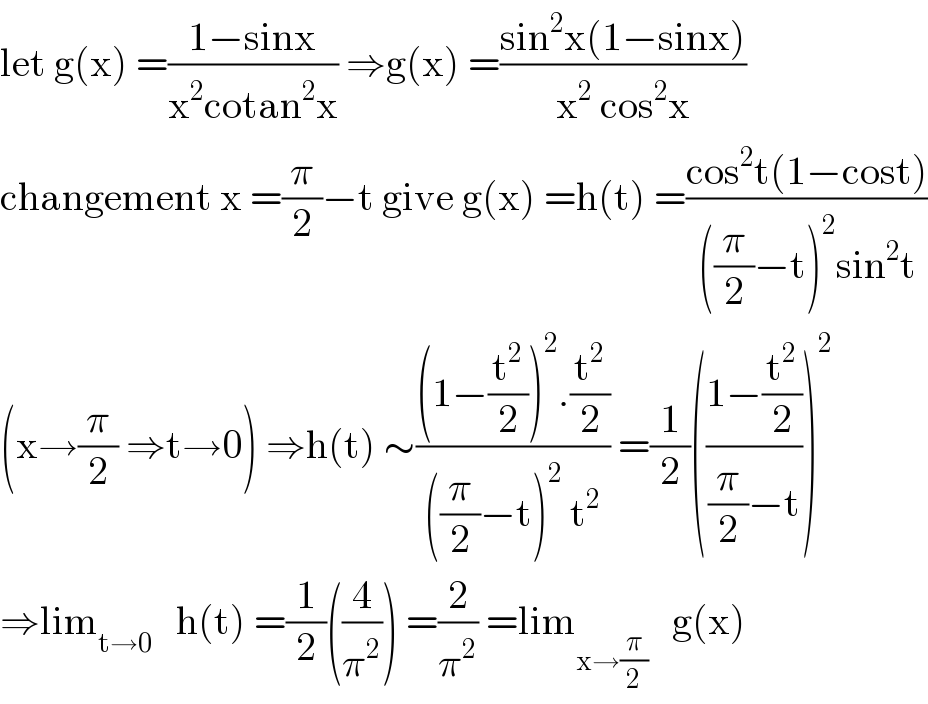
| ||
Question and Answers Forum | ||
Question Number 106173 by john santu last updated on 03/Aug/20 | ||
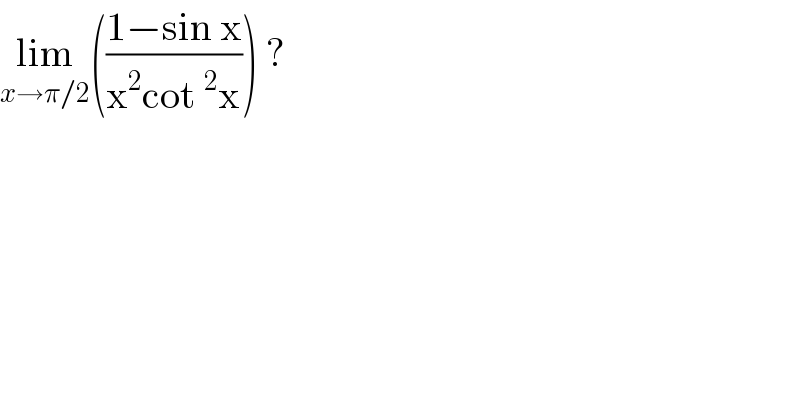 | ||
Answered by bemath last updated on 03/Aug/20 | ||
![set x = (π/2)+♭ →(4/π^2 )×lim_(♭→0) ((1−sin ((π/2)+♭))/(cot^2 ((π/2)+♭)))= (4/π^2 )×lim_(♭→0) ((1−cos ♭)/(tan^2 ♭)) = (4/π^2 )×lim_(♭→0) ((2sin^2 ((♭/2)))/(tan^2 ♭)) = (8/π^2 )×[lim_(♭→0) ((sin ((♭/2)))/(tan ♭)) ]^2 = (8/π^2 )×(1/4)=(2/π^2 ) ★](Q106174.png) | ||
| ||
Answered by mathmax by abdo last updated on 03/Aug/20 | ||
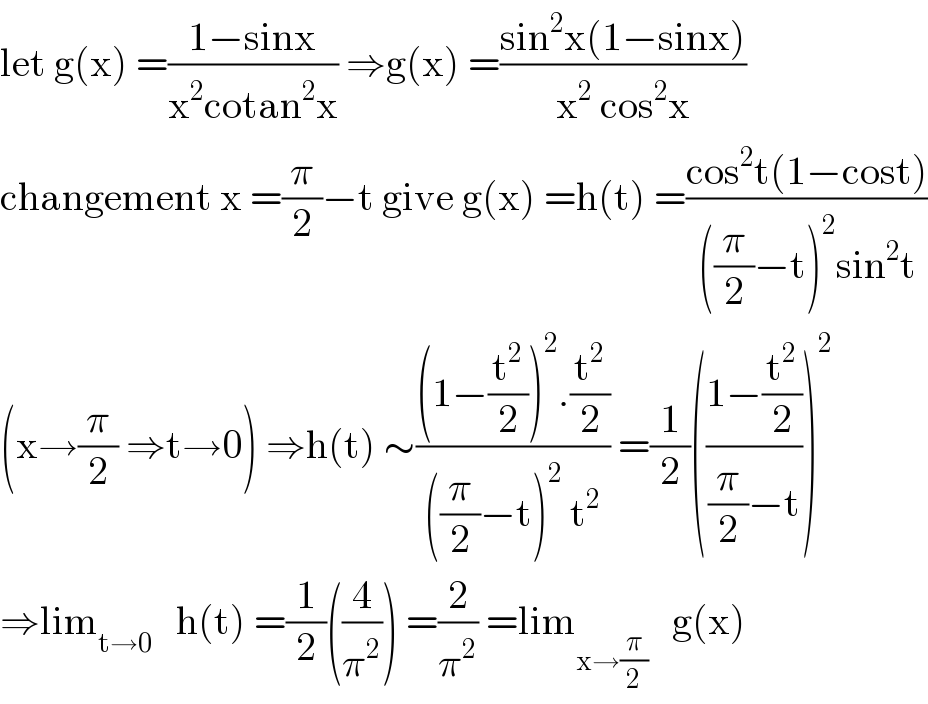 | ||
| ||