Solve for x x^x^(...x^a ) =a with a∈R^+


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 106188 by mr W last updated on 03/Aug/20

$S o l v e f o r x$ $x^{x^{. . . x^{a}}} = a w i t h a \in R^{+}$
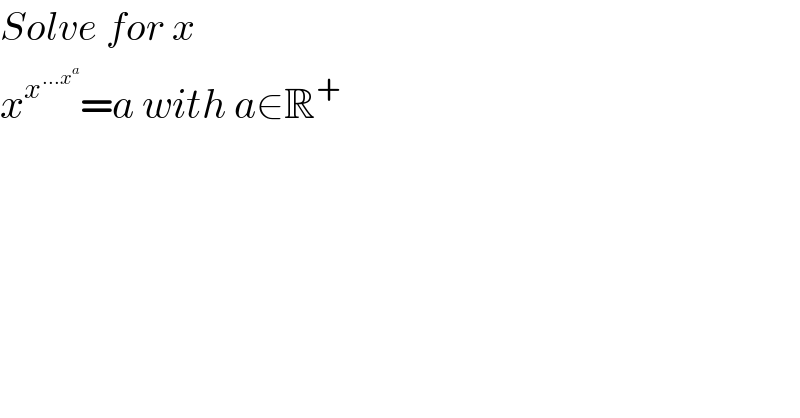
	Answered by Dwaipayan Shikari last updated on 03/Aug/20

	$X^{X . . . . X^{a}} = a$ $X^{X^{X^{X^{X . . . . . .}}}} = a$ $X^{a} = a$ ${(e^{- logx})}^{a} = \frac{1}{a}$ $- alogx e^{- alogx} = - logx$ $- alogx = W_{0} (- logx)$ $a = \frac{- W_{0} (- logx)}{logx}$
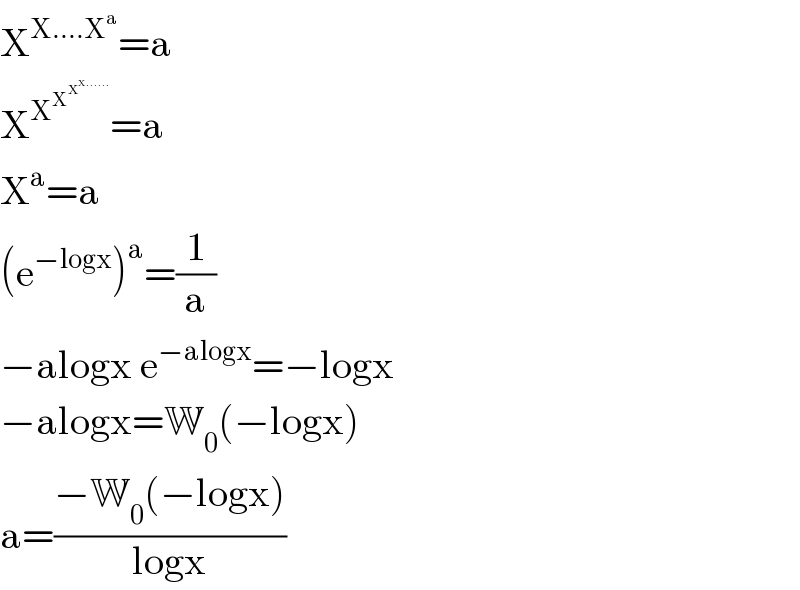
	Commented by mr W last updated on 03/Aug/20

	$w e s h o u l d s o l v e f o r x, n o t f o r a .$ $p l e a s e c o m p a r e f o l l o w i n g c a s e s :$ $x^{x^{\frac{1}{2}}} = \frac{1}{2}$ $x^{x^{x^{\frac{1}{2}}}} = \frac{1}{2}$
	Commented by Dwaipayan Shikari last updated on 03/Aug/20

	$X^{X^{X . . A}} = A$ $X^{X . . A} = A$ $X^{X^{X^{X^{X . . . . .}}}} = A$ $X^{A} = A$ $X = \sqrt[A]{A}$ $I t h i n k t h a t t w o f o l l o w i n g c a s e s a r e s a m e$
	Answered by mr W last updated on 03/Aug/20

	$w e s e e t h e r o o t o f x^{a} = a i s a l s o a r o o t$ $o f t h e o r i g i n a l e q u a t i o n .$ $f r o m x^{a} = a w e g e t x = a^{\frac{1}{a}}, i . e . t h e$ $o r i g i n a l e q u a t i o n h a s a t l e a s t a r o o t$ $x = a^{\frac{1}{a}} .$ $b u t d o e s t h e o r i g i n a l e q u a t i o n h a v e$ $m o r e t h a n t h i s r o o t ?$ $c a s e 1 : x^{x^{. . . x^{a}}} = a w i t h o d d n u m b e r o f$ $x i n t h e e q u a t i o n .$ $w e s e e t h e o r i g i n a l e q u a t i o n i s$ $e q u i v a l e n t t o x^{a} = a, t h a t m e a n s t h e$ $r o o t x = a^{\frac{1}{a}} i s t h e o n l y o n e r o o t o f$ $t h e o r i g i n a l e q u a t i o n .$ $c a s e 2 : x^{x^{. . . x^{a}}} = a w i t h e v e n n u m b e r o f$ $x i n t h e e q u a t i o n .$ $w e s e e t h e o r i g i n a l e q u a t i o n i s$ $e q u i v a l e n t t o x^{x^{a}} = a . w e c a n s o l v e i t$ $a s f o l l o w i n g :$ $x^{a} \ln x = \ln a$ $x^{a} \ln x^{a} = a \ln a$ $(\ln x^{a}) e^{(\ln x^{a})} = a \ln a$ $\Rightarrow \ln x^{a} = W (a \ln a)$ $\Rightarrow x = {[e^{W (a \ln a)}]}^{\frac{1}{a}} = {[\frac{a \ln a}{W (a \ln a)}]}^{\frac{1}{a}}$ $f o r a = 1 \Rightarrow w e s e e x = 1$ $f o r a > 1 \Rightarrow a \ln a > 0 \Rightarrow w e g e t o n e r o o t$ $f o r a < 1 \Rightarrow - \frac{1}{e} ⩽ a \ln a < 0 \Rightarrow w e g e t$ $t w o r o o t s (i f a \neq \frac{1}{e}) o r o n e r o o t (i f a = \frac{1}{e}) .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum