Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 106233 by malwaan last updated on 03/Aug/20

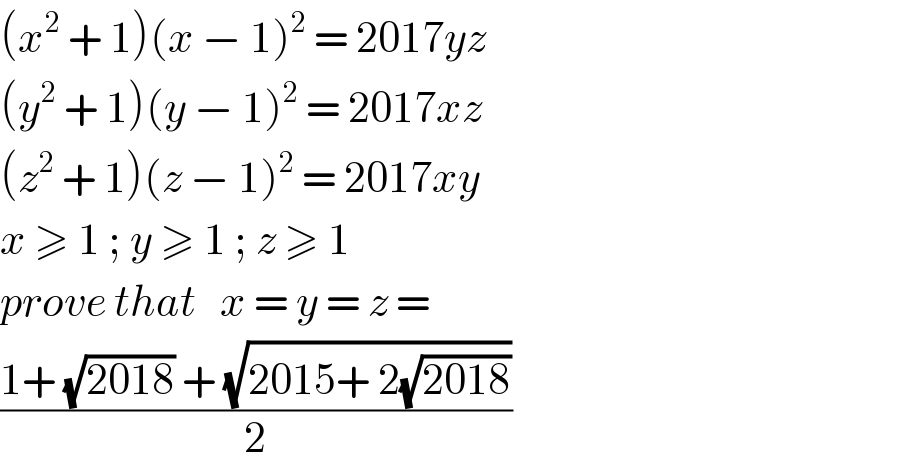
(x^2 + 1)(x − 1)^2 = 2017yz (y^2 + 1)(y − 1)^2 = 2017xz (z^2 + 1)(z − 1)^2 = 2017xy x ≥ 1 ; y ≥ 1 ; z ≥ 1 prove that x = y = z = ((1+ (√(2018)) + (√(2015+ 2(√(2018)))))/2)

$$\left({x}^{\mathrm{2}} \:+\:\mathrm{1}\right)\left({x}\:−\:\mathrm{1}\right)^{\mathrm{2}} \:=\:\mathrm{2017}{yz} \\ $$$$\left({y}^{\mathrm{2}} \:+\:\mathrm{1}\right)\left({y}\:−\:\mathrm{1}\right)^{\mathrm{2}} \:=\:\mathrm{2017}{xz} \\ $$$$\left({z}^{\mathrm{2}} \:+\:\mathrm{1}\right)\left({z}\:−\:\mathrm{1}\right)^{\mathrm{2}} \:=\:\mathrm{2017}{xy} \\ $$$${x}\:\geqslant\:\mathrm{1}\:;\:{y}\:\geqslant\:\mathrm{1}\:;\:{z}\:\geqslant\:\mathrm{1} \\ $$$${prove}\:{that}\:\:\:{x}\:=\:{y}\:=\:{z}\:= \\ $$$$\frac{\mathrm{1}+\:\sqrt{\mathrm{2018}}\:+\:\sqrt{\mathrm{2015}+\:\mathrm{2}\sqrt{\mathrm{2018}}}}{\mathrm{2}} \\ $$

Answered by Her_Majesty last updated on 04/Aug/20

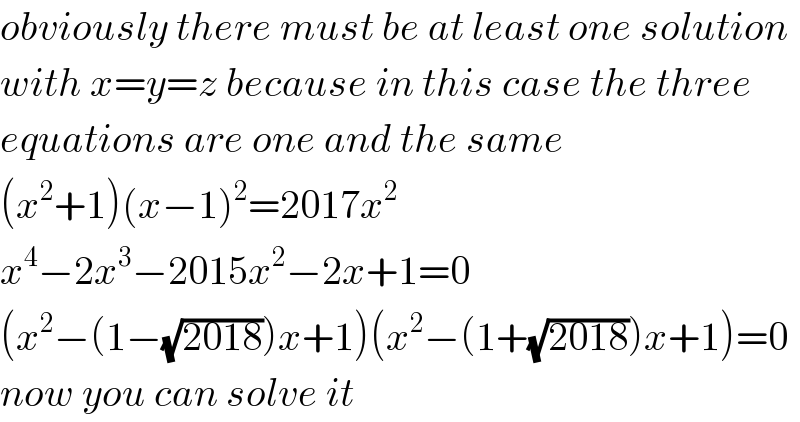
obviously there must be at least one solution with x=y=z because in this case the three equations are one and the same (x^2 +1)(x−1)^2 =2017x^2 x^4 −2x^3 −2015x^2 −2x+1=0 (x^2 −(1−(√(2018)))x+1)(x^2 −(1+(√(2018)))x+1)=0 now you can solve it

$${obviously}\:{there}\:{must}\:{be}\:{at}\:{least}\:{one}\:{solution} \\ $$$${with}\:{x}={y}={z}\:{because}\:{in}\:{this}\:{case}\:{the}\:{three} \\ $$$${equations}\:{are}\:{one}\:{and}\:{the}\:{same} \\ $$$$\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{2017}{x}^{\mathrm{2}} \\ $$$${x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{3}} −\mathrm{2015}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}=\mathrm{0} \\ $$$$\left({x}^{\mathrm{2}} −\left(\mathrm{1}−\sqrt{\mathrm{2018}}\right){x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −\left(\mathrm{1}+\sqrt{\mathrm{2018}}\right){x}+\mathrm{1}\right)=\mathrm{0} \\ $$$${now}\:{you}\:{can}\:{solve}\:{it} \\ $$

Commented by Sarah85 last updated on 04/Aug/20

you learn fast it seems

Commented by Her_Majesty last updated on 04/Aug/20

I forgot more than you′ll ever know...

$${I}\:{forgot}\:{more}\:{than}\:{you}'{ll}\:{ever}\:{know}... \\ $$

Commented by malwaan last updated on 04/Aug/20

thank you but how you factor the quartic equation which has 4 solutions only one is correct ?

$${thank}\:{you} \\ $$$${but}\:{how}\:{you}\:{factor}\:\:{the}\:{quartic}\: \\ $$$${equation}\:{which}\:{has}\:\mathrm{4}\:{solutions} \\ $$$${only}\:{one}\:{is}\:{correct}\:? \\ $$

Commented by Her_Majesty last updated on 04/Aug/20

(I) x^4 +ax^3 +bx^2 +cx+d=0 x=t−(a/4) leads to t^4 +pt^2 +qt+r=0 (t^2 −αt−β)(t^2 +αt−γ)=0 t^4 −(α^2 +β+γ)t^2 +(α−β)γt+βγ=0 { ((−(α^2 +β+γ)=p)),(((α−β)γ=q)),((βγ=r)) :} solving 2 of these for β and γ we get a 3^(rd) degree polynome for α^2 (α^2 )^3 +j(α^2 )^2 +k(α^2 )+l=0 if this has a useable solution we can find the square factors of (I)

$$\left({I}\right)\:{x}^{\mathrm{4}} +{ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{cx}+{d}=\mathrm{0} \\ $$$${x}={t}−\frac{{a}}{\mathrm{4}}\:{leads}\:{to} \\ $$$${t}^{\mathrm{4}} +{pt}^{\mathrm{2}} +{qt}+{r}=\mathrm{0} \\ $$$$\left({t}^{\mathrm{2}} −\alpha{t}−\beta\right)\left({t}^{\mathrm{2}} +\alpha{t}−\gamma\right)=\mathrm{0} \\ $$$${t}^{\mathrm{4}} −\left(\alpha^{\mathrm{2}} +\beta+\gamma\right){t}^{\mathrm{2}} +\left(\alpha−\beta\right)\gamma{t}+\beta\gamma=\mathrm{0} \\ $$$$\begin{cases}{−\left(\alpha^{\mathrm{2}} +\beta+\gamma\right)={p}}\\{\left(\alpha−\beta\right)\gamma={q}}\\{\beta\gamma={r}}\end{cases} \\ $$$${solving}\:\mathrm{2}\:{of}\:{these}\:{for}\:\beta\:{and}\:\gamma\:{we}\:{get}\:{a}\:\mathrm{3}^{{rd}} \:{degree} \\ $$$${polynome}\:{for}\:\alpha^{\mathrm{2}} \\ $$$$\left(\alpha^{\mathrm{2}} \right)^{\mathrm{3}} +{j}\left(\alpha^{\mathrm{2}} \right)^{\mathrm{2}} +{k}\left(\alpha^{\mathrm{2}} \right)+{l}=\mathrm{0} \\ $$$${if}\:{this}\:{has}\:{a}\:{useable}\:{solution}\:{we}\:{can}\:{find}\:{the} \\ $$$${square}\:{factors}\:{of}\:\left({I}\right) \\ $$

Commented by malwaan last updated on 05/Aug/20

I used another method long but easy

$${I}\:{used}\:{another}\:{method} \\ $$$${long}\:{but}\:{easy} \\ $$

Answered by malwaan last updated on 05/Aug/20

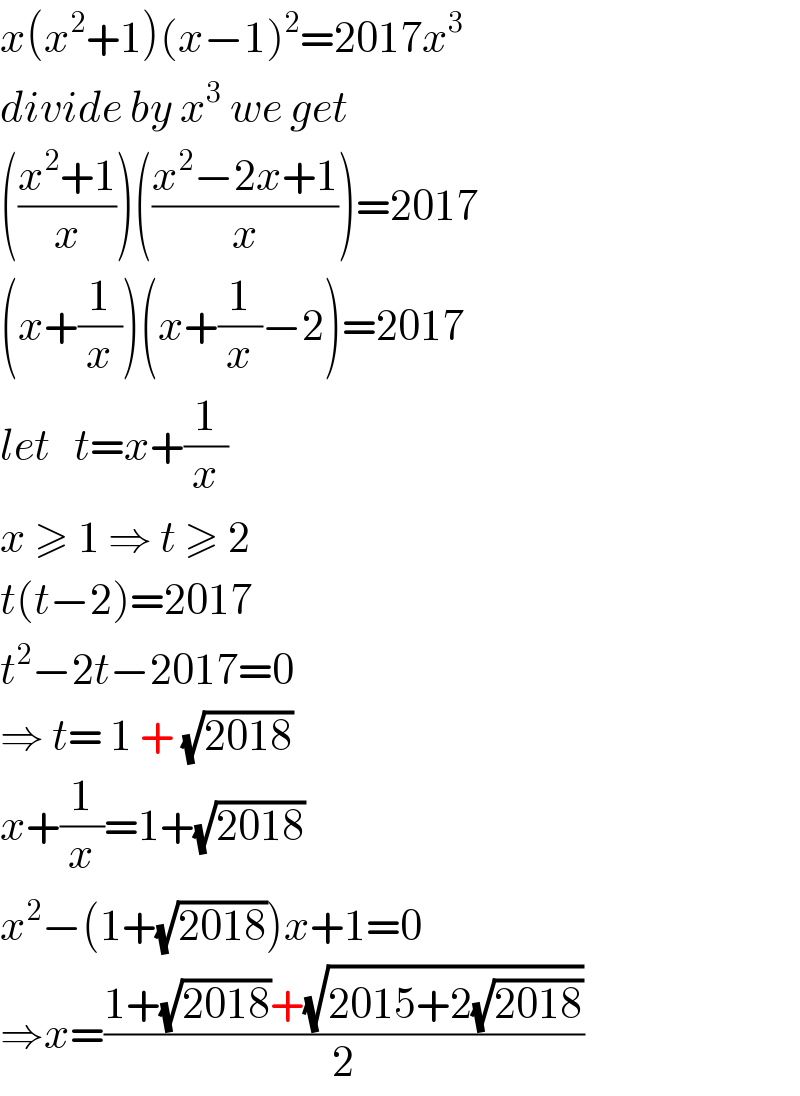
x(x^2 +1)(x−1)^2 =2017x^3 divide by x^3 we get (((x^2 +1)/x))(((x^2 −2x+1)/x))=2017 (x+(1/x))(x+(1/x)−2)=2017 let t=x+(1/x) x ≥ 1 ⇒ t ≥ 2 t(t−2)=2017 t^2 −2t−2017=0 ⇒ t= 1 + (√(2018)) x+(1/x)=1+(√(2018)) x^2 −(1+(√(2018)))x+1=0 ⇒x=((1+(√(2018))+(√(2015+2(√(2018)))))/2)

$${x}\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{2017}{x}^{\mathrm{3}} \\ $$$${divide}\:{by}\:{x}^{\mathrm{3}} \:{we}\:{get} \\ $$$$\left(\frac{{x}^{\mathrm{2}} +\mathrm{1}}{{x}}\right)\left(\frac{{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}}{{x}}\right)=\mathrm{2017} \\ $$$$\left({x}+\frac{\mathrm{1}}{{x}}\right)\left({x}+\frac{\mathrm{1}}{{x}}−\mathrm{2}\right)=\mathrm{2017} \\ $$$${let}\:\:\:{t}={x}+\frac{\mathrm{1}}{{x}} \\ $$$${x}\:\geqslant\:\mathrm{1}\:\Rightarrow\:{t}\:\geqslant\:\mathrm{2} \\ $$$${t}\left({t}−\mathrm{2}\right)=\mathrm{2017} \\ $$$${t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{2017}=\mathrm{0} \\ $$$$\Rightarrow\:{t}=\:\mathrm{1}\:+\:\sqrt{\mathrm{2018}} \\ $$$${x}+\frac{\mathrm{1}}{{x}}=\mathrm{1}+\sqrt{\mathrm{2018}} \\ $$$${x}^{\mathrm{2}} −\left(\mathrm{1}+\sqrt{\mathrm{2018}}\right){x}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{\mathrm{1}+\sqrt{\mathrm{2018}}+\sqrt{\mathrm{2015}+\mathrm{2}\sqrt{\mathrm{2018}}}}{\mathrm{2}} \\ $$

Commented by Her_Majesty last updated on 05/Aug/20

good!

$${good}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com