Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 106337 by Dwaipayan Shikari last updated on 04/Aug/20

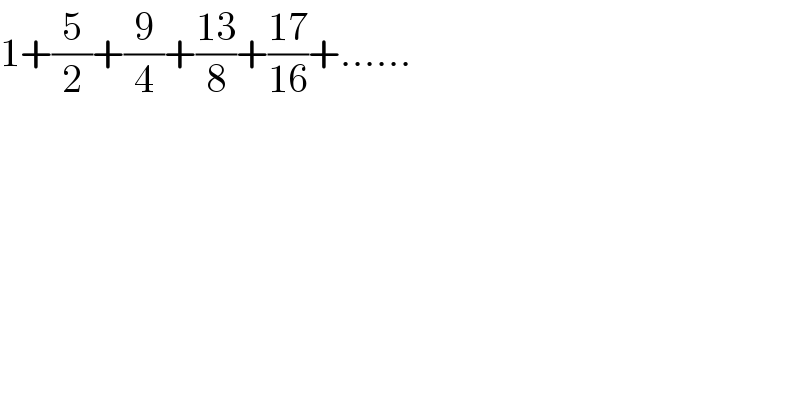
1+(5/2)+(9/4)+((13)/8)+((17)/(16))+......

$$\mathrm{1}+\frac{\mathrm{5}}{\mathrm{2}}+\frac{\mathrm{9}}{\mathrm{4}}+\frac{\mathrm{13}}{\mathrm{8}}+\frac{\mathrm{17}}{\mathrm{16}}+...... \\ $$

Commented by Dwaipayan Shikari last updated on 04/Aug/20

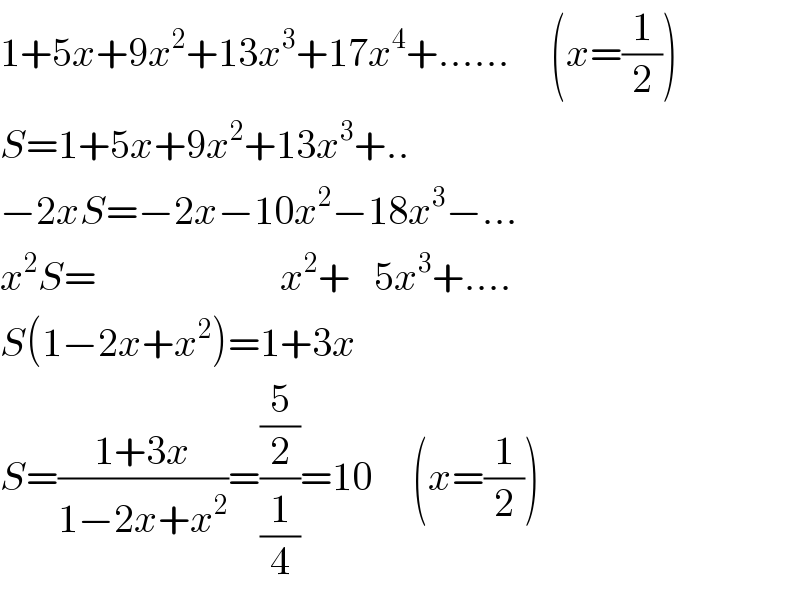
1+5x+9x^2 +13x^3 +17x^4 +...... (x=(1/2)) S=1+5x+9x^2 +13x^3 +.. −2xS=−2x−10x^2 −18x^3 −... x^2 S= x^2 + 5x^3 +.... S(1−2x+x^2 )=1+3x S=((1+3x)/(1−2x+x^2 ))=((5/2)/(1/4))=10 (x=(1/2))

$$\mathrm{1}+\mathrm{5}{x}+\mathrm{9}{x}^{\mathrm{2}} +\mathrm{13}{x}^{\mathrm{3}} +\mathrm{17}{x}^{\mathrm{4}} +......\:\:\:\:\:\left({x}=\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$${S}=\mathrm{1}+\mathrm{5}{x}+\mathrm{9}{x}^{\mathrm{2}} +\mathrm{13}{x}^{\mathrm{3}} +.. \\ $$$$−\mathrm{2}{xS}=−\mathrm{2}{x}−\mathrm{10}{x}^{\mathrm{2}} −\mathrm{18}{x}^{\mathrm{3}} −... \\ $$$${x}^{\mathrm{2}} {S}=\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} +\:\:\:\mathrm{5}{x}^{\mathrm{3}} +.... \\ $$$${S}\left(\mathrm{1}−\mathrm{2}{x}+{x}^{\mathrm{2}} \right)=\mathrm{1}+\mathrm{3}{x} \\ $$$${S}=\frac{\mathrm{1}+\mathrm{3}{x}}{\mathrm{1}−\mathrm{2}{x}+{x}^{\mathrm{2}} }=\frac{\frac{\mathrm{5}}{\mathrm{2}}}{\frac{\mathrm{1}}{\mathrm{4}}}=\mathrm{10}\:\:\:\:\:\left({x}=\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$

Commented by Ar Brandon last updated on 04/Aug/20

Amazing methode��

Commented by Dwaipayan Shikari last updated on 04/Aug/20

I have found this method idea on this book ���� https://drive.google.com/file/d/12J4x021yiK1X38OHkXoomTz_VuBlcIEt/view?usp=drivesdk

Commented by Ar Brandon last updated on 04/Aug/20

��Thanks bro

Answered by JDamian last updated on 04/Aug/20

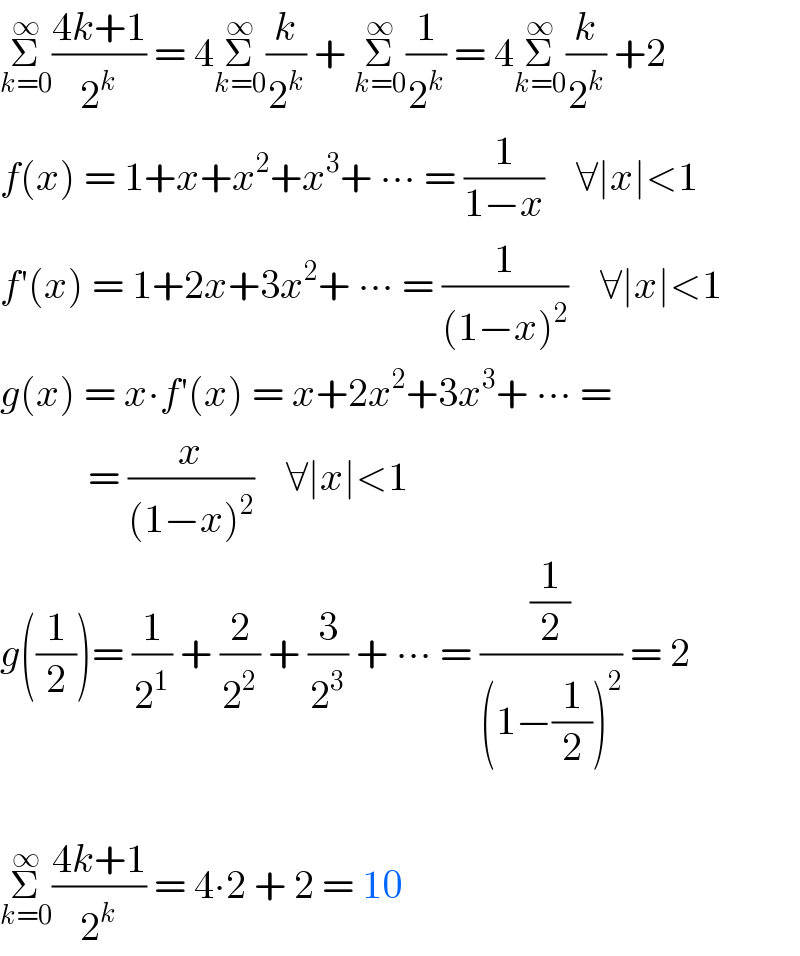
Σ_(k=0) ^∞ ((4k+1)/2^k ) = 4Σ_(k=0) ^∞ (k/2^k ) + Σ_(k=0) ^∞ (1/2^k ) = 4Σ_(k=0) ^∞ (k/2^k ) +2 f(x) = 1+x+x^2 +x^3 + ∙∙∙ = (1/(1−x)) ∀∣x∣<1 f′(x) = 1+2x+3x^2 + ∙∙∙ = (1/((1−x)^2 )) ∀∣x∣<1 g(x) = x∙f′(x) = x+2x^2 +3x^3 + ∙∙∙ = = (x/((1−x)^2 )) ∀∣x∣<1 g((1/2))= (1/2^1 ) + (2/2^2 ) + (3/2^3 ) + ∙∙∙ = ((1/2)/((1−(1/2))^2 )) = 2 Σ_(k=0) ^∞ ((4k+1)/2^k ) = 4∙2 + 2 = 10

$$\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{4}{k}+\mathrm{1}}{\mathrm{2}^{{k}} }\:=\:\mathrm{4}\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{k}}{\mathrm{2}^{{k}} }\:+\:\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{k}} }\:=\:\mathrm{4}\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{k}}{\mathrm{2}^{{k}} }\:+\mathrm{2} \\ $$$${f}\left({x}\right)\:=\:\mathrm{1}+{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +\:\centerdot\centerdot\centerdot\:=\:\frac{\mathrm{1}}{\mathrm{1}−{x}}\:\:\:\:\forall\mid{x}\mid<\mathrm{1} \\ $$$${f}'\left({x}\right)\:=\:\mathrm{1}+\mathrm{2}{x}+\mathrm{3}{x}^{\mathrm{2}} +\:\centerdot\centerdot\centerdot\:=\:\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }\:\:\:\:\forall\mid{x}\mid<\mathrm{1} \\ $$$${g}\left({x}\right)\:=\:{x}\centerdot{f}'\left({x}\right)\:=\:{x}+\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{x}^{\mathrm{3}} +\:\centerdot\centerdot\centerdot\:= \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\frac{{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }\:\:\:\:\forall\mid{x}\mid<\mathrm{1} \\ $$$${g}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{1}} }\:+\:\frac{\mathrm{2}}{\mathrm{2}^{\mathrm{2}} }\:+\:\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{3}} }\:+\:\centerdot\centerdot\centerdot\:=\:\frac{\frac{\mathrm{1}}{\mathrm{2}}}{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }\:=\:\mathrm{2} \\ $$$$ \\ $$$$\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{4}{k}+\mathrm{1}}{\mathrm{2}^{{k}} }\:=\:\mathrm{4}\centerdot\mathrm{2}\:+\:\mathrm{2}\:=\:\mathrm{10} \\ $$

Commented by JDamian last updated on 04/Aug/20

Sigma symbol looks small. How can I get a bigger sigma symbol?

Commented by Ar Brandon last updated on 04/Aug/20

By selecting the given symbol then touching the 3 small dots at the bottom-right corner. There you′ll find A^▼ and A^▲ . You can use them to increase or decrease the selected text.

$$\mathrm{By}\:\mathrm{selecting}\:\mathrm{the}\:\mathrm{given}\:\mathrm{symbol}\:\mathrm{then}\:\mathrm{touching}\:\mathrm{the}\:\mathrm{3}\:\mathrm{small} \\ $$$$\mathrm{dots}\:\mathrm{at}\:\mathrm{the}\:\mathrm{bottom}-\mathrm{right}\:\mathrm{corner}.\:\mathrm{There}\:\mathrm{you}'\mathrm{ll}\:\mathrm{find}\:\mathrm{A}^{\blacktrinagledown} \:\mathrm{and} \\ $$$$\mathrm{A}^{\blacktriangle} .\:\mathrm{You}\:\mathrm{can}\:\mathrm{use}\:\mathrm{them}\:\mathrm{to}\:\mathrm{increase}\:\mathrm{or}\:\mathrm{decrease}\:\mathrm{the}\: \\ $$$$\mathrm{selected}\:\mathrm{text}. \\ $$

Commented by JDamian last updated on 04/Aug/20

I edited several times the last line of my answer, I increased the size of the sigma symbol and saved... but my answer is unchanged -- it seems to work fine in the editor but the changes are not shown in my answer

Commented by Ar Brandon last updated on 04/Aug/20

You're right, Sir. I too faced the same problem while trying to demonstrate what I was talking about.

Commented by Tinku Tara last updated on 05/Aug/20

There is bigger sigma symbol press green color ★ key or press green ∫ sign and last∐ key. Several enhancement were made in last 2 weeks which are available in offline editor but not in forum as we giving user time to update to latest version: • Strike thru • underline • curly bracket below • font size for every character • table • borderless table (this is primarily intented for use in writing multiple line in drawing)

$$\mathrm{There}\:\mathrm{is}\:\mathrm{bigger}\:\mathrm{sigma}\:\mathrm{symbol} \\ $$$$\mathrm{press}\:\mathrm{green}\:\mathrm{color}\:\bigstar\:\mathrm{key}\:\mathrm{or} \\ $$$$\mathrm{press}\:\mathrm{green}\:\int\:\mathrm{sign}\:\mathrm{and} \\ $$$$\mathrm{last}\coprod\:\mathrm{key}.\: \\ $$$$\mathrm{Several}\:\mathrm{enhancement}\:\mathrm{were}\:\mathrm{made} \\ $$$$\mathrm{in}\:\mathrm{last}\:\mathrm{2}\:\mathrm{weeks}\:\mathrm{which}\:\mathrm{are}\:\mathrm{available} \\ $$$$\mathrm{in}\:\mathrm{offline}\:\mathrm{editor}\:\mathrm{but}\:\mathrm{not}\:\mathrm{in}\:\mathrm{forum} \\ $$$$\mathrm{as}\:\mathrm{we}\:\mathrm{giving}\:\mathrm{user}\:\mathrm{time}\:\mathrm{to}\:\mathrm{update} \\ $$$$\mathrm{to}\:\mathrm{latest}\:\mathrm{version}: \\ $$$$\bullet\:\mathrm{Strike}\:\mathrm{thru} \\ $$$$\bullet\:\mathrm{underline} \\ $$$$\bullet\:\mathrm{curly}\:\mathrm{bracket}\:\mathrm{below} \\ $$$$\bullet\:\mathrm{font}\:\mathrm{size}\:\mathrm{for}\:\mathrm{every}\:\mathrm{character} \\ $$$$\bullet\:\mathrm{table} \\ $$$$\bullet\:\mathrm{borderless}\:\mathrm{table}\:\left(\mathrm{this}\:\mathrm{is}\:\mathrm{primarily}\right. \\ $$$$\:\:\:\:\mathrm{intented}\:\mathrm{for}\:\mathrm{use}\:\mathrm{in}\:\mathrm{writing}\:\mathrm{multiple} \\ $$$$\left.\:\:\:\:\mathrm{line}\:\mathrm{in}\:\mathrm{drawing}\right) \\ $$

Commented by Tinku Tara last updated on 05/Aug/20

Commented by Tinku Tara last updated on 05/Aug/20

Commented by Tinku Tara last updated on 05/Aug/20

Answered by 1549442205PVT last updated on 04/Aug/20

The general term of the given sequence is ((4n−3)/2^(n−1) ).We need calculate Σ_(n=1) ^(∞) ((4n−3)/2^(n−1) )=4Σ_(n=1) ^(∞) (n/2^(n−1) )−3Σ_(n=1) ^(∞) (1/2^(n−1) ) Set S_k =Σ_(n=1) ^k (n/2^(n−1) )=(1/1)+(2/2)+(3/2^2 )+(4/2^3 )+...+(k/2^(k−1) ) (1/2)S_k =(1/2)+(2/2^2 )+(3/2^3 )+(4/2^4 )+....+((k−1)/2^(k−1) )+(k/2^k ) Substrating two above equalities we get 0.5S_k =1+(1/2)+(1/2^2 )+(1/2^3 )+...+(1/2^(k−1) )−(k/2^k ) =((1−((1/2))^(k+1) )/(1/2))−(k/2^k )⇒S_k =4(1−((1/2))^(k+1) )−(k/2^(k−1) ) ⇒Σ_(n=1) ^(∞) (n/2^(n−1) )=lim_(k→∞) S_k =lim_(k→∞) [4(1−((1/2))^(k+1) )−(k/2^(k−1) )]=4 Σ(1/2^(n−1) )=(1/1)+(1/2)+(1/2^2 )+...=lim_(n→∞) ((1/1)+(1/2)+(1/2^2 )+...+(1/2^n ))= lim_(n→∞) (((1−((1/2))^(n+1) ))/(1−(1/2)))=lim_(n→∞) [2(1−((1/2))^(n+1) )]=2 Hence, Σ_(n=1) ^(∞) ((4n−3)/2^(n−1) )=4Σ_(n=1) ^(∞) (n/2^(n−1) )−3Σ_(n=1) ^(∞) (1/2^(n−1) ) =4.4−3.2=10

$$\mathrm{The}\:\mathrm{general}\:\mathrm{term}\:\mathrm{of}\:\mathrm{the}\:\mathrm{given}\:\mathrm{sequence}\:\mathrm{is}\: \\ $$$$\frac{\mathrm{4n}−\mathrm{3}}{\mathrm{2}^{\mathrm{n}−\mathrm{1}} }.\mathrm{We}\:\mathrm{need}\:\mathrm{calculate}\:\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\Sigma}}\frac{\mathrm{4n}−\mathrm{3}}{\mathrm{2}^{\mathrm{n}−\mathrm{1}} }=\mathrm{4}\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\Sigma}}\frac{\mathrm{n}}{\mathrm{2}^{\mathrm{n}−\mathrm{1}} }−\mathrm{3}\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\Sigma}}\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}−\mathrm{1}} } \\ $$$$\mathrm{Set}\:\mathrm{S}_{\mathrm{k}} =\underset{\mathrm{n}=\mathrm{1}} {\overset{\mathrm{k}} {\sum}}\frac{\mathrm{n}}{\mathrm{2}^{\mathrm{n}−\mathrm{1}} }=\frac{\mathrm{1}}{\mathrm{1}}+\frac{\mathrm{2}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{4}}{\mathrm{2}^{\mathrm{3}} }+...+\frac{\mathrm{k}}{\mathrm{2}^{\mathrm{k}−\mathrm{1}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\mathrm{S}_{\mathrm{k}} =\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{2}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{3}} }+\frac{\mathrm{4}}{\mathrm{2}^{\mathrm{4}} }+....+\frac{\mathrm{k}−\mathrm{1}}{\mathrm{2}^{\mathrm{k}−\mathrm{1}} }+\frac{\mathrm{k}}{\mathrm{2}^{\mathrm{k}} } \\ $$$$\mathrm{Substrating}\:\mathrm{two}\:\mathrm{above}\:\mathrm{equalities}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{0}.\mathrm{5S}_{\mathrm{k}} =\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }+...+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{k}−\mathrm{1}} }−\frac{\mathrm{k}}{\mathrm{2}^{\mathrm{k}} } \\ $$$$=\frac{\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{k}+\mathrm{1}} }{\frac{\mathrm{1}}{\mathrm{2}}}−\frac{\mathrm{k}}{\mathrm{2}^{\mathrm{k}} }\Rightarrow\mathrm{S}_{\mathrm{k}} =\mathrm{4}\left(\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{k}+\mathrm{1}} \right)−\frac{\mathrm{k}}{\mathrm{2}^{\mathrm{k}−\mathrm{1}} } \\ $$$$\:\Rightarrow\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\Sigma}}\frac{\mathrm{n}}{\mathrm{2}^{\mathrm{n}−\mathrm{1}} }=\underset{\mathrm{k}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{S}_{\mathrm{k}} =\underset{\mathrm{k}\rightarrow\infty} {\mathrm{lim}}\left[\mathrm{4}\left(\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{k}+\mathrm{1}} \right)−\frac{\mathrm{k}}{\mathrm{2}^{\mathrm{k}−\mathrm{1}} }\right]=\mathrm{4} \\ $$$$\Sigma\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}−\mathrm{1}} }=\frac{\mathrm{1}}{\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+...=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{1}}{\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+...+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\right)= \\ $$$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\frac{\left(\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{n}+\mathrm{1}} \right)}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}}=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left[\mathrm{2}\left(\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{n}+\mathrm{1}} \right)\right]=\mathrm{2} \\ $$$$\mathrm{Hence},\:\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\Sigma}}\frac{\mathrm{4n}−\mathrm{3}}{\mathrm{2}^{\mathrm{n}−\mathrm{1}} }=\mathrm{4}\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\Sigma}}\frac{\mathrm{n}}{\mathrm{2}^{\mathrm{n}−\mathrm{1}} }−\mathrm{3}\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\Sigma}}\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}−\mathrm{1}} } \\ $$$$=\mathrm{4}.\mathrm{4}−\mathrm{3}.\mathrm{2}=\mathrm{10} \\ $$

Commented by Dwaipayan Shikari last updated on 04/Aug/20

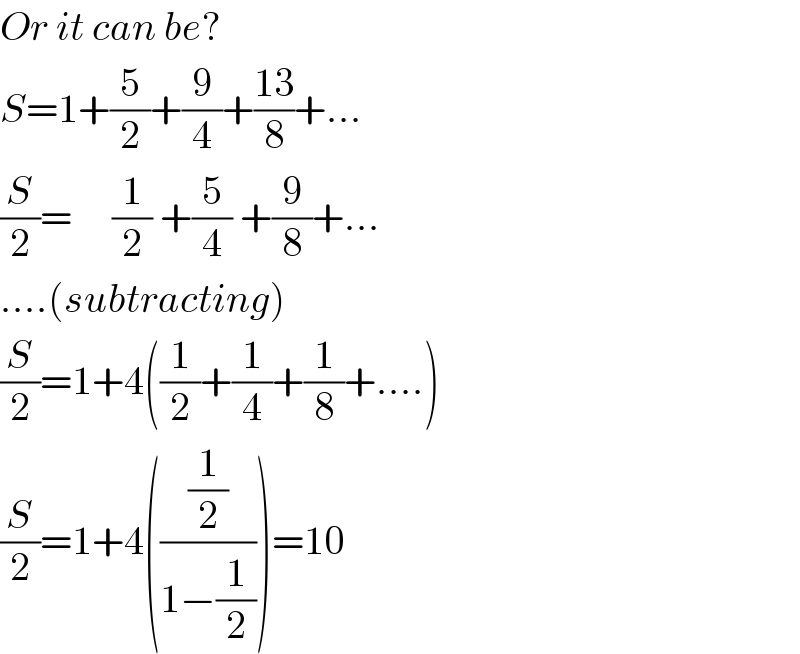
Or it can be? S=1+(5/2)+(9/4)+((13)/8)+... (S/2)= (1/2) +(5/4) +(9/8)+... ....(subtracting) (S/2)=1+4((1/2)+(1/4)+(1/8)+....) (S/2)=1+4(((1/2)/(1−(1/2))))=10

$${Or}\:{it}\:{can}\:{be}? \\ $$$${S}=\mathrm{1}+\frac{\mathrm{5}}{\mathrm{2}}+\frac{\mathrm{9}}{\mathrm{4}}+\frac{\mathrm{13}}{\mathrm{8}}+... \\ $$$$\frac{{S}}{\mathrm{2}}=\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{5}}{\mathrm{4}}\:+\frac{\mathrm{9}}{\mathrm{8}}+... \\ $$$$....\left({subtracting}\right) \\ $$$$\frac{{S}}{\mathrm{2}}=\mathrm{1}+\mathrm{4}\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{8}}+....\right) \\ $$$$\frac{{S}}{\mathrm{2}}=\mathrm{1}+\mathrm{4}\left(\frac{\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}}\right)=\mathrm{10} \\ $$

Answered by mathmax by abdo last updated on 04/Aug/20

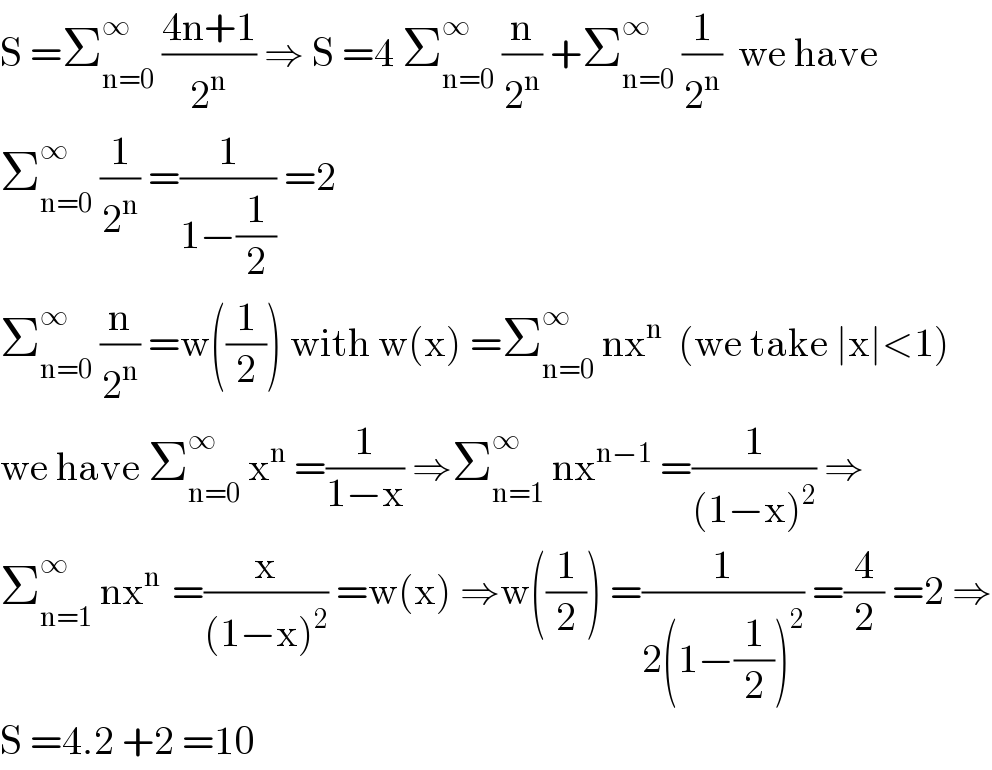
S =Σ_(n=0) ^∞ ((4n+1)/2^n ) ⇒ S =4 Σ_(n=0) ^∞ (n/2^n ) +Σ_(n=0) ^∞ (1/2^n ) we have Σ_(n=0) ^∞ (1/2^n ) =(1/(1−(1/2))) =2 Σ_(n=0) ^∞ (n/2^n ) =w((1/2)) with w(x) =Σ_(n=0) ^∞ nx^n (we take ∣x∣<1) we have Σ_(n=0) ^∞ x^n =(1/(1−x)) ⇒Σ_(n=1) ^∞ nx^(n−1) =(1/((1−x)^2 )) ⇒ Σ_(n=1) ^∞ nx^(n ) =(x/((1−x)^2 )) =w(x) ⇒w((1/2)) =(1/(2(1−(1/2))^2 )) =(4/2) =2 ⇒ S =4.2 +2 =10

$$\mathrm{S}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{4n}+\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\:\Rightarrow\:\mathrm{S}\:=\mathrm{4}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{n}}{\mathrm{2}^{\mathrm{n}} }\:+\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\:=\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}}\:=\mathrm{2}\:\: \\ $$$$\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{n}}{\mathrm{2}^{\mathrm{n}} }\:=\mathrm{w}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:\mathrm{with}\:\mathrm{w}\left(\mathrm{x}\right)\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{nx}^{\mathrm{n}} \:\:\left(\mathrm{we}\:\mathrm{take}\:\mid\mathrm{x}\mid<\mathrm{1}\right) \\ $$$$\mathrm{we}\:\mathrm{have}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{x}^{\mathrm{n}} \:=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}\:\Rightarrow\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{nx}^{\mathrm{n}−\mathrm{1}} \:=\frac{\mathrm{1}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{nx}^{\mathrm{n}\:} \:=\frac{\mathrm{x}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} }\:=\mathrm{w}\left(\mathrm{x}\right)\:\Rightarrow\mathrm{w}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }\:=\frac{\mathrm{4}}{\mathrm{2}}\:=\mathrm{2}\:\Rightarrow \\ $$$$\mathrm{S}\:=\mathrm{4}.\mathrm{2}\:+\mathrm{2}\:=\mathrm{10} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com