Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 106444 by mathdave last updated on 05/Aug/20

Answered by nimnim last updated on 05/Aug/20

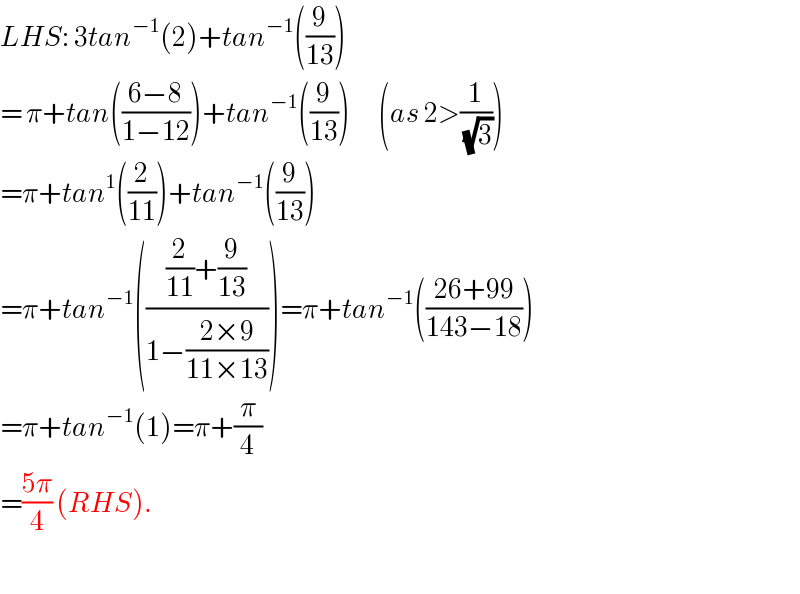
LHS: 3tan^(−1) (2)+tan^(−1) ((9/(13))) = π+tan(((6−8)/(1−12)))+tan^(−1) ((9/(13))) (as 2>(1/(√3))) =π+tan^1 ((2/(11)))+tan^(−1) ((9/(13))) =π+tan^(−1) ((((2/(11))+(9/(13)))/(1−((2×9)/(11×13)))))=π+tan^(−1) (((26+99)/(143−18))) =π+tan^(−1) (1)=π+(π/4) =((5π)/4) (RHS).

$${LHS}:\:\mathrm{3}{tan}^{−\mathrm{1}} \left(\mathrm{2}\right)+{tan}^{−\mathrm{1}} \left(\frac{\mathrm{9}}{\mathrm{13}}\right) \\ $$$$=\:\pi+{tan}\left(\frac{\mathrm{6}−\mathrm{8}}{\mathrm{1}−\mathrm{12}}\right)+{tan}^{−\mathrm{1}} \left(\frac{\mathrm{9}}{\mathrm{13}}\right)\:\:\:\:\:\:\:\left({as}\:\mathrm{2}>\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\right) \\ $$$$=\pi+{tan}^{\mathrm{1}} \left(\frac{\mathrm{2}}{\mathrm{11}}\right)+{tan}^{−\mathrm{1}} \left(\frac{\mathrm{9}}{\mathrm{13}}\right) \\ $$$$=\pi+{tan}^{−\mathrm{1}} \left(\frac{\frac{\mathrm{2}}{\mathrm{11}}+\frac{\mathrm{9}}{\mathrm{13}}}{\mathrm{1}−\frac{\mathrm{2}×\mathrm{9}}{\mathrm{11}×\mathrm{13}}}\right)=\pi+{tan}^{−\mathrm{1}} \left(\frac{\mathrm{26}+\mathrm{99}}{\mathrm{143}−\mathrm{18}}\right) \\ $$$$=\pi+{tan}^{−\mathrm{1}} \left(\mathrm{1}\right)=\pi+\frac{\pi}{\mathrm{4}} \\ $$$$=\frac{\mathrm{5}\pi}{\mathrm{4}}\:\left({RHS}\right). \\ $$$$ \\ $$

Commented by mathdave last updated on 05/Aug/20

thank

$${thank} \\ $$

Commented by mathdave last updated on 05/Aug/20

hasfor me i set β=3tan^(−1) (2) then 2=tan^(−1) ((3/β)) how did u get 3tan^(−1) (2)=π+tan^(−1) (((6−8)/(1−12))) is there any formular or rule that guide this pls i need ur explanation

$${hasfor}\:{me}\:{i}\:{set}\:\beta=\mathrm{3tan}^{−\mathrm{1}} \left(\mathrm{2}\right)\:\:\:{then}\:\:\mathrm{2}=\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{3}}{\beta}\right) \\ $$$${how}\:{did}\:{u}\:{get}\:\:\mathrm{3tan}^{−\mathrm{1}} \left(\mathrm{2}\right)=\pi+\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{6}−\mathrm{8}}{\mathrm{1}−\mathrm{12}}\right) \\ $$$${is}\:{there}\:{any}\:{formular}\:{or}\:{rule}\:{that}\:{guide}\:{this} \\ $$$${pls}\:{i}\:{need}\:{ur}\:{explanation} \\ $$

Commented by mathdave last updated on 05/Aug/20

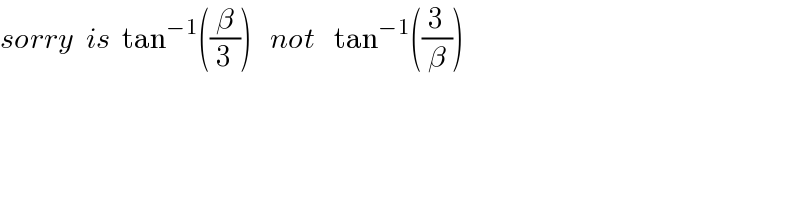
sorry is tan^(−1) ((β/3)) not tan^(−1) ((3/β))

$${sorry}\:\:{is}\:\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\beta}{\mathrm{3}}\right)\:\:\:{not}\:\:\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{3}}{\beta}\right) \\ $$

Commented by nimnim last updated on 05/Aug/20

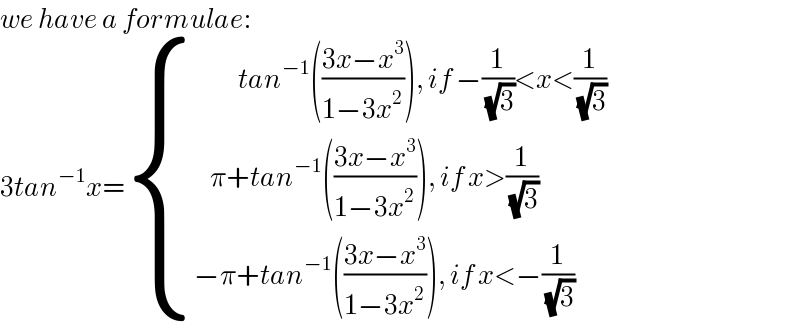
we have a formulae: 3tan^(−1) x= { (( tan^(−1) (((3x−x^3 )/(1−3x^2 ))), if −(1/(√3))<x<(1/(√3)))),(( π+tan^(−1) (((3x−x^3 )/(1−3x^2 ))), if x>(1/(√3)))),((−π+tan^(−1) (((3x−x^3 )/(1−3x^2 ))), if x<−(1/(√3)))) :}

$${we}\:{have}\:{a}\:{formulae}: \\ $$$$\mathrm{3}{tan}^{−\mathrm{1}} {x}=\begin{cases}{\:\:\:\:\:\:\:\:\:\:\:{tan}^{−\mathrm{1}} \left(\frac{\mathrm{3}{x}−{x}^{\mathrm{3}} }{\mathrm{1}−\mathrm{3}{x}^{\mathrm{2}} }\right),\:{if}\:−\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}<{x}<\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}}\\{\:\:\:\:\pi+{tan}^{−\mathrm{1}} \left(\frac{\mathrm{3}{x}−{x}^{\mathrm{3}} }{\mathrm{1}−\mathrm{3}{x}^{\mathrm{2}} }\right),\:{if}\:{x}>\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}}\\{−\pi+{tan}^{−\mathrm{1}} \left(\frac{\mathrm{3}{x}−{x}^{\mathrm{3}} }{\mathrm{1}−\mathrm{3}{x}^{\mathrm{2}} }\right),\:{if}\:{x}<−\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}}\end{cases} \\ $$

Commented by mathdave last updated on 05/Aug/20

thank so much but wait oo incase if we re now given 5tan^(−1) (3) hw can we set formular for ds .i really wanna kwn more fact on ds

$${thank}\:{so}\:{much}\:{but}\:\:{wait}\:\:{oo}\:{incase}\:{if}\:{we}\:{re} \\ $$$${now}\:{given}\:\:\mathrm{5tan}^{−\mathrm{1}} \left(\mathrm{3}\right)\:{hw}\:{can}\:{we}\:{set}\:{formular}\:{for} \\ $$$${ds}\:.{i}\:{really}\:{wanna}\:{kwn}\:{more}\:{fact}\:{on}\:{ds} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com