
Question and Answers Forum
Question Number 106479 by mohammad17 last updated on 05/Aug/20

Answered by Rio Michael last updated on 05/Aug/20
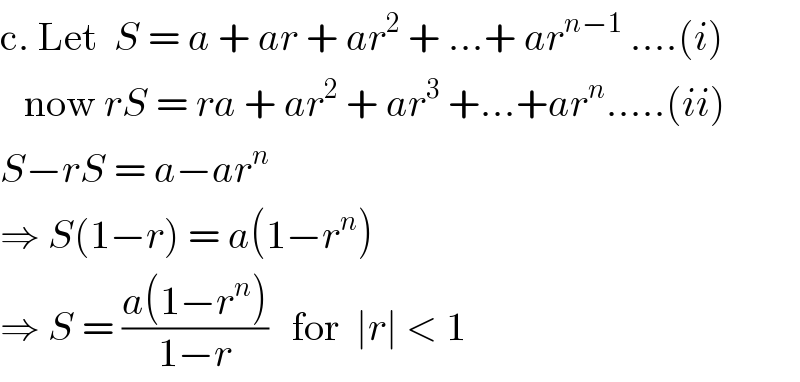
Answered by Rio Michael last updated on 05/Aug/20
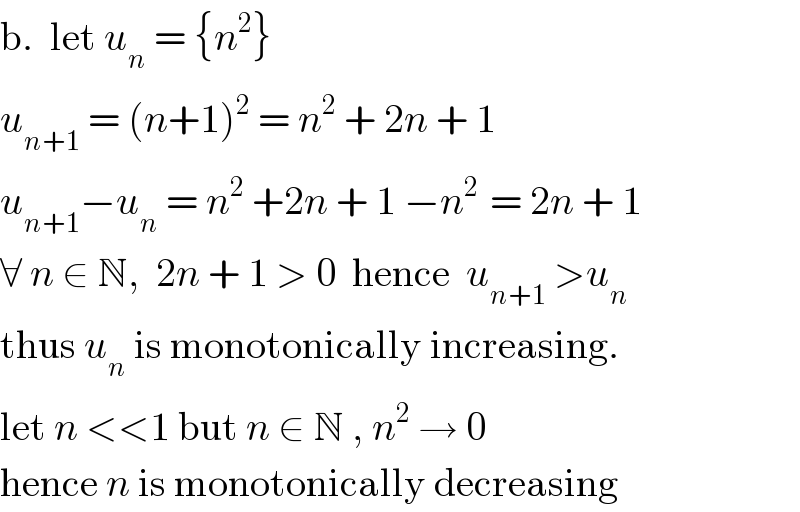
Answered by Rio Michael last updated on 05/Aug/20
![a. let u_n = {(1 + (5/n))^n }_(n=1) ^∞ If lim_(n→∞) u_n = L , L ∈ R ⇒ u_n converges otherwise it is divergent. lim_(n→∞) (1 + (5/n))^n = e^5 you need proof? here is it let (5/n) = (1/m) as n →∞, m → ∞ ⇒ 5m = n lim_(n→∞) (1 + (5/n))^n = lim_(m→∞) [(1 + (1/m))^m ]^5 = e^5 ⇒ u_n is convergnt](Q106502.png)
| ||
Question and Answers Forum | ||
Question Number 106479 by mohammad17 last updated on 05/Aug/20 | ||
 | ||
Answered by Rio Michael last updated on 05/Aug/20 | ||
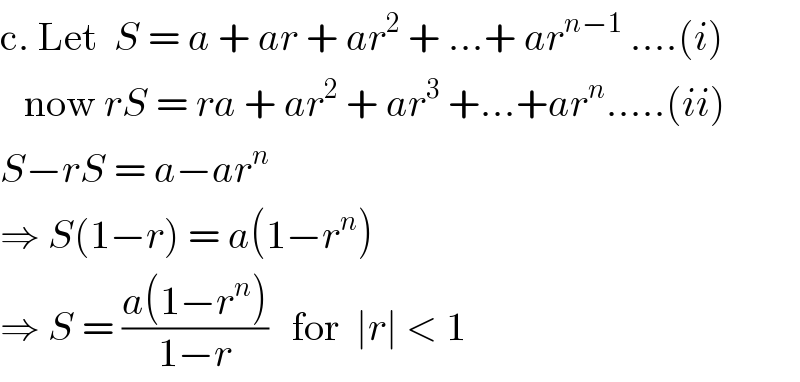 | ||
| ||
Answered by Rio Michael last updated on 05/Aug/20 | ||
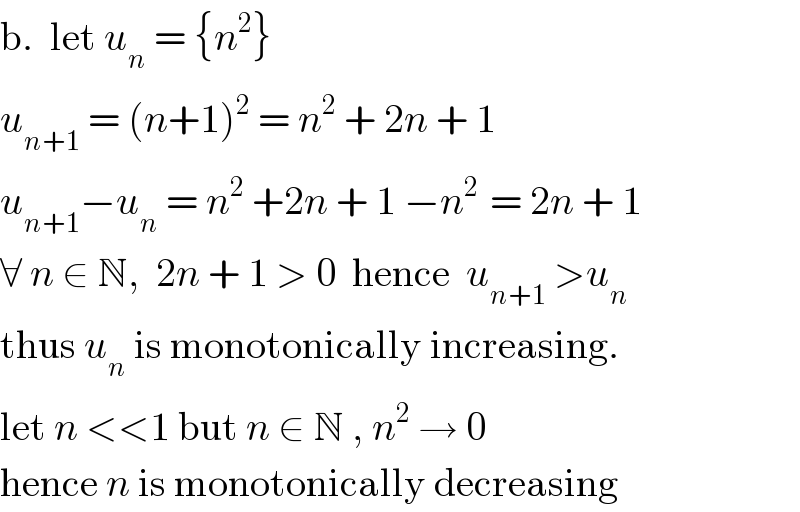 | ||
| ||
Answered by Rio Michael last updated on 05/Aug/20 | ||
![a. let u_n = {(1 + (5/n))^n }_(n=1) ^∞ If lim_(n→∞) u_n = L , L ∈ R ⇒ u_n converges otherwise it is divergent. lim_(n→∞) (1 + (5/n))^n = e^5 you need proof? here is it let (5/n) = (1/m) as n →∞, m → ∞ ⇒ 5m = n lim_(n→∞) (1 + (5/n))^n = lim_(m→∞) [(1 + (1/m))^m ]^5 = e^5 ⇒ u_n is convergnt](Q106502.png) | ||
| ||