Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 106505 by Ar Brandon last updated on 05/Aug/20

Show thatlim_(n→∞) [((n!)/((n−x)!n^x ))]=1

$$\mathrm{Show}\:\mathrm{that}\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left[\frac{\mathrm{n}!}{\left(\mathrm{n}−\mathrm{x}\right)!\mathrm{n}^{\mathrm{x}} }\right]=\mathrm{1} \\ $$

Answered by Dwaipayan Shikari last updated on 05/Aug/20

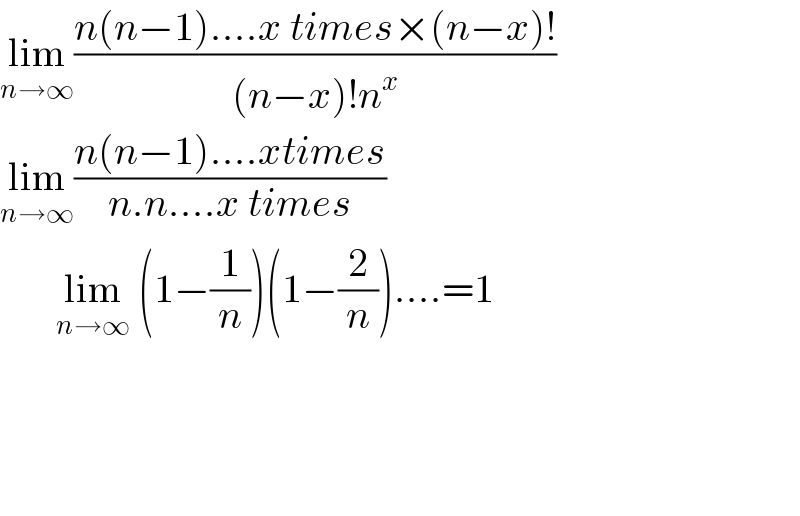
lim_(n→∞) ((n(n−1)....x times×(n−x)!)/((n−x)!n^x )) lim_(n→∞) ((n(n−1)....xtimes)/(n.n....x times)) lim_(n→∞) (1−(1/n))(1−(2/n))....=1

$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{n}\left({n}−\mathrm{1}\right)....{x}\:{times}×\left({n}−{x}\right)!}{\left({n}−{x}\right)!{n}^{{x}} } \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{n}\left({n}−\mathrm{1}\right)....{xtimes}}{{n}.{n}....{x}\:{times}} \\ $$$$\:\:\:\:\:\:\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left(\mathrm{1}−\frac{\mathrm{1}}{{n}}\right)\left(\mathrm{1}−\frac{\mathrm{2}}{{n}}\right)....=\mathrm{1} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by Ar Brandon last updated on 05/Aug/20

��Thanks. �� I arrived there while trying to demonstrate that as n and p go to infinity and zero respectively, the binomial probability distribution becomes approximately equal to the poisson distribution.

Commented by Dwaipayan Shikari last updated on 05/Aug/20

������

Commented by Dwaipayan Shikari last updated on 05/Aug/20

Are you from France?

Commented by Dwaipayan Shikari last updated on 05/Aug/20

Là nuit Bonne nuit

Commented by mathmax by abdo last updated on 06/Aug/20

here x is real not integr ...!

$$\mathrm{here}\:\mathrm{x}\:\mathrm{is}\:\mathrm{real}\:\mathrm{not}\:\mathrm{integr}\:...! \\ $$

Commented by Ar Brandon last updated on 06/Aug/20

����Bonne Nuit, mon ami Shikari.��

Answered by mathmax by abdo last updated on 06/Aug/20

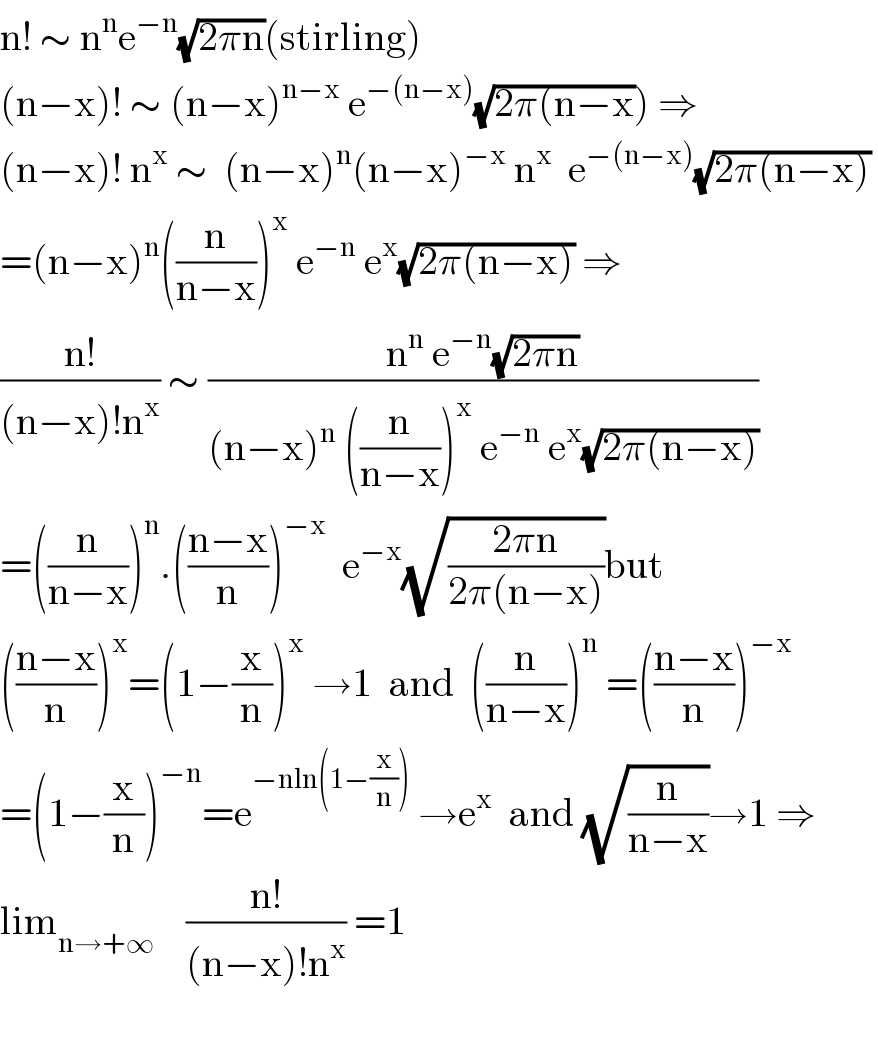
n! ∼ n^n e^(−n) (√(2πn))(stirling) (n−x)! ∼ (n−x)^(n−x) e^(−(n−x)) (√(2π(n−x))) ⇒ (n−x)! n^x ∼ (n−x)^n (n−x)^(−x) n^x e^(−(n−x)) (√(2π(n−x))) =(n−x)^n ((n/(n−x)))^x e^(−n) e^x (√(2π(n−x))) ⇒ ((n!)/((n−x)!n^x )) ∼ ((n^n e^(−n) (√(2πn)))/((n−x)^n ((n/(n−x)))^x e^(−n) e^x (√(2π(n−x))))) =((n/(n−x)))^n .(((n−x)/n))^(−x) e^(−x) (√((2πn)/(2π(n−x))))but (((n−x)/n))^x =(1−(x/n))^x →1 and ((n/(n−x)))^n =(((n−x)/n))^(−x) =(1−(x/n))^(−n) =e^(−nln(1−(x/n))) →e^x and (√(n/(n−x)))→1 ⇒ lim_(n→+∞) ((n!)/((n−x)!n^x )) =1

$$\mathrm{n}!\:\sim\:\mathrm{n}^{\mathrm{n}} \mathrm{e}^{−\mathrm{n}} \sqrt{\mathrm{2}\pi\mathrm{n}}\left(\mathrm{stirling}\right) \\ $$$$\left.\left(\mathrm{n}−\mathrm{x}\right)!\:\sim\:\left(\mathrm{n}−\mathrm{x}\right)^{\mathrm{n}−\mathrm{x}} \:\mathrm{e}^{−\left(\mathrm{n}−\mathrm{x}\right)} \sqrt{\mathrm{2}\pi\left(\mathrm{n}−\mathrm{x}\right.}\right)\:\Rightarrow \\ $$$$\left(\mathrm{n}−\mathrm{x}\right)!\:\mathrm{n}^{\mathrm{x}} \:\sim\:\:\left(\mathrm{n}−\mathrm{x}\right)^{\mathrm{n}} \left(\mathrm{n}−\mathrm{x}\right)^{−\mathrm{x}} \:\mathrm{n}^{\mathrm{x}} \:\:\mathrm{e}^{−\left(\mathrm{n}−\mathrm{x}\right)} \sqrt{\mathrm{2}\pi\left(\mathrm{n}−\mathrm{x}\right)}\: \\ $$$$=\left(\mathrm{n}−\mathrm{x}\right)^{\mathrm{n}} \left(\frac{\mathrm{n}}{\mathrm{n}−\mathrm{x}}\right)^{\mathrm{x}} \:\mathrm{e}^{−\mathrm{n}} \:\mathrm{e}^{\mathrm{x}} \sqrt{\mathrm{2}\pi\left(\mathrm{n}−\mathrm{x}\right)}\:\Rightarrow \\ $$$$\frac{\mathrm{n}!}{\left(\mathrm{n}−\mathrm{x}\right)!\mathrm{n}^{\mathrm{x}} }\:\sim\:\frac{\mathrm{n}^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{n}} \sqrt{\mathrm{2}\pi\mathrm{n}}}{\left(\mathrm{n}−\mathrm{x}\right)^{\mathrm{n}} \:\left(\frac{\mathrm{n}}{\mathrm{n}−\mathrm{x}}\right)^{\mathrm{x}} \:\mathrm{e}^{−\mathrm{n}} \:\mathrm{e}^{\mathrm{x}} \sqrt{\mathrm{2}\pi\left(\mathrm{n}−\mathrm{x}\right)}} \\ $$$$=\left(\frac{\mathrm{n}}{\mathrm{n}−\mathrm{x}}\right)^{\mathrm{n}} .\left(\frac{\mathrm{n}−\mathrm{x}}{\mathrm{n}}\right)^{−\mathrm{x}} \:\:\mathrm{e}^{−\mathrm{x}} \sqrt{\frac{\mathrm{2}\pi\mathrm{n}}{\mathrm{2}\pi\left(\mathrm{n}−\mathrm{x}\right)}}\mathrm{but} \\ $$$$\left(\frac{\mathrm{n}−\mathrm{x}}{\mathrm{n}}\right)^{\mathrm{x}} =\left(\mathrm{1}−\frac{\mathrm{x}}{\mathrm{n}}\right)^{\mathrm{x}} \:\rightarrow\mathrm{1}\:\:\mathrm{and}\:\:\left(\frac{\mathrm{n}}{\mathrm{n}−\mathrm{x}}\right)^{\mathrm{n}} \:=\left(\frac{\mathrm{n}−\mathrm{x}}{\mathrm{n}}\right)^{−\mathrm{x}} \\ $$$$=\left(\mathrm{1}−\frac{\mathrm{x}}{\mathrm{n}}\right)^{−\mathrm{n}} =\mathrm{e}^{−\mathrm{nln}\left(\mathrm{1}−\frac{\mathrm{x}}{\mathrm{n}}\right)} \:\rightarrow\mathrm{e}^{\mathrm{x}} \:\:\mathrm{and}\:\sqrt{\frac{\mathrm{n}}{\mathrm{n}−\mathrm{x}}}\rightarrow\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\:\:\:\frac{\mathrm{n}!}{\left(\mathrm{n}−\mathrm{x}\right)!\mathrm{n}^{\mathrm{x}} }\:=\mathrm{1} \\ $$$$\:\:\:\:\:\: \\ $$

Commented by Ar Brandon last updated on 06/Aug/20

Thanks Sir. Sorry I didn't precise that. In my case x is a natural number. But still arrived at thesame result. Thanks��

Commented by Dwaipayan Shikari last updated on 06/Aug/20

Thanking you for your corrections

Terms of Service

Privacy Policy

Contact: info@tinkutara.com