Question Number 106555 by M±th+et+s last updated on 06/Aug/20
$$\int_{\mathrm{0}} ^{\mathrm{4}} \int_{\sqrt{{y}}} ^{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{3}} }{dx}\:{dy} \\ $$
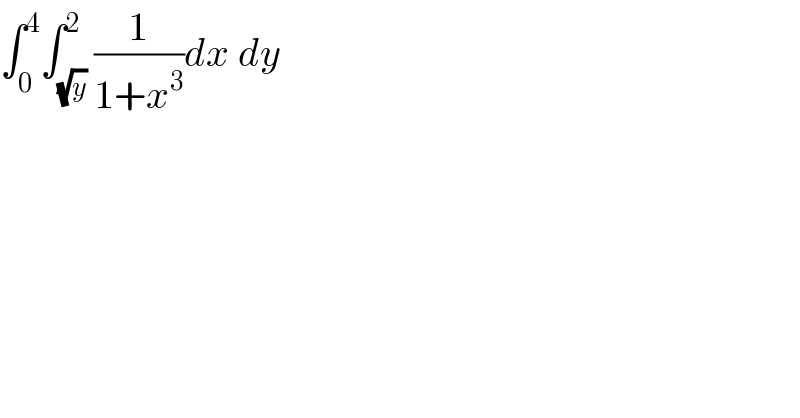
Commented by bobhans last updated on 06/Aug/20
$$=\mathrm{syntax}\:\mathrm{error}= \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{4}} {\int}}\underset{\sqrt{\mathrm{y}}} {\overset{\mathrm{2}} {\int}}\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\mathrm{3}} }\:\mathrm{dydx}\: \\ $$
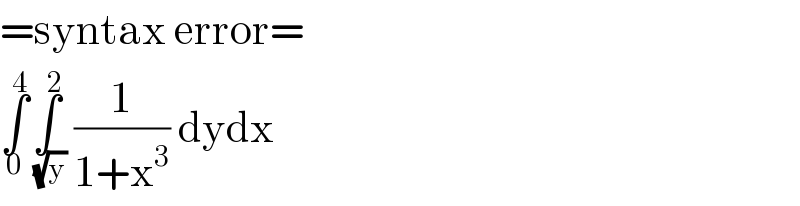
Answered by mathmax by abdo last updated on 06/Aug/20
![I =∫_0 ^4 (∫_(√y) ^2 (dx/(1+x^3 )))dy =∫_0 ^4 A(y)dy with A(y) =∫_(√y) ^(2 ) (dx/(x^3 +1)) let decompose f(x) =(1/(x^3 +1)) =(1/((x+1)(x^2 −x+1))) f(x) =(a/(x+1)) +((bx +c)/(x^2 −x+1)) we get a=(1/3) lim_(x→+∞) xf(x) =0 =a+b ⇒b =−(1/3) ⇒f(x)=(1/(3(x+1)))+((−(1/3)x+c)/(x^2 −x+1)) f(0) =1 =(1/3) +c ⇒c =(2/3) ⇒f(x) =(1/(3(x+1)))+((−(1/3)x+(2/3))/(x^2 −x+1)) ⇒∫ f(x) dx =(1/3)ln∣x+1∣−(1/3)∫ ((x−2)/(x^2 −x+1))dx but ∫ ((x−2)/(x^2 −x+1))dx =(1/2)∫ ((2x−1−3)/(x^2 −x+1))dx =(1/2)ln(x^2 −x+1)−(3/2)∫ (dx/(x^2 −x+1)) ∫ (dx/(x^2 −x+1))dx =∫ (dx/(x^2 −2(1/2)x +(1/4)+(3/4))) =∫ (dx/((x−(1/2))^2 +(3/4))) =_(x−(1/2)=((√3)/2)u) (4/3) ∫ (1/(u^2 +1)).((√3)/2)du =(2/(√3)) arctan(((2x−1)/(√3))) +c ⇒ ∫ ((x−2)/(x^2 −x+1))dx =(1/2)ln(x^2 −x+1)−(√3)arctan(((2x−1)/(√3))) ⇒ ∫ f(x)dx =(1/3)ln∣x+1∣−(1/6)ln(x^2 −x+1)+((√3)/3) arctan(((2x−1)/(√3))) ⇒ A(y) =[(1/3)ln∣x+1∣−(1/6)ln(x^2 −x+1)+((√3)/3) arctan(((2x−1)/(√3)))]_(√y) ^2 =(1/3)ln(3)−(1/6)ln(3)+((√3)/3) arctan((√3))−(1/3)ln((√y)+1) +(1/6)ln(y−(√y)+1)−((√3)/3) arctan(((2(√y)−1)/(√3))) ⇒ I =∫_0 ^4 A(y)dy =4{((ln3)/6) +((√3)/3) arctan((√3))}−(1/3)∫_0 ^4 ln(1+(√y))dy +(1/6)∫_0 ^4 ln(y−(√y)+1)dy −((√3)/3) ∫_0 ^4 arctan(((2(√y)−1)/(√3))) we have ∫_0 ^4 ln(1+(√y))dy =_(by parts) [yln(1+(√y))]_0 ^4 −∫_0 ^4 y.(1/(2(√y)(1+(√y))))dy =4ln(3)−(1/2)∫_0 ^4 ((√y)/(1+(√y))) dy (y=t^2 ) =4ln(3)−(1/2) ∫_0 ^2 (t/(1+t))(2t)dt =4ln(3)−∫_0 ^2 (t^2 /(1+t))dt and ∫_0 ^2 (t^2 /(1+t))dt =∫_0 ^2 ((t^2 −1 +1)/(t+1))dt =∫_0 ^2 (t−1)dt +[ln(t+1)]_0 ^2 =[(t^2 /2)−t]_0 ^2 +ln(3) =0+ln(3) =ln(3) ∫_0 ^4 ln(y−(√y)+1)dy =_((√y)=t) ∫_0 ^2 ln(t^2 −t+1)(2t)dt =2 ∫_0 ^2 t ln(t^2 −t+1)dt =_(by parts) 2{ [(t^2 /2)ln(t^2 −t+1)]_0 ^2 −∫_0 ^2 (t^2 /2).((2t−1)/(t^2 −t+1))dt} =2{ 2ln(3)−(1/2) ∫_0 ^2 ((2t^3 −t^2 )/(t^2 −t+1))dt}=....(eazy to solve) also the integral∫_0 ^4 arctan(((2(√y)−1)/(√3))) can be solved by parts ...be continued...](Q106560.png)
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{4}} \:\left(\int_{\sqrt{\mathrm{y}}} ^{\mathrm{2}} \:\frac{\mathrm{dx}}{\mathrm{1}+{x}^{\mathrm{3}} }\right){dy}\:=\int_{\mathrm{0}} ^{\mathrm{4}} \:\mathrm{A}\left(\mathrm{y}\right)\mathrm{dy}\:\mathrm{with}\:\mathrm{A}\left(\mathrm{y}\right)\:=\int_{\sqrt{\mathrm{y}}} ^{\mathrm{2}\:} \:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{3}} \:+\mathrm{1}} \\ $$$$\mathrm{let}\:\mathrm{decompose}\:\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} +\mathrm{1}}\:=\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{a}}{\mathrm{x}+\mathrm{1}}\:+\frac{\mathrm{bx}\:+\mathrm{c}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}\:\:\mathrm{we}\:\mathrm{get}\:\mathrm{a}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{xf}\left(\mathrm{x}\right)\:=\mathrm{0}\:=\mathrm{a}+\mathrm{b}\:\Rightarrow\mathrm{b}\:=−\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{3}\left(\mathrm{x}+\mathrm{1}\right)}+\frac{−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x}+\mathrm{c}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}} \\ $$$$\mathrm{f}\left(\mathrm{0}\right)\:=\mathrm{1}\:=\frac{\mathrm{1}}{\mathrm{3}}\:+\mathrm{c}\:\Rightarrow\mathrm{c}\:=\frac{\mathrm{2}}{\mathrm{3}}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{3}\left(\mathrm{x}+\mathrm{1}\right)}+\frac{−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x}+\frac{\mathrm{2}}{\mathrm{3}}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}} \\ $$$$\Rightarrow\int\:\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\mid\mathrm{x}+\mathrm{1}\mid−\frac{\mathrm{1}}{\mathrm{3}}\int\:\frac{\mathrm{x}−\mathrm{2}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}\mathrm{dx}\:\:\mathrm{but} \\ $$$$\int\:\frac{\mathrm{x}−\mathrm{2}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{2x}−\mathrm{1}−\mathrm{3}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)−\frac{\mathrm{3}}{\mathrm{2}}\int\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}} \\ $$$$\int\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}\mathrm{dx}\:=\int\:\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} −\mathrm{2}\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\:+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{3}}{\mathrm{4}}}\:=\int\:\frac{\mathrm{dx}}{\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$$=_{\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{u}} \:\:\:\frac{\mathrm{4}}{\mathrm{3}}\:\:\int\:\:\:\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}}.\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{du}\:=\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\:\mathrm{arctan}\left(\frac{\mathrm{2x}−\mathrm{1}}{\sqrt{\mathrm{3}}}\right)\:+\mathrm{c}\:\Rightarrow \\ $$$$\int\:\frac{\mathrm{x}−\mathrm{2}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)−\sqrt{\mathrm{3}}\mathrm{arctan}\left(\frac{\mathrm{2x}−\mathrm{1}}{\sqrt{\mathrm{3}}}\right)\:\Rightarrow \\ $$$$\int\:\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\mid\mathrm{x}+\mathrm{1}\mid−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)+\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\:\mathrm{arctan}\left(\frac{\mathrm{2x}−\mathrm{1}}{\sqrt{\mathrm{3}}}\right)\:\Rightarrow \\ $$$$\mathrm{A}\left(\mathrm{y}\right)\:=\left[\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\mid\mathrm{x}+\mathrm{1}\mid−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)+\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\:\mathrm{arctan}\left(\frac{\mathrm{2x}−\mathrm{1}}{\sqrt{\mathrm{3}}}\right)\right]_{\sqrt{\mathrm{y}}} ^{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\left(\mathrm{3}\right)−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln}\left(\mathrm{3}\right)+\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\:\mathrm{arctan}\left(\sqrt{\mathrm{3}}\right)−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\left(\sqrt{\mathrm{y}}+\mathrm{1}\right) \\ $$$$+\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln}\left(\mathrm{y}−\sqrt{\mathrm{y}}+\mathrm{1}\right)−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\:\mathrm{arctan}\left(\frac{\mathrm{2}\sqrt{\mathrm{y}}−\mathrm{1}}{\sqrt{\mathrm{3}}}\right)\:\Rightarrow \\ $$$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{4}} \:\mathrm{A}\left(\mathrm{y}\right)\mathrm{dy}\:=\mathrm{4}\left\{\frac{\mathrm{ln3}}{\mathrm{6}}\:+\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\:\mathrm{arctan}\left(\sqrt{\mathrm{3}}\right)\right\}−\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{4}} \mathrm{ln}\left(\mathrm{1}+\sqrt{\mathrm{y}}\right)\mathrm{dy} \\ $$$$+\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{0}} ^{\mathrm{4}} \mathrm{ln}\left(\mathrm{y}−\sqrt{\mathrm{y}}+\mathrm{1}\right)\mathrm{dy}\:−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\:\int_{\mathrm{0}} ^{\mathrm{4}} \:\mathrm{arctan}\left(\frac{\mathrm{2}\sqrt{\mathrm{y}}−\mathrm{1}}{\sqrt{\mathrm{3}}}\right) \\ $$$$\mathrm{we}\:\mathrm{have}\:\int_{\mathrm{0}} ^{\mathrm{4}} \mathrm{ln}\left(\mathrm{1}+\sqrt{\mathrm{y}}\right)\mathrm{dy}\:=_{\mathrm{by}\:\mathrm{parts}} \:\:\left[\mathrm{yln}\left(\mathrm{1}+\sqrt{\mathrm{y}}\right)\right]_{\mathrm{0}} ^{\mathrm{4}} −\int_{\mathrm{0}} ^{\mathrm{4}} \mathrm{y}.\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{y}}\left(\mathrm{1}+\sqrt{\mathrm{y}}\right)}\mathrm{dy} \\ $$$$=\mathrm{4ln}\left(\mathrm{3}\right)−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{4}} \:\frac{\sqrt{\mathrm{y}}}{\mathrm{1}+\sqrt{\mathrm{y}}}\:\mathrm{dy}\:\:\left(\mathrm{y}=\mathrm{t}^{\mathrm{2}} \right) \\ $$$$=\mathrm{4ln}\left(\mathrm{3}\right)−\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{2}} \:\frac{\mathrm{t}}{\mathrm{1}+\mathrm{t}}\left(\mathrm{2t}\right)\mathrm{dt}\:=\mathrm{4ln}\left(\mathrm{3}\right)−\int_{\mathrm{0}} ^{\mathrm{2}} \:\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}}\mathrm{dt}\:\mathrm{and} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}} \:\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}}\mathrm{dt}\:=\int_{\mathrm{0}} ^{\mathrm{2}} \:\frac{\mathrm{t}^{\mathrm{2}} −\mathrm{1}\:+\mathrm{1}}{\mathrm{t}+\mathrm{1}}\mathrm{dt}\:=\int_{\mathrm{0}} ^{\mathrm{2}} \left(\mathrm{t}−\mathrm{1}\right)\mathrm{dt}\:+\left[\mathrm{ln}\left(\mathrm{t}+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{2}} \\ $$$$=\left[\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{t}\right]_{\mathrm{0}} ^{\mathrm{2}} \:+\mathrm{ln}\left(\mathrm{3}\right)\:=\mathrm{0}+\mathrm{ln}\left(\mathrm{3}\right)\:=\mathrm{ln}\left(\mathrm{3}\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{4}} \mathrm{ln}\left(\mathrm{y}−\sqrt{\mathrm{y}}+\mathrm{1}\right)\mathrm{dy}\:=_{\sqrt{\mathrm{y}}=\mathrm{t}} \:\:\:\int_{\mathrm{0}} ^{\mathrm{2}} \mathrm{ln}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{t}+\mathrm{1}\right)\left(\mathrm{2t}\right)\mathrm{dt} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{2}} \mathrm{t}\:\mathrm{ln}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{t}+\mathrm{1}\right)\mathrm{dt}\:=_{\mathrm{by}\:\mathrm{parts}} \:\mathrm{2}\left\{\:\left[\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}\mathrm{ln}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{t}+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{2}} −\int_{\mathrm{0}} ^{\mathrm{2}} \frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}.\frac{\mathrm{2t}−\mathrm{1}}{\mathrm{t}^{\mathrm{2}} −\mathrm{t}+\mathrm{1}}\mathrm{dt}\right\} \\ $$$$=\mathrm{2}\left\{\:\mathrm{2ln}\left(\mathrm{3}\right)−\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{2}} \:\frac{\mathrm{2t}^{\mathrm{3}} −\mathrm{t}^{\mathrm{2}} }{\mathrm{t}^{\mathrm{2}} −\mathrm{t}+\mathrm{1}}\mathrm{dt}\right\}=....\left(\mathrm{eazy}\:\mathrm{to}\:\mathrm{solve}\right) \\ $$$$\mathrm{also}\:\mathrm{the}\:\mathrm{integral}\int_{\mathrm{0}} ^{\mathrm{4}} \:\mathrm{arctan}\left(\frac{\mathrm{2}\sqrt{\mathrm{y}}−\mathrm{1}}{\sqrt{\mathrm{3}}}\right)\:\mathrm{can}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{by}\:\mathrm{parts} \\ $$$$...\mathrm{be}\:\mathrm{continued}... \\ $$
Commented by Ar Brandon last updated on 06/Aug/20
![May I proceed... ∫_0 ^4 arctan(((2(√y)−1)/(√3)))dy u(y)=arctan(((2(√y)−1)/(√3)))⇒u′(y)=(1/(√(3y)))∙(1/(1+(((2(√y)−1)/(√3)))^2 )) ⇒u′(y)=((√3)/(4(√y)(y−(√y)+1))) v′(y)=1⇒v(y)=y ⇒I=[y∙arctan(((2(√y)−1)/(√3)))]_0 ^4 −((√3)/4)∫_0 ^4 (y/((√y)(y−(√y)+1)))dy =((4π)/3)−((√3)/4)∫_0 ^4 ((√y)/((y−(√y)+1)))dy=((4π)/3)−((√3)/4)∫_0 ^2 ((2t^2 )/(t^2 −t+1))dt =((4π)/3)−((√3)/4)∫_0 ^2 {1+(1/2)∙((t−1)/(t^2 −t+1))}dt =((4π)/3)−((√3)/2)−((√3)/8)∫_0 ^2 {(1/2)∙((2t−1)/(t^2 −t+1))−(1/2)∙(1/(t^2 −t+1))}dt =((4π)/3)−((√3)/2)−[((√3)/(16))ln(t^2 −t+1)]_0 ^2 +((√3)/(16))∫_0 ^2 (dt/((t−(1/2))^2 +(3/4))) =((4π)/3)−((√3)/2)−(((√3)ln3)/(16))+(1/8)[arctan(((2t−1)/(√3)))]_0 ^2 =((4π)/3)−((√3)/2)−(((√3)ln3)/(16))+(1/8)((π/3)+(π/6))](Q106575.png)
$${May}\:{I}\:{proceed}... \\ $$$$ \\ $$$$\int_{\mathrm{0}} ^{\mathrm{4}} \mathrm{arctan}\left(\frac{\mathrm{2}\sqrt{\mathrm{y}}−\mathrm{1}}{\sqrt{\mathrm{3}}}\right)\mathrm{dy} \\ $$$$\mathrm{u}\left(\mathrm{y}\right)=\mathrm{arctan}\left(\frac{\mathrm{2}\sqrt{\mathrm{y}}−\mathrm{1}}{\sqrt{\mathrm{3}}}\right)\Rightarrow\mathrm{u}'\left(\mathrm{y}\right)=\frac{\mathrm{1}}{\sqrt{\mathrm{3y}}}\centerdot\frac{\mathrm{1}}{\mathrm{1}+\left(\frac{\mathrm{2}\sqrt{\mathrm{y}}−\mathrm{1}}{\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{u}'\left(\mathrm{y}\right)=\frac{\sqrt{\mathrm{3}}}{\mathrm{4}\sqrt{\mathrm{y}}\left(\mathrm{y}−\sqrt{\mathrm{y}}+\mathrm{1}\right)} \\ $$$$\mathrm{v}'\left(\mathrm{y}\right)=\mathrm{1}\Rightarrow\mathrm{v}\left(\mathrm{y}\right)=\mathrm{y} \\ $$$$\Rightarrow\mathcal{I}=\left[\mathrm{y}\centerdot\mathrm{arctan}\left(\frac{\mathrm{2}\sqrt{\mathrm{y}}−\mathrm{1}}{\sqrt{\mathrm{3}}}\right)\right]_{\mathrm{0}} ^{\mathrm{4}} −\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{4}} \frac{\mathrm{y}}{\sqrt{\mathrm{y}}\left(\mathrm{y}−\sqrt{\mathrm{y}}+\mathrm{1}\right)}\mathrm{dy} \\ $$$$\:\:\:\:\:\:\:\:=\frac{\mathrm{4}\pi}{\mathrm{3}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{4}} \frac{\sqrt{\mathrm{y}}}{\left(\mathrm{y}−\sqrt{\mathrm{y}}+\mathrm{1}\right)}\mathrm{dy}=\frac{\mathrm{4}\pi}{\mathrm{3}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{2}} \frac{\mathrm{2t}^{\mathrm{2}} }{\mathrm{t}^{\mathrm{2}} −\mathrm{t}+\mathrm{1}}\mathrm{dt} \\ $$$$\:\:\:\:\:\:\:\:=\frac{\mathrm{4}\pi}{\mathrm{3}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{2}} \left\{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\centerdot\frac{\mathrm{t}−\mathrm{1}}{\mathrm{t}^{\mathrm{2}} −\mathrm{t}+\mathrm{1}}\right\}\mathrm{dt} \\ $$$$\:\:\:\:\:\:\:\:=\frac{\mathrm{4}\pi}{\mathrm{3}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{8}}\int_{\mathrm{0}} ^{\mathrm{2}} \left\{\frac{\mathrm{1}}{\mathrm{2}}\centerdot\frac{\mathrm{2t}−\mathrm{1}}{\mathrm{t}^{\mathrm{2}} −\mathrm{t}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}\centerdot\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} −\mathrm{t}+\mathrm{1}}\right\}\mathrm{dt} \\ $$$$\:\:\:\:\:\:\:\:=\frac{\mathrm{4}\pi}{\mathrm{3}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\left[\frac{\sqrt{\mathrm{3}}}{\mathrm{16}}\mathrm{ln}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{t}+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{2}} +\frac{\sqrt{\mathrm{3}}}{\mathrm{16}}\int_{\mathrm{0}} ^{\mathrm{2}} \frac{\mathrm{dt}}{\left(\mathrm{t}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$$\:\:\:\:\:\:\:\:=\frac{\mathrm{4}\pi}{\mathrm{3}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}\mathrm{ln3}}{\mathrm{16}}+\frac{\mathrm{1}}{\mathrm{8}}\left[\mathrm{arctan}\left(\frac{\mathrm{2t}−\mathrm{1}}{\sqrt{\mathrm{3}}}\right)\right]_{\mathrm{0}} ^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:=\frac{\mathrm{4}\pi}{\mathrm{3}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}\mathrm{ln3}}{\mathrm{16}}+\frac{\mathrm{1}}{\mathrm{8}}\left(\frac{\pi}{\mathrm{3}}+\frac{\pi}{\mathrm{6}}\right) \\ $$
Answered by 1549442205PVT last updated on 06/Aug/20
![(1/(1+x^3 ))=(1/((x+1)(x^2 −x+1)))=(a/(x+1))+((bx+c)/(x^2 −x+1)) ⇔(a+b)x^2 +(b−a+c)x+a+c=1 ⇔ { ((a+b=0)),((b−a+c=0)),((a+c=1)) :}⇒ { ((2b+c=0)),((−b+c=1)) :}⇒ { ((b=−1/3)),((c=2/3)),((a=1/3)) :} Hence ∫_(√y) ^( 2) (1/(1+x^3 ))=∫_(√y) ^( 2) (dx/(3(x+1)))−∫_(√y) ^( 2) ((x−2)/(3(x^2 −x+1)))dx =(1/3)ln(x+1)∣_(√y) ^2 −(1/3)((1/2)∫_(√y) ^( 2) ((2x−1−3)/(x^2 −x+1))) =(1/3)(ln3−ln(1+(√y)))−(1/6)∫_(√y) ^( 2) ((d(x^2 −x+1))/((x^2 −x+1)))dx +(1/2)∫_(√y) ^( 2) (dx/(x^2 −x+1))=(1/3)(ln3−ln(1+(√y))) −(1/6)ln(x^2 −x+1)∣_(√y) ^2 +(1/2)×∫ (dx/((x−(1/2))^2 +(((√3)/2))^2 )) ==(1/3)(ln3−ln(1+(√y)))−(1/6)(ln3−ln(y−(√y)+1) +(1/2)×(2/(√3))tan^(−1) (((2x−1)/(√3)))∣_(√y) ^2 =(1/6)ln3+(1/6)ln((y−(√y)+1)/(y+2(√y)+1))+(1/(√3))[(π/3)−tan^(−1) (((2(√y)−1)/(√3)))] Now we calculate I=∫ _0^4 {(1/6)ln3+(1/6)ln((y−(√y)+1)/(y+2(√y)+1))+(1/(√3))[(π/3)−tan^(−1) (((2(√y)−1)/(√3)))]}dy =4((1/6)ln3+(π/(3(√3))))+(1/6)∫_0 ^4 ln((y−(√y)+1)/(y+2(√y)+1))dy −(1/(√3))∫_0 ^( 4) tan^(−1) (((2(√y)−1)/(√3)))dy Now we find A=∫_0 ^4 ln(y−(√y)+1)dy= yln(y−(√y)+1)∣_0 ^4 −∫_0 ^4 y(ln(y−(√y)+1)′dy =4ln3−B B=∫_0 ^4 y.((1−(1/(2(√y))))/(y−(√y)+1))dy=∫_0 ^( 4) ((y(2(√y)−1))/(2(√y)(y−(√y)+1)))dy =(1/2)∫_0 ^( 4) ((2y−(√y))/(y−(√y)+1))dy.Set (√y)=u⇒du=(dy/(2(√y)))=(dy/(2u)) ⇒2udu=dy⇒B=(1/2)∫_0 ^( 2) (((2u^2 −u)2udu)/(u^2 −u+1)) =∫_0 ^( 2) ((2u^3 −u^2 )/(u^2 −u+1))du=∫_0 ^( 2) (2u+((u−2)/(u^2 −u+1)))du =u^2 ∣_0 ^2 +(1/2)∫_0 ^( 2) ((2u−1−3)/(u^2 −u+1))du=u^2 ∣_0 ^2 +(1/2)∫_0 ^( 2) ((d(u^2 −u+1))/(u^2 −u+1))−(3/2)∫_0 ^( 2) (du/((u−(1/2))^2 +(((√3)/2))^2 )) =[u^2 +(1/2)ln(u^2 −u+1)]∣_0 ^2 −(3/2)×(2/(√3))tan^(−1) (((2u−1)/(√3)))∣_0 ^2 =4+(1/2)ln3−(√3) tan^(−1) ((√3))+tan^(−1) (−(1/(√3))) ⇒A=4ln3−B=3.5ln3−4+((π(√3))/3)+(π/6) C=∫ _0^4 ln((√y)+1)^2 dy=2∫_0 ^( 4) ln((√y)+1)dy =2yln((√y)+1)∣_0 ^4 −2∫_0 ^( 4) y.[ln((√y)+1)]′dy =2yln((√y)+1)∣_0 ^4 −D=8ln3−D D=2∫_0 ^( 4) ((y.(1/(2(√y))))/((√y)+1))=∫_0 ^4 ((√y)/((√y)+1))dy=∫_0 ^( 2) ((2u^2 du)/(u+1)) =2∫_0 ^2 (u^2 −1)du+2∫_0 ^2 (du/(u+1))=[2((u^3 /3)−u)+2ln(u+1)]_0 ^2 =2((8/3)−2)+2ln3⇒C=8ln3−D=6ln3−(4/3) Next we calculate E= (1/(√3))∫_0 ^( 4) tan^(−1) (((2(√y)−1)/(√3)))dy Set F=∫_0 ^( 4) tan^(−1) (((2(√y)−1)/(√3))) dy.Putting ((2(√y)−1)/(√3))=u⇒(√y)=(((√3)u+1)/2)⇒y=(3u^2 +2(√3)u+1)/4 ⇒dy=(1/4)(6u+2(√3))du F=∫_0 ^( 4) tan^(−1) (u)×(1/4)(6u+2(√3))du =(3/2)∫_0 ^( 4) utan^(−1) (u)du+((√3)/2)∫_0 ^( 4) tan^(−1) (u)du =(3/4)u^2 tan^(−1) (u)−(3/4)∫_0 ^( 4) ((u^2 du)/(1+u^2 ))+((√3)/2)utan^(−1) (u)−((√3)/2)∫_0 ^( 4) ((udu)/(1+u^2 )) =(3/4)u^2 tan^(−1) (u)−(3/4)∫_0 ^( 4) (1−(1/(1+u^2 )))du +((√3)/2)utan^(−1) (u)−((√3)/4)∫_0 ^( 4) (1/(1+u^2 ))d(u^2 +1) =[(3/4)u^2 tan^(−1) (u)−(3/4)u+(3/4)tan^(−1) (u) +((√3)/2)utan^(−1) (u)−((√3)/4)ln(u^2 +1)]∣_(−(1/(√3))) ^(√3) =(9/4).(π/3)−((3(√3))/4)+(3/4).(π/3)+(3/2).(π/3)−((√3)/4)ln4 −((1/4).((−π)/6)+((√3)/4)−(3/4).(π/6)+(1/2).(π/6)−((√3)/4)ln(4/3)) =((19π)/(12))−(√3)−((√3)/4)ln3⇒E=(1/(√3))F=((19π(√3))/(36))−1−(1/4)ln3 =(1/2)ln3+(((1−(√3))π)/(36))](Q106641.png)
$$ \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\mathrm{3}} }=\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)}=\frac{\mathrm{a}}{\mathrm{x}+\mathrm{1}}+\frac{\mathrm{bx}+\mathrm{c}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}} \\ $$$$\Leftrightarrow\left(\mathrm{a}+\mathrm{b}\right)\mathrm{x}^{\mathrm{2}} +\left(\mathrm{b}−\mathrm{a}+\mathrm{c}\right)\mathrm{x}+\mathrm{a}+\mathrm{c}=\mathrm{1} \\ $$$$\Leftrightarrow\begin{cases}{\mathrm{a}+\mathrm{b}=\mathrm{0}}\\{\mathrm{b}−\mathrm{a}+\mathrm{c}=\mathrm{0}}\\{\mathrm{a}+\mathrm{c}=\mathrm{1}}\end{cases}\Rightarrow\begin{cases}{\mathrm{2b}+\mathrm{c}=\mathrm{0}}\\{−\mathrm{b}+\mathrm{c}=\mathrm{1}}\end{cases}\Rightarrow\begin{cases}{\mathrm{b}=−\mathrm{1}/\mathrm{3}}\\{\mathrm{c}=\mathrm{2}/\mathrm{3}}\\{\mathrm{a}=\mathrm{1}/\mathrm{3}}\end{cases} \\ $$$$\mathrm{Hence}\:\int_{\sqrt{\mathrm{y}}} ^{\:\mathrm{2}} \frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\mathrm{3}} }=\int_{\sqrt{\mathrm{y}}} ^{\:\mathrm{2}} \:\frac{\mathrm{dx}}{\mathrm{3}\left(\mathrm{x}+\mathrm{1}\right)}−\int_{\sqrt{\mathrm{y}}} ^{\:\mathrm{2}} \:\frac{\mathrm{x}−\mathrm{2}}{\mathrm{3}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)}\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\left(\mathrm{x}+\mathrm{1}\right)\mid_{\sqrt{\mathrm{y}}} ^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{2}}\int_{\sqrt{\mathrm{y}}} ^{\:\mathrm{2}} \:\frac{\mathrm{2x}−\mathrm{1}−\mathrm{3}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{ln3}−\mathrm{ln}\left(\mathrm{1}+\sqrt{\mathrm{y}}\right)\right)−\frac{\mathrm{1}}{\mathrm{6}}\int_{\sqrt{\mathrm{y}}} ^{\:\mathrm{2}} \:\frac{\mathrm{d}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)}\mathrm{dx} \\ $$$$+\frac{\mathrm{1}}{\mathrm{2}}\int_{\sqrt{\mathrm{y}}} ^{\:\mathrm{2}} \:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{ln3}−\mathrm{ln}\left(\mathrm{1}+\sqrt{\mathrm{y}}\right)\right) \\ $$$$−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)\mid_{\sqrt{\mathrm{y}}} ^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}×\int\:\frac{\mathrm{dx}}{\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$==\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{ln3}−\mathrm{ln}\left(\mathrm{1}+\sqrt{\mathrm{y}}\right)\right)−\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{ln3}−\mathrm{ln}\left(\mathrm{y}−\sqrt{\mathrm{y}}+\mathrm{1}\right)\right. \\ $$$$+\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2x}−\mathrm{1}}{\sqrt{\mathrm{3}}}\right)\mid_{\sqrt{\mathrm{y}}} ^{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln3}+\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln}\frac{\mathrm{y}−\sqrt{\mathrm{y}}+\mathrm{1}}{\mathrm{y}+\mathrm{2}\sqrt{\mathrm{y}}+\mathrm{1}}+\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\left[\frac{\pi}{\mathrm{3}}−\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}\sqrt{\mathrm{y}}−\mathrm{1}}{\sqrt{\mathrm{3}}}\right)\right] \\ $$$$\mathrm{Now}\:\mathrm{we}\:\mathrm{calculate} \\ $$$$\mathrm{I}=\int\:_{\mathrm{0}} ^{\mathrm{4}} \left\{\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln3}+\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln}\frac{\mathrm{y}−\sqrt{\mathrm{y}}+\mathrm{1}}{\mathrm{y}+\mathrm{2}\sqrt{\mathrm{y}}+\mathrm{1}}+\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\left[\frac{\pi}{\mathrm{3}}−\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}\sqrt{\mathrm{y}}−\mathrm{1}}{\sqrt{\mathrm{3}}}\right)\right]\right\}\mathrm{dy} \\ $$$$=\mathrm{4}\left(\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln3}+\frac{\pi}{\mathrm{3}\sqrt{\mathrm{3}}}\right)+\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{0}} ^{\mathrm{4}} \mathrm{ln}\frac{\mathrm{y}−\sqrt{\mathrm{y}}+\mathrm{1}}{\mathrm{y}+\mathrm{2}\sqrt{\mathrm{y}}+\mathrm{1}}\mathrm{dy} \\ $$$$−\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\int_{\mathrm{0}} ^{\:\mathrm{4}} \mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}\sqrt{\mathrm{y}}−\mathrm{1}}{\sqrt{\mathrm{3}}}\right)\mathrm{dy} \\ $$$$\mathrm{Now}\:\mathrm{we}\:\mathrm{find}\:\mathrm{A}=\int_{\mathrm{0}} ^{\mathrm{4}} \mathrm{ln}\left(\mathrm{y}−\sqrt{\mathrm{y}}+\mathrm{1}\right)\mathrm{dy}= \\ $$$$\mathrm{yln}\left(\mathrm{y}−\sqrt{\mathrm{y}}+\mathrm{1}\right)\mid_{\mathrm{0}} ^{\mathrm{4}} −\int_{\mathrm{0}} ^{\mathrm{4}} \mathrm{y}\left(\mathrm{ln}\left(\mathrm{y}−\sqrt{\mathrm{y}}+\mathrm{1}\right)'\mathrm{dy}\right. \\ $$$$=\mathrm{4ln3}−\mathrm{B} \\ $$$$\mathrm{B}=\int_{\mathrm{0}} ^{\mathrm{4}} \:\mathrm{y}.\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{y}}}}{\mathrm{y}−\sqrt{\mathrm{y}}+\mathrm{1}}\mathrm{dy}=\int_{\mathrm{0}} ^{\:\mathrm{4}} \frac{\mathrm{y}\left(\mathrm{2}\sqrt{\mathrm{y}}−\mathrm{1}\right)}{\mathrm{2}\sqrt{\mathrm{y}}\left(\mathrm{y}−\sqrt{\mathrm{y}}+\mathrm{1}\right)}\mathrm{dy} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{4}} \frac{\mathrm{2y}−\sqrt{\mathrm{y}}}{\mathrm{y}−\sqrt{\mathrm{y}}+\mathrm{1}}\mathrm{dy}.\mathrm{Set}\:\sqrt{\mathrm{y}}=\mathrm{u}\Rightarrow\mathrm{du}=\frac{\mathrm{dy}}{\mathrm{2}\sqrt{\mathrm{y}}}=\frac{\mathrm{dy}}{\mathrm{2u}} \\ $$$$\Rightarrow\mathrm{2udu}=\mathrm{dy}\Rightarrow\mathrm{B}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{2}} \:\frac{\left(\mathrm{2u}^{\mathrm{2}} −\mathrm{u}\right)\mathrm{2udu}}{\mathrm{u}^{\mathrm{2}} −\mathrm{u}+\mathrm{1}} \\ $$$$=\int_{\mathrm{0}} ^{\:\mathrm{2}} \:\frac{\mathrm{2u}^{\mathrm{3}} −\mathrm{u}^{\mathrm{2}} }{\mathrm{u}^{\mathrm{2}} −\mathrm{u}+\mathrm{1}}\mathrm{du}=\int_{\mathrm{0}} ^{\:\mathrm{2}} \left(\mathrm{2u}+\frac{\mathrm{u}−\mathrm{2}}{\mathrm{u}^{\mathrm{2}} −\mathrm{u}+\mathrm{1}}\right)\mathrm{du} \\ $$$$=\mathrm{u}^{\mathrm{2}} \mid_{\mathrm{0}} ^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{2}} \:\:\frac{\mathrm{2u}−\mathrm{1}−\mathrm{3}}{\mathrm{u}^{\mathrm{2}} −\mathrm{u}+\mathrm{1}}\mathrm{du}=\mathrm{u}^{\mathrm{2}} \mid_{\mathrm{0}} ^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{2}} \:\frac{\mathrm{d}\left(\mathrm{u}^{\mathrm{2}} −\mathrm{u}+\mathrm{1}\right)}{\mathrm{u}^{\mathrm{2}} −\mathrm{u}+\mathrm{1}}−\frac{\mathrm{3}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{2}} \:\frac{\mathrm{du}}{\left(\mathrm{u}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$=\left[\mathrm{u}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{u}^{\mathrm{2}} −\mathrm{u}+\mathrm{1}\right)\right]\mid_{\mathrm{0}} ^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{2}}×\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2u}−\mathrm{1}}{\sqrt{\mathrm{3}}}\right)\mid_{\mathrm{0}} ^{\mathrm{2}} \\ $$$$=\mathrm{4}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln3}−\sqrt{\mathrm{3}}\:\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\mathrm{3}}\right)+\mathrm{tan}^{−\mathrm{1}} \left(−\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\right) \\ $$$$\Rightarrow\mathrm{A}=\mathrm{4ln3}−\mathrm{B}=\mathrm{3}.\mathrm{5ln3}−\mathrm{4}+\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{3}}+\frac{\pi}{\mathrm{6}} \\ $$$$\mathrm{C}=\int\:_{\mathrm{0}} ^{\mathrm{4}} \:\mathrm{ln}\left(\sqrt{\mathrm{y}}+\mathrm{1}\right)^{\mathrm{2}} \mathrm{dy}=\mathrm{2}\int_{\mathrm{0}} ^{\:\mathrm{4}} \mathrm{ln}\left(\sqrt{\mathrm{y}}+\mathrm{1}\right)\mathrm{dy} \\ $$$$=\mathrm{2yln}\left(\sqrt{\mathrm{y}}+\mathrm{1}\right)\mid_{\mathrm{0}} ^{\mathrm{4}} −\mathrm{2}\int_{\mathrm{0}} ^{\:\mathrm{4}} \mathrm{y}.\left[\mathrm{ln}\left(\sqrt{\mathrm{y}}+\mathrm{1}\right)\right]'\mathrm{dy} \\ $$$$=\mathrm{2yln}\left(\sqrt{\mathrm{y}}+\mathrm{1}\right)\mid_{\mathrm{0}} ^{\mathrm{4}} −\mathrm{D}=\mathrm{8ln3}−\mathrm{D} \\ $$$$\mathrm{D}=\mathrm{2}\int_{\mathrm{0}} ^{\:\mathrm{4}} \:\frac{\mathrm{y}.\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{y}}}}{\sqrt{\mathrm{y}}+\mathrm{1}}=\int_{\mathrm{0}} ^{\mathrm{4}} \frac{\sqrt{\mathrm{y}}}{\sqrt{\mathrm{y}}+\mathrm{1}}\mathrm{dy}=\int_{\mathrm{0}} ^{\:\mathrm{2}} \:\frac{\mathrm{2u}^{\mathrm{2}} \mathrm{du}}{\mathrm{u}+\mathrm{1}} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{2}} \left(\mathrm{u}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{du}+\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{2}} \:\frac{\mathrm{du}}{\mathrm{u}+\mathrm{1}}=\left[\mathrm{2}\left(\frac{\mathrm{u}^{\mathrm{3}} }{\mathrm{3}}−\mathrm{u}\right)+\mathrm{2ln}\left(\mathrm{u}+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{2}} \\ $$$$=\mathrm{2}\left(\frac{\mathrm{8}}{\mathrm{3}}−\mathrm{2}\right)+\mathrm{2ln3}\Rightarrow\mathrm{C}=\mathrm{8ln3}−\mathrm{D}=\mathrm{6ln3}−\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$\mathrm{Next}\:\mathrm{we}\:\mathrm{calculate}\:\mathrm{E}=\:\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\int_{\mathrm{0}} ^{\:\mathrm{4}} \mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}\sqrt{\mathrm{y}}−\mathrm{1}}{\sqrt{\mathrm{3}}}\right)\mathrm{dy} \\ $$$$\mathrm{Set}\:\mathrm{F}=\int_{\mathrm{0}} ^{\:\mathrm{4}} \mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}\sqrt{\mathrm{y}}−\mathrm{1}}{\sqrt{\mathrm{3}}}\right)\:\mathrm{dy}.\mathrm{Putting} \\ $$$$\frac{\mathrm{2}\sqrt{\mathrm{y}}−\mathrm{1}}{\sqrt{\mathrm{3}}}=\mathrm{u}\Rightarrow\sqrt{\mathrm{y}}=\frac{\sqrt{\mathrm{3}}\mathrm{u}+\mathrm{1}}{\mathrm{2}}\Rightarrow\mathrm{y}=\left(\mathrm{3u}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{3}}\mathrm{u}+\mathrm{1}\right)/\mathrm{4} \\ $$$$\Rightarrow\mathrm{dy}=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{6u}+\mathrm{2}\sqrt{\mathrm{3}}\right)\mathrm{du} \\ $$$$\mathrm{F}=\int_{\mathrm{0}} ^{\:\mathrm{4}} \mathrm{tan}^{−\mathrm{1}} \left(\mathrm{u}\right)×\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{6u}+\mathrm{2}\sqrt{\mathrm{3}}\right)\mathrm{du} \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{4}} \:\mathrm{utan}^{−\mathrm{1}} \left(\mathrm{u}\right)\mathrm{du}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{4}} \mathrm{tan}^{−\mathrm{1}} \left(\mathrm{u}\right)\mathrm{du} \\ $$$$=\frac{\mathrm{3}}{\mathrm{4}}\mathrm{u}^{\mathrm{2}} \mathrm{tan}^{−\mathrm{1}} \left(\mathrm{u}\right)−\frac{\mathrm{3}}{\mathrm{4}}\int_{\mathrm{0}} ^{\:\mathrm{4}} \:\frac{\mathrm{u}^{\mathrm{2}} \mathrm{du}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{utan}^{−\mathrm{1}} \left(\mathrm{u}\right)−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{4}} \:\frac{\mathrm{udu}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{3}}{\mathrm{4}}\mathrm{u}^{\mathrm{2}} \mathrm{tan}^{−\mathrm{1}} \left(\mathrm{u}\right)−\frac{\mathrm{3}}{\mathrm{4}}\int_{\mathrm{0}} ^{\:\mathrm{4}} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\right)\mathrm{du} \\ $$$$+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{utan}^{−\mathrm{1}} \left(\mathrm{u}\right)−\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\int_{\mathrm{0}} ^{\:\mathrm{4}} \frac{\mathrm{1}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\mathrm{d}\left(\mathrm{u}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$=\left[\frac{\mathrm{3}}{\mathrm{4}}\mathrm{u}^{\mathrm{2}} \mathrm{tan}^{−\mathrm{1}} \left(\mathrm{u}\right)−\frac{\mathrm{3}}{\mathrm{4}}\mathrm{u}+\frac{\mathrm{3}}{\mathrm{4}}\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{u}\right)\right. \\ $$$$\left.+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{utan}^{−\mathrm{1}} \left(\mathrm{u}\right)−\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\mathrm{ln}\left(\mathrm{u}^{\mathrm{2}} +\mathrm{1}\right)\right]\mid_{−\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}} ^{\sqrt{\mathrm{3}}} \\ $$$$=\frac{\mathrm{9}}{\mathrm{4}}.\frac{\pi}{\mathrm{3}}−\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{4}}+\frac{\mathrm{3}}{\mathrm{4}}.\frac{\pi}{\mathrm{3}}+\frac{\mathrm{3}}{\mathrm{2}}.\frac{\pi}{\mathrm{3}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\mathrm{ln4} \\ $$$$−\left(\frac{\mathrm{1}}{\mathrm{4}}.\frac{−\pi}{\mathrm{6}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}−\frac{\mathrm{3}}{\mathrm{4}}.\frac{\pi}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{2}}.\frac{\pi}{\mathrm{6}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\mathrm{ln}\frac{\mathrm{4}}{\mathrm{3}}\right) \\ $$$$=\frac{\mathrm{19}\pi}{\mathrm{12}}−\sqrt{\mathrm{3}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\mathrm{ln3}\Rightarrow\mathrm{E}=\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\mathrm{F}=\frac{\mathrm{19}\pi\sqrt{\mathrm{3}}}{\mathrm{36}}−\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln3} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln3}+\frac{\left(\mathrm{1}−\sqrt{\mathrm{3}}\right)\pi}{\mathrm{36}} \\ $$