Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 106591 by mathdave last updated on 06/Aug/20

Commented by Her_Majesty last updated on 06/Aug/20

$$\mathrm{\infty }isnotanumber$$$$\underset{x\to \mathrm{\infty }}{limx}!\ne \sqrt{2\pi }$$

Commented by mathdave last updated on 06/Aug/20

$$yesbutcanbprove$$

Commented by Her_Majesty last updated on 06/Aug/20

$${it}^{\prime }ssimplywrong.$$$$x!\approx {\left(\frac{x}{\mathrm{e}}\right)}^x\sqrt{2\pi x}forx\to +\mathrm{\infty }wegetx!\to +\mathrm{\infty }$$

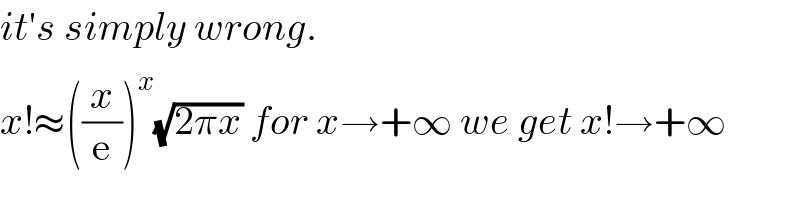
Commented by Her_Majesty last updated on 07/Aug/20

$$I^{\prime }mnotaSir\mathrm{beware}!!!I^{\prime }maLady$$

Commented by Ar Brandon last updated on 07/Aug/20

Lol, don't bother yourself Sir. I know you wouldn't like to draw the others' attention��

Commented by Her_Majesty last updated on 07/Aug/20

$$whatareyoutalkingabout?$$

Commented by Ar Brandon last updated on 07/Aug/20

Deleted��

Answered by Ar Brandon last updated on 06/Aug/20

$${\mathrm{A}}_{\mathrm{n}}=\underset{\mathrm{n}\to \mathrm{\infty }}{\lim n}!\Rightarrow {\mathrm{lnA}}_{\mathrm{n}}=\underset{\mathrm{n}\to \mathrm{\infty }}{\lim ln}(\mathrm{n}!)=\underset{\mathrm{n}\to \mathrm{\infty }}{\lim ln}\underset{\mathrm{k}=0}{\prod ^{\mathrm{n}-1}}(\mathrm{n}-\mathrm{k})$$$${\mathrm{lnA}}_{\mathrm{n}}=\underset{\mathrm{n}\to \mathrm{\infty }}{\lim }\underset{\mathrm{k}=0}{\sum ^{\mathrm{n}-1}}\ln (\mathrm{n}-\mathrm{k})=\underset{\mathrm{n}\to \mathrm{\infty }}{\lim n}\cdot \frac{1}{\mathrm{n}}\underset{\mathrm{k}=0}{\sum ^{\mathrm{n}-1}}\ln \left(\mathrm{n}(1-\frac{\mathrm{k}}{\mathrm{n}})\right)$$$$=\underset{\mathrm{n}\to \mathrm{\infty }}{\lim n}{\int }_0^1\ln \left(\mathrm{n}(1-\mathrm{x})\right)\mathrm{dx}=\underset{\mathrm{n}\to \mathrm{\infty }}{\lim n}{\int }_0^1\ln \left(\mathrm{tn}\right)\mathrm{dt}$$$$=\underset{\mathrm{n}\to \mathrm{\infty }}{\lim }{\left\{\mathrm{tn}(\ln \left(\mathrm{tn}\right)-1)\right\}}_0^1=\underset{\mathrm{n}\to \mathrm{\infty }}{\lim }\{\mathrm{n}(\ln \left(\mathrm{n}\right)-1\}=+\mathrm{\infty }$$$${\mathrm{A}}_{\mathrm{n}}={\mathrm{e}}^{+\mathrm{\infty }}\ne \sqrt{2\pi }$$$$$$$$Ifeeltheremaybeaproblemwiththisquestion.$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com