Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 106614 by bemath last updated on 06/Aug/20

_(@bemath@) lim_(x→0) ((((1+3sin x ))^(1/3) −((1+sin 3x))^(1/3) )/(2x)) =?

$$\:\:\:\:\:\underset{@\mathrm{bemath}@} {\:} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{3sin}\:\mathrm{x}\:}\:−\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{sin}\:\mathrm{3x}}}{\mathrm{2x}}\:=?\: \\ $$

Answered by Dwaipayan Shikari last updated on 06/Aug/20

lim_(x→0) ((1+sinx−1−((sin3x)/3))/(2x))=((x−(x^3 /(3!))−((3x)/3)+(((3x)^3 )/(3.3!)))/(2x))=((((9x^3 )/6)−(x^3 /6))/(2x))=((4x^2 )/6)=0

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}+{sinx}−\mathrm{1}−\frac{{sin}\mathrm{3}{x}}{\mathrm{3}}}{\mathrm{2}{x}}=\frac{{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}−\frac{\mathrm{3}{x}}{\mathrm{3}}+\frac{\left(\mathrm{3}{x}\right)^{\mathrm{3}} }{\mathrm{3}.\mathrm{3}!}}{\mathrm{2}{x}}=\frac{\frac{\mathrm{9}{x}^{\mathrm{3}} }{\mathrm{6}}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}}{\mathrm{2}{x}}=\frac{\mathrm{4}{x}^{\mathrm{2}} }{\mathrm{6}}=\mathrm{0} \\ $$

Commented by bemath last updated on 06/Aug/20

sin x = x−(x^3 /(3!))+...?

$$\mathrm{sin}\:\mathrm{x}\:=\:\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}!}+...? \\ $$

Commented by Dwaipayan Shikari last updated on 06/Aug/20

Oh i edited my error

$${Oh}\:{i}\:{edited}\:{my}\:{error} \\ $$

Commented by bemath last updated on 06/Aug/20

thank you

$$\mathrm{thank}\:\mathrm{you} \\ $$

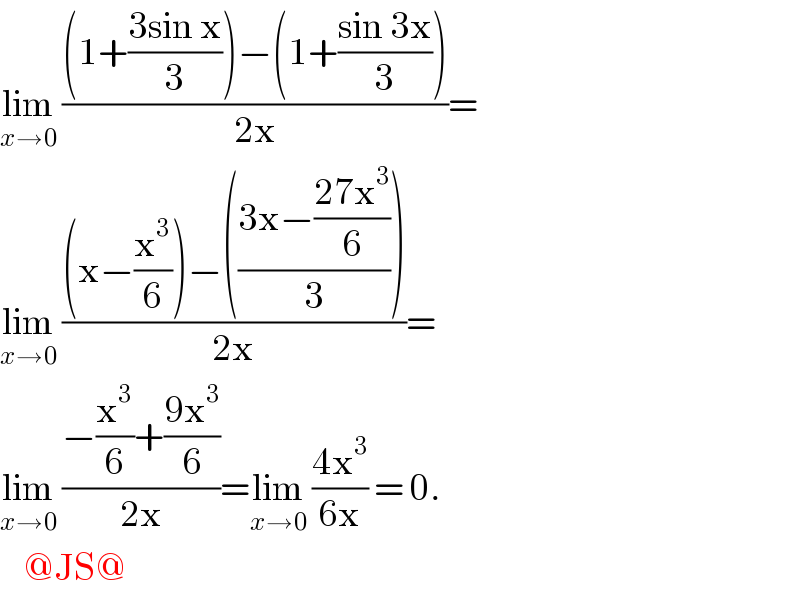
Answered by john santu last updated on 06/Aug/20

lim_(x→0) (((1+((3sin x)/3))−(1+((sin 3x)/3)))/(2x))= lim_(x→0) (((x−(x^3 /6))−(((3x−((27x^3 )/6))/3)))/(2x))= lim_(x→0) ((−(x^3 /6)+((9x^3 )/6))/(2x))=lim_(x→0) ((4x^3 )/(6x)) = 0. @JS@

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{1}+\frac{\mathrm{3sin}\:\mathrm{x}}{\mathrm{3}}\right)−\left(\mathrm{1}+\frac{\mathrm{sin}\:\mathrm{3x}}{\mathrm{3}}\right)}{\mathrm{2x}}= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}\right)−\left(\frac{\mathrm{3x}−\frac{\mathrm{27x}^{\mathrm{3}} }{\mathrm{6}}}{\mathrm{3}}\right)}{\mathrm{2x}}= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}+\frac{\mathrm{9x}^{\mathrm{3}} }{\mathrm{6}}}{\mathrm{2x}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{4x}^{\mathrm{3}} }{\mathrm{6x}}\:=\:\mathrm{0}. \\ $$$$\:\:\:\:@\mathrm{JS}@ \\ $$

Answered by 1549442205PVT last updated on 06/Aug/20

Multiplying nominator and deminator by conjulate expression we get ((((1+3sin x ))^(1/3) −((1+sin 3x))^(1/3) )/(2x)) =(((1−3sinx)−(1+sin3x))/(x[(^3 (√(1+3sinx)))^2 +^3 (√((1+3sinx)(1+sin3x)))+(^3 (√(1+sin3x)))^2 ])) ==((3sinx−sin3x)/(x[(^3 (√(1+3sinx)))^2 +^3 (√((1+3sinx)(1+sin3x)))+(^3 (√(1+sin3x)))^2 ])) =(([3sinx−(3sinx−4sin^3 x])/(x[(^3 (√(1+3sinx)))^2 +^3 (√((1+3sinx)(1+sin3x)))+(^3 (√(1+sin3x)))^2 ])) =((sinx)/x)×((4sin^2 x)/(x[(^3 (√(1+3sinx)))^2 +^3 (√((1+3sinx)(1+sin3x)))+(^3 (√(1+sin3x)))^2 ])) Hence,lim_(x→0) ((((1+3sin x ))^(1/3) −((1+sin 3x))^(1/3) )/(2x))= lim_(x→0) =((sinx)/x)×((4sin^2 x)/([(^3 (√(1+3sinx)))^2 +^3 (√((1+3sinx)(1+sin3x)))+(^3 (√(1+sin3x)))^2 ])) =1×(0/(1+1+1))=0

$$\:\mathrm{Multiplying}\:\mathrm{nominator}\:\mathrm{and}\:\mathrm{deminator}\:\mathrm{by}\:\mathrm{conjulate}\:\mathrm{expression}\:\mathrm{we}\:\mathrm{get} \\ $$$$\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{3sin}\:\mathrm{x}\:}\:−\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{sin}\:\mathrm{3x}}}{\mathrm{2x}}\: \\ $$$$=\frac{\left(\mathrm{1}−\mathrm{3sinx}\right)−\left(\mathrm{1}+\mathrm{sin3x}\right)}{\mathrm{x}\left[\left(\:^{\mathrm{3}} \sqrt{\mathrm{1}+\mathrm{3sinx}}\right)^{\mathrm{2}} +\:^{\mathrm{3}} \sqrt{\left(\mathrm{1}+\mathrm{3sinx}\right)\left(\mathrm{1}+\mathrm{sin3x}\right)}+\left(\:^{\mathrm{3}} \sqrt{\mathrm{1}+\mathrm{sin3x}}\right)^{\mathrm{2}} \right]} \\ $$$$==\frac{\mathrm{3sinx}−\mathrm{sin3x}}{\mathrm{x}\left[\left(\:^{\mathrm{3}} \sqrt{\mathrm{1}+\mathrm{3sinx}}\right)^{\mathrm{2}} +\:^{\mathrm{3}} \sqrt{\left(\mathrm{1}+\mathrm{3sinx}\right)\left(\mathrm{1}+\mathrm{sin3x}\right)}+\left(\:^{\mathrm{3}} \sqrt{\mathrm{1}+\mathrm{sin3x}}\right)^{\mathrm{2}} \right]} \\ $$$$=\frac{\left[\mathrm{3sinx}−\left(\mathrm{3sinx}−\mathrm{4sin}^{\mathrm{3}} \mathrm{x}\right]\right.}{\mathrm{x}\left[\left(\:^{\mathrm{3}} \sqrt{\mathrm{1}+\mathrm{3sinx}}\right)^{\mathrm{2}} +\:^{\mathrm{3}} \sqrt{\left(\mathrm{1}+\mathrm{3sinx}\right)\left(\mathrm{1}+\mathrm{sin3x}\right)}+\left(\:^{\mathrm{3}} \sqrt{\mathrm{1}+\mathrm{sin3x}}\right)^{\mathrm{2}} \right]} \\ $$$$=\frac{\mathrm{sinx}}{\mathrm{x}}×\frac{\mathrm{4sin}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}\left[\left(\:^{\mathrm{3}} \sqrt{\mathrm{1}+\mathrm{3sinx}}\right)^{\mathrm{2}} +\:^{\mathrm{3}} \sqrt{\left(\mathrm{1}+\mathrm{3sinx}\right)\left(\mathrm{1}+\mathrm{sin3x}\right)}+\left(\:^{\mathrm{3}} \sqrt{\mathrm{1}+\mathrm{sin3x}}\right)^{\mathrm{2}} \right]} \\ $$$$\mathrm{Hence},\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{3sin}\:\mathrm{x}\:}\:−\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{sin}\:\mathrm{3x}}}{\mathrm{2x}}= \\ $$$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}=\frac{\mathrm{sinx}}{\mathrm{x}}×\frac{\mathrm{4sin}^{\mathrm{2}} \mathrm{x}}{\left[\left(\:^{\mathrm{3}} \sqrt{\mathrm{1}+\mathrm{3sinx}}\right)^{\mathrm{2}} +\:^{\mathrm{3}} \sqrt{\left(\mathrm{1}+\mathrm{3sinx}\right)\left(\mathrm{1}+\mathrm{sin3x}\right)}+\left(\:^{\mathrm{3}} \sqrt{\mathrm{1}+\mathrm{sin3x}}\right)^{\mathrm{2}} \right]} \\ $$$$=\mathrm{1}×\frac{\mathrm{0}}{\mathrm{1}+\mathrm{1}+\mathrm{1}}=\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com