
Question and Answers Forum
Question Number 106695 by bobhans last updated on 06/Aug/20
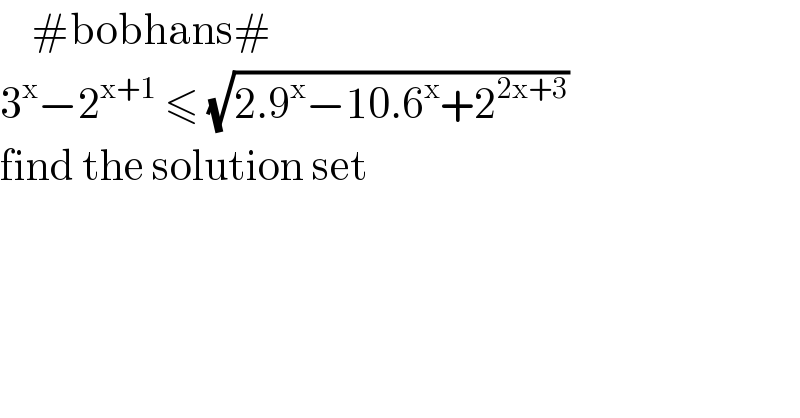
Answered by bemath last updated on 06/Aug/20
![^(@bemath@) ((3^x −2.2^x )/2^x ) ≤ ((√(2.9^x −10.6^x +8.(2^x )^2 ))/2^x ) ((3/2))^x −2 ≤ (√(2((3/2))^(2x) −10((3/2))^x +8)) set ((3/2))^x = t t−2 ≤ (√(2(t−1)(t−4))) defined on (t−1)(t−4)≥0 ⇒ t ≤1 ∪ t ≥ 4...(1) squaring both sides t^2 −4t+4 ≤ 2t^2 −10t+8 −t^2 +6t−4 ≤ 0 ; t^2 −6t+4 ≥ 0 (t−3)^2 −5≥0 t≤3−(√5) ∪t ≥ 3+(√5) ...(2) from (1)∩(2) we get → { ((t ≤1)),((t≥3+(√5))) :} { ((((3/2))^x ≤1 ⇒ x ≤ 0)),((((3/2))^x ≥ 3+(√5) ⇒x ≥log _(((3/2))) (3+(√5)) )) :} the solution set is x∈(−∞,0 ] ∪ [ log _(((3/2))) (3+(√5)) ,∞ )](Q106697.png)
Commented by bobhans last updated on 06/Aug/20

| ||
Question and Answers Forum | ||
Question Number 106695 by bobhans last updated on 06/Aug/20 | ||
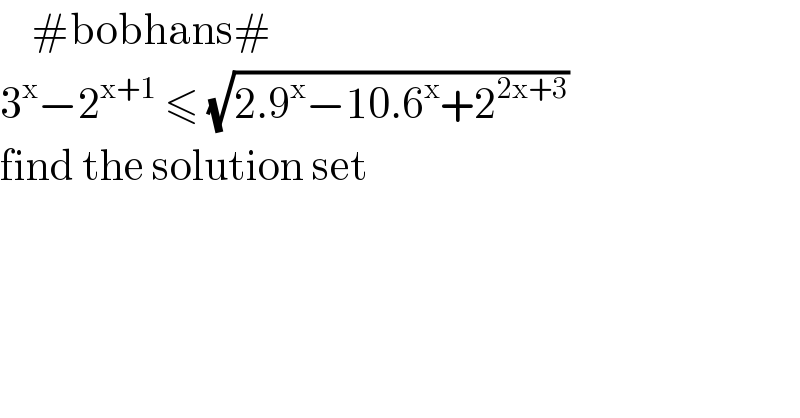 | ||
Answered by bemath last updated on 06/Aug/20 | ||
![^(@bemath@) ((3^x −2.2^x )/2^x ) ≤ ((√(2.9^x −10.6^x +8.(2^x )^2 ))/2^x ) ((3/2))^x −2 ≤ (√(2((3/2))^(2x) −10((3/2))^x +8)) set ((3/2))^x = t t−2 ≤ (√(2(t−1)(t−4))) defined on (t−1)(t−4)≥0 ⇒ t ≤1 ∪ t ≥ 4...(1) squaring both sides t^2 −4t+4 ≤ 2t^2 −10t+8 −t^2 +6t−4 ≤ 0 ; t^2 −6t+4 ≥ 0 (t−3)^2 −5≥0 t≤3−(√5) ∪t ≥ 3+(√5) ...(2) from (1)∩(2) we get → { ((t ≤1)),((t≥3+(√5))) :} { ((((3/2))^x ≤1 ⇒ x ≤ 0)),((((3/2))^x ≥ 3+(√5) ⇒x ≥log _(((3/2))) (3+(√5)) )) :} the solution set is x∈(−∞,0 ] ∪ [ log _(((3/2))) (3+(√5)) ,∞ )](Q106697.png) | ||
| ||
Commented by bobhans last updated on 06/Aug/20 | ||
 | ||