
Question and Answers Forum
Question Number 106830 by malwaan last updated on 08/Aug/20
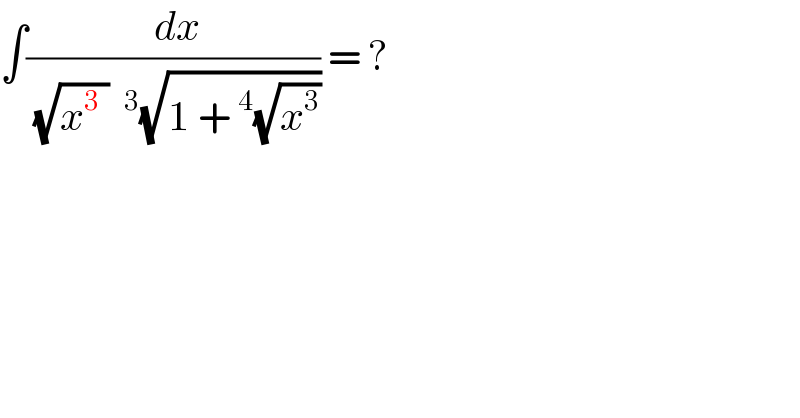
Commented by mathmax by abdo last updated on 07/Aug/20
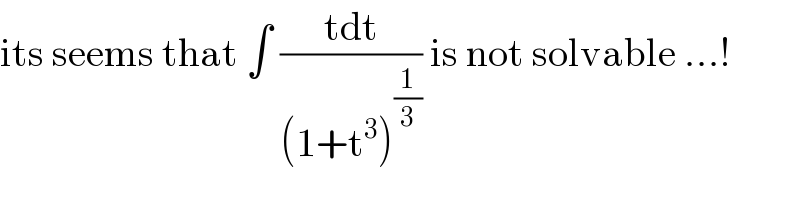
Commented by bobhans last updated on 07/Aug/20
![∫ (dx/((x^2 )^(1/4) ((1+(x^3 )^(1/4) ))^(1/3) )) [ let (x)^(1/4) = t ] ∫ ((4t^3 dt)/(t^2 ((1+t^3 ))^(1/3) )) = ∫ ((4t)/((1+t^3 ))^(1/3) ) dt next...](Q106839.png)
Commented by Her_Majesty last updated on 07/Aug/20
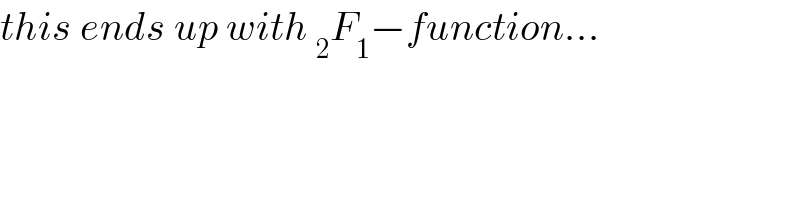
Commented by malwaan last updated on 07/Aug/20
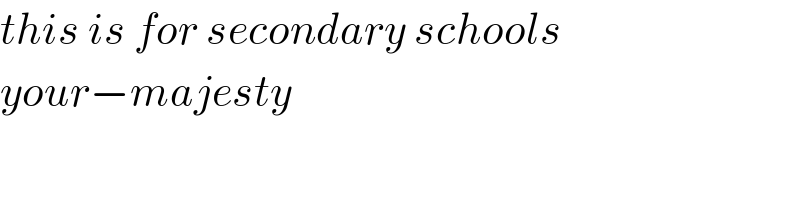
Commented by Sarah85 last updated on 07/Aug/20
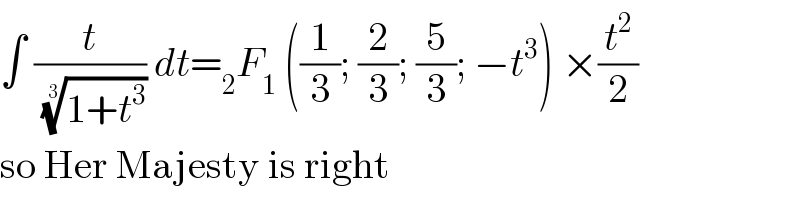
Commented by malwaan last updated on 08/Aug/20

Commented by malwaan last updated on 08/Aug/20
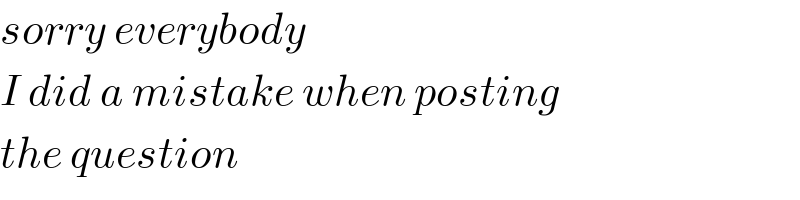
Answered by malwaan last updated on 08/Aug/20
![I= ∫ x^(−(2/3)) (1+x^(3/4) )^(−(1/3)) dx t=(((1+x^(3/4) )/x^(3/4) ))^(1/3) =(1+x^(−(3/4)) ) t^3 =1+x^(−(3/4)) x^(−(3/4)) = t^3 −1 ; x^(3/4) = (1/(t^3 −1)) x = (t^3 −1)^(−(4/3)) ⇒dx = −4t^2 (t^3 −1)^(−(7/3)) dt ∫[(t^3 −1)^(−(4/3)) ]^(−(3/2)) [1+(1/(t^3 −1))]^(−(1/3)) (−4t^2 )(t^3 −1)^(−(7/3)) dt = −4∫ t^2 (t^3 −1)^2 t^(−1) (t^3 −1)^(1/3) (t^3 −1)^(−(7/3)) dt = −4∫ tdt = −4(t^2 /2) + C = −2t^2 + C = −2 ^3 (√((1+ x^(−(3/4)) )^2 )) + C](Q106981.png)
