Question Number 106867 by Penguin last updated on 07/Aug/20
$$\forall{n}\in\left(\mathrm{0},\:\mathrm{1}\right)\forall{x}\in\mathbb{R}\::\:{f}\left({x}\right)\:=\:\frac{{n}}{{n}−\mathrm{1}}{x}+{n} \\ $$$$\mathrm{The}\:\mathrm{given}\:\mathrm{function}\:\mathrm{gives}\:\mathrm{a}\:\mathrm{linear}\:\mathrm{line}\:\mathrm{that} \\ $$$$\mathrm{goes}\:\mathrm{through}\:\mathrm{points}\:\left(\mathrm{0},\:{n}\right)\:\mathrm{and}\:\left(\mathrm{1}−{n},\:\mathrm{0}\right). \\ $$$$\mathrm{The}\:\mathrm{function}\:\mathrm{changes}\:\mathrm{as}\:{n}\:\mathrm{changes}. \\ $$$$\mathrm{What}\:\mathrm{area}\:\mathrm{is}\:\mathrm{beneath}\:\mathrm{the}\:\mathrm{shape}\:\mathrm{made}\:\mathrm{as} \\ $$$${n}\:\mathrm{goes}\:\mathrm{from}\:\mathrm{0}\rightarrow\mathrm{1}? \\ $$
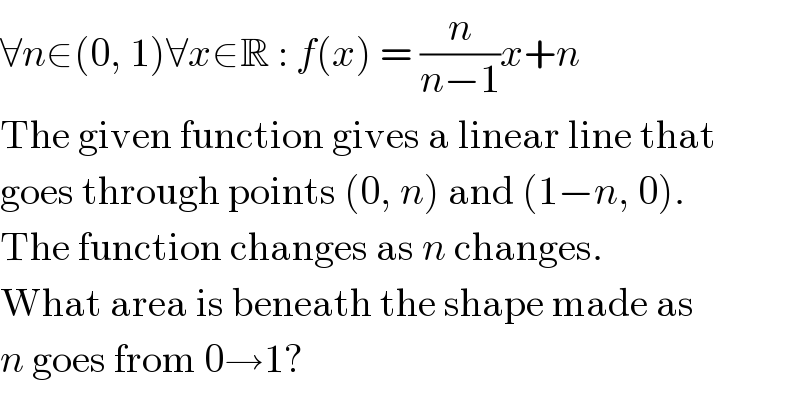
Commented by Penguin last updated on 07/Aug/20
$$\mathrm{Is}\:\mathrm{the}\:\mathrm{solution}: \\ $$$${A}=\int_{\mathrm{0}} ^{\:\mathrm{1}} \int_{\mathrm{0}} ^{\:\mathrm{1}} {f}\:{dxdn}\:\:\:\:\:\:?? \\ $$
Commented by Penguin last updated on 07/Aug/20
Commented by Penguin last updated on 07/Aug/20
![Always makes triangle with A=(1/2)n(1−n) A=(1/n)(t_1 +t_2 +...t_n ) t_n =sum of nth triangle t_n =(1/2)n(1−n) t_(n+1) (1/2)(n+ε)(1−n−ε) for infinit triangles: A=(1/1)∫_0 ^( 1) (1/2)n(1−n)dn A=(1/2)[(1/2)n^2 −(1/3)n^3 ]_0 ^1 A=(1/(12)) Thks looks wrong, as the plot looks like: A=1−(π/4) ((1/4) circle in a sqare)](Q106877.png)
$$\mathrm{Always}\:\mathrm{makes}\:\mathrm{triangle}\:\mathrm{with}\:{A}=\frac{\mathrm{1}}{\mathrm{2}}{n}\left(\mathrm{1}−{n}\right) \\ $$$${A}=\frac{\mathrm{1}}{{n}}\left({t}_{\mathrm{1}} +{t}_{\mathrm{2}} +...{t}_{{n}} \right) \\ $$$${t}_{{n}} =\mathrm{sum}\:\mathrm{of}\:{n}\mathrm{th}\:\mathrm{triangle} \\ $$$$\: \\ $$$${t}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}{n}\left(\mathrm{1}−{n}\right) \\ $$$${t}_{{n}+\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}\left({n}+\varepsilon\right)\left(\mathrm{1}−{n}−\varepsilon\right) \\ $$$$\: \\ $$$$\mathrm{for}\:\mathrm{infinit}\:\mathrm{triangles}: \\ $$$${A}=\frac{\mathrm{1}}{\mathrm{1}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}{n}\left(\mathrm{1}−{n}\right){dn} \\ $$$${A}=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{1}}{\mathrm{2}}{n}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{3}}{n}^{\mathrm{3}} \right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$${A}=\frac{\mathrm{1}}{\mathrm{12}} \\ $$$$\mathrm{Thks}\:\mathrm{looks}\:\mathrm{wrong},\:\mathrm{as}\:\mathrm{the}\:\mathrm{plot}\:\mathrm{looks}\:\mathrm{like}: \\ $$$${A}=\mathrm{1}−\frac{\pi}{\mathrm{4}}\:\:\:\:\left(\frac{\mathrm{1}}{\mathrm{4}}\:\mathrm{circle}\:\mathrm{in}\:\mathrm{a}\:\mathrm{sqare}\right) \\ $$
Answered by Her_Majesty last updated on 07/Aug/20
![f_p : y=(p/(p−1))x+p f_q : y=(q/(q−1))x+q f_p ∩f_q : (p/(p−1))x+p=(q/(q−1))x+q x=(p−1)(q−1) y=pq now q→p x=(p−1)^2 y=p^2 p=1±(√x) y=(1±(√x))^2 =1±2(√x)+x your curve y=1−2(√x)+x ∫_0 ^1 (1−2(√x)+x)dx=[x−(4/3)x^(3/2) +(1/2)x^2 ]_0 ^1 =(1/6) not sure if this makes sense...](Q106915.png)
$${f}_{{p}} :\:{y}=\frac{{p}}{{p}−\mathrm{1}}{x}+{p} \\ $$$${f}_{{q}} :\:{y}=\frac{{q}}{{q}−\mathrm{1}}{x}+{q} \\ $$$${f}_{{p}} \cap{f}_{{q}} : \\ $$$$\frac{{p}}{{p}−\mathrm{1}}{x}+{p}=\frac{{q}}{{q}−\mathrm{1}}{x}+{q} \\ $$$${x}=\left({p}−\mathrm{1}\right)\left({q}−\mathrm{1}\right) \\ $$$${y}={pq} \\ $$$${now}\:{q}\rightarrow{p} \\ $$$${x}=\left({p}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$${y}={p}^{\mathrm{2}} \\ $$$${p}=\mathrm{1}\pm\sqrt{{x}} \\ $$$${y}=\left(\mathrm{1}\pm\sqrt{{x}}\right)^{\mathrm{2}} =\mathrm{1}\pm\mathrm{2}\sqrt{{x}}+{x} \\ $$$${your}\:{curve}\:{y}=\mathrm{1}−\mathrm{2}\sqrt{{x}}+{x} \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\left(\mathrm{1}−\mathrm{2}\sqrt{{x}}+{x}\right){dx}=\left[{x}−\frac{\mathrm{4}}{\mathrm{3}}{x}^{\mathrm{3}/\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} \right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{6}} \\ $$$${not}\:{sure}\:{if}\:{this}\:{makes}\:{sense}... \\ $$
Commented by mr W last updated on 07/Aug/20
$${answer}\:{is}\:{correct}! \\ $$
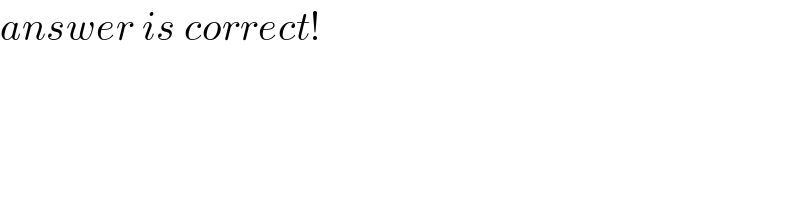
Answered by mr W last updated on 07/Aug/20
$$\frac{{y}}{{n}}+\frac{{x}}{\mathrm{1}−{n}}=\mathrm{1}\:\:\:...\left({i}\right)\:{eqn}.\:{of}\:{L}_{\mathrm{1}} \\ $$$$\frac{{y}}{{n}+{dn}}+\frac{{x}}{\mathrm{1}−{n}−{dn}}=\mathrm{1}\:\:\:...\left({ii}\right)\:{eqn}.\:{of}\:{L}_{\mathrm{2}} \\ $$$${intersection}\:{of}\:\left({i}\right)\:{and}\:\left({ii}\right)\:{at}\:\left({x}_{\mathrm{1}} ,{y}_{\mathrm{1}} \right) \\ $$$$\Rightarrow\frac{{y}_{\mathrm{1}} }{{n}\left(\mathrm{1}−{n}−{dn}\right)}−\frac{{y}_{\mathrm{1}} }{\left({n}+{dn}\right)\left(\mathrm{1}−{n}\right)}=\frac{\mathrm{1}}{\mathrm{1}−{n}−{dn}}−\frac{\mathrm{1}}{\mathrm{1}−{n}} \\ $$$$\Rightarrow{y}_{\mathrm{1}} ={n}\left({n}+{dn}\right) \\ $$$${dA}=\frac{{y}_{\mathrm{1}} {dn}}{\mathrm{2}}=\frac{{n}\left({n}+{dn}\right){dn}}{\mathrm{2}}=\frac{{n}^{\mathrm{2}} {dn}}{\mathrm{2}} \\ $$$${A}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{1}} {n}^{\mathrm{2}} {dn}=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{6}} \\ $$
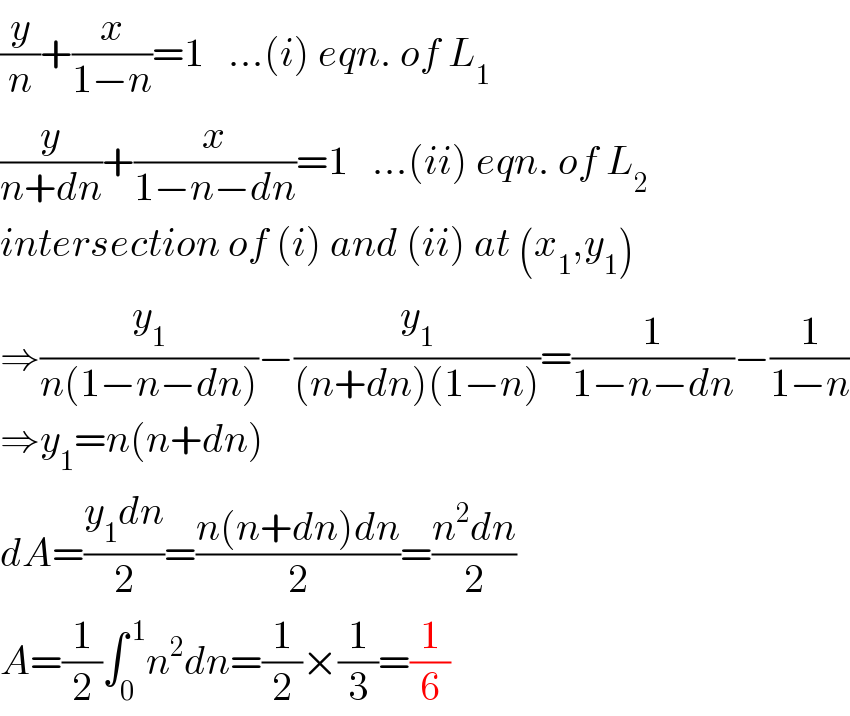
Commented by Her_Majesty last updated on 07/Aug/20
$${thank}\:{you} \\ $$
Commented by mr W last updated on 07/Aug/20
