Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 106948 by abdomathmax last updated on 08/Aug/20

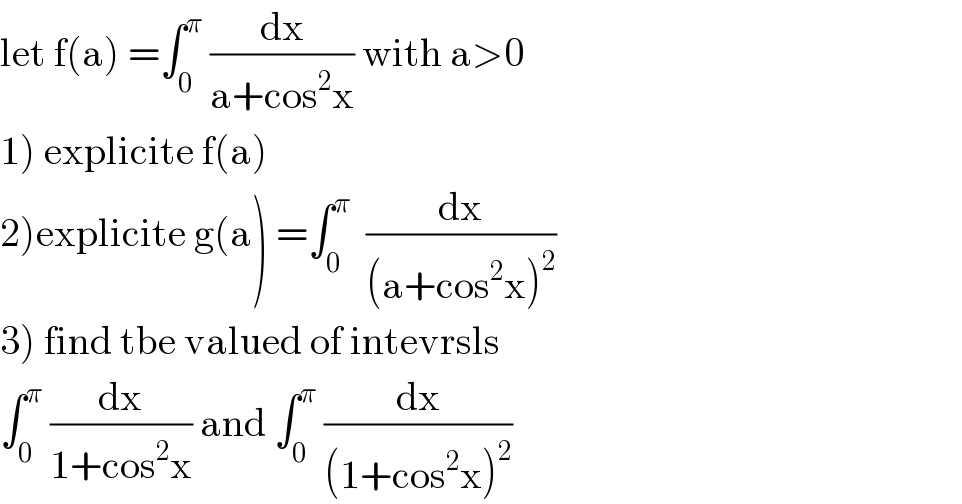
let f(a) =∫_0 ^π (dx/(a+cos^2 x)) with a>0 1) explicite f(a) 2)explicite g(a) =∫_0 ^π (dx/((a+cos^2 x)^2 )) 3) find tbe valued of intevrsls ∫_0 ^π (dx/(1+cos^2 x)) and ∫_0 ^π (dx/((1+cos^2 x)^2 ))

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{dx}}{\mathrm{a}+\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\:\mathrm{with}\:\mathrm{a}>\mathrm{0} \\ $$ $$\left.\mathrm{1}\right)\:\mathrm{explicite}\:\mathrm{f}\left(\mathrm{a}\right) \\ $$ $$\left.\mathrm{2}\right)\mathrm{explicite}\:\mathrm{g}\left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\pi} \:\:\frac{\mathrm{dx}}{\left(\mathrm{a}+\mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)^{\mathrm{2}} } \\ $$ $$\left.\mathrm{3}\right)\:\mathrm{find}\:\mathrm{tbe}\:\mathrm{valued}\:\mathrm{of}\:\mathrm{intevrsls} \\ $$ $$\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\:\mathrm{and}\:\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{dx}}{\left(\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)^{\mathrm{2}} } \\ $$

Answered by Ar Brandon last updated on 08/Aug/20

f(a)=∫_0 ^π (dx/(a+cos^2 x))=∫_0 ^π ((sec^2 x)/(asec^2 x+1))dx=∫_0 ^π ((d(tanx))/(a(1+tan^2 x)+1)) =∫_0 ^π ((d(tanx))/((a+1)+atan^2 x))=(1/a)∫_0 ^π ((d(tanx))/((((a+1)/a))+tan^2 x)) =(1/a)∙(√(a/(a+1)))[Arctan((√(a/(a+1)))∙tanx)]_0 ^π =(π/a)∙(√(a/(a+1)))=(π/(√(a^2 +a)))

$$\mathrm{f}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{dx}}{\mathrm{a}+\mathrm{cos}^{\mathrm{2}} \mathrm{x}}=\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{sec}^{\mathrm{2}} \mathrm{x}}{\mathrm{asec}^{\mathrm{2}} \mathrm{x}+\mathrm{1}}\mathrm{dx}=\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{d}\left(\mathrm{tanx}\right)}{\mathrm{a}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}\right)+\mathrm{1}} \\ $$ $$\:\:\:\:\:\:\:\:\:=\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{d}\left(\mathrm{tanx}\right)}{\left(\mathrm{a}+\mathrm{1}\right)+\mathrm{atan}^{\mathrm{2}} \mathrm{x}}=\frac{\mathrm{1}}{\mathrm{a}}\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{d}\left(\mathrm{tanx}\right)}{\left(\frac{\mathrm{a}+\mathrm{1}}{\mathrm{a}}\right)+\mathrm{tan}^{\mathrm{2}} \mathrm{x}} \\ $$ $$\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{a}}\centerdot\sqrt{\frac{\mathrm{a}}{\mathrm{a}+\mathrm{1}}}\left[\mathrm{Arctan}\left(\sqrt{\frac{\mathrm{a}}{\mathrm{a}+\mathrm{1}}}\centerdot\mathrm{tanx}\right)\right]_{\mathrm{0}} ^{\pi} \\ $$ $$\:\:\:\:\:\:\:\:\:=\frac{\pi}{\mathrm{a}}\centerdot\sqrt{\frac{\mathrm{a}}{\mathrm{a}+\mathrm{1}}}=\frac{\pi}{\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{a}}} \\ $$

Answered by Ar Brandon last updated on 08/Aug/20

g(a)=∫_0 ^π (dx/((a+cos^2 x)^2 ))=∫_0 ^π ((sec^4 x)/((asec^2 x+1)^2 ))dx =∫_0 ^π ((sec^2 x∙d(tanx))/((a+atan^2 x+1)^2 ))=∫_0 ^π ((1+tan^2 x)/((a+1+atan^2 x)^2 ))d(tanx) =∫_0 ^(−0) ((1+t^2 )/((a+1+at^2 )^2 ))dt=∫_0 ^(−0) ((1+t^2 )/((a+1)^2 +2a(a+1)+a^2 t^4 ))dt =(1/(2a))∫_0 ^(−0) (((a+1+at^2 )−(a+1−at^2 ))/((a+1)^2 +2a(a+1)+a^2 t^4 ))dt+∫_0 ^(−0) (1/((a+1)^2 +2a(a+1)+a^2 t^4 ))dt =(1/(2a)){∫_0 ^(−0) (((a+1)+at^2 )/((a+1)^2 +2a(a+1)+a^2 t^4 ))dt −∫_0 ^(−0) (((a+1)−at^2 )/((a+1)^2 +2a(a+1)+a^2 t^4 ))dt {: (),() }+I =(1/(2a)){∫_0 ^(−0) ((1+((a+1)/(at^2 )))/((((a+1)/(at)))^2 +((2(a+1))/t^2 )+at^2 ))+∫_0 ^(−0) ((1−((a+1)/(at^2 )))/((((a+1)/(at)))^2 +((2(a+1))/t^2 )+at^2 ))dt}+I ...

$$\mathrm{g}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{dx}}{\left(\mathrm{a}+\mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)^{\mathrm{2}} }=\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{sec}^{\mathrm{4}} \mathrm{x}}{\left(\mathrm{asec}^{\mathrm{2}} \mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$ $$\:\:\:\:\:\:\:\:\:\:=\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{sec}^{\mathrm{2}} \mathrm{x}\centerdot\mathrm{d}\left(\mathrm{tanx}\right)}{\left(\mathrm{a}+\mathrm{atan}^{\mathrm{2}} \mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }=\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}}{\left(\mathrm{a}+\mathrm{1}+\mathrm{atan}^{\mathrm{2}} \mathrm{x}\right)^{\mathrm{2}} }\mathrm{d}\left(\mathrm{tanx}\right) \\ $$ $$\:\:\:\:\:\:\:\:\:\:=\int_{\mathrm{0}} ^{−\mathrm{0}} \frac{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }{\left(\mathrm{a}+\mathrm{1}+\mathrm{at}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dt}=\int_{\mathrm{0}} ^{−\mathrm{0}} \frac{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }{\left(\mathrm{a}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{2a}\left(\mathrm{a}+\mathrm{1}\right)+\mathrm{a}^{\mathrm{2}} \mathrm{t}^{\mathrm{4}} }\mathrm{dt} \\ $$ $$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2a}}\int_{\mathrm{0}} ^{−\mathrm{0}} \frac{\left(\mathrm{a}+\mathrm{1}+\mathrm{at}^{\mathrm{2}} \right)−\left(\mathrm{a}+\mathrm{1}−\mathrm{at}^{\mathrm{2}} \right)}{\left(\mathrm{a}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{2a}\left(\mathrm{a}+\mathrm{1}\right)+\mathrm{a}^{\mathrm{2}} \mathrm{t}^{\mathrm{4}} }\mathrm{dt}+\int_{\mathrm{0}} ^{−\mathrm{0}} \frac{\mathrm{1}}{\left(\mathrm{a}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{2a}\left(\mathrm{a}+\mathrm{1}\right)+\mathrm{a}^{\mathrm{2}} \mathrm{t}^{\mathrm{4}} }\mathrm{dt} \\ $$ $$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2a}}\left\{\int_{\mathrm{0}} ^{−\mathrm{0}} \frac{\left(\mathrm{a}+\mathrm{1}\right)+\mathrm{at}^{\mathrm{2}} }{\left(\mathrm{a}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{2a}\left(\mathrm{a}+\mathrm{1}\right)+\mathrm{a}^{\mathrm{2}} \mathrm{t}^{\mathrm{4}} }\mathrm{dt}\right. \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\int_{\mathrm{0}} ^{−\mathrm{0}} \frac{\left(\mathrm{a}+\mathrm{1}\right)−\mathrm{at}^{\mathrm{2}} }{\left(\mathrm{a}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{2a}\left(\mathrm{a}+\mathrm{1}\right)+\mathrm{a}^{\mathrm{2}} \mathrm{t}^{\mathrm{4}} }\mathrm{dt\left.\begin{matrix}{}\\{}\end{matrix}\right\}}+\mathcal{I} \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2a}}\left\{\int_{\mathrm{0}} ^{−\mathrm{0}} \frac{\mathrm{1}+\frac{\mathrm{a}+\mathrm{1}}{\mathrm{at}^{\mathrm{2}} }}{\left(\frac{\mathrm{a}+\mathrm{1}}{\mathrm{at}}\right)^{\mathrm{2}} +\frac{\mathrm{2}\left(\mathrm{a}+\mathrm{1}\right)}{\mathrm{t}^{\mathrm{2}} }+\mathrm{at}^{\mathrm{2}} }+\int_{\mathrm{0}} ^{−\mathrm{0}} \frac{\mathrm{1}−\frac{\mathrm{a}+\mathrm{1}}{\mathrm{at}^{\mathrm{2}} }}{\left(\frac{\mathrm{a}+\mathrm{1}}{\mathrm{at}}\right)^{\mathrm{2}} +\frac{\mathrm{2}\left(\mathrm{a}+\mathrm{1}\right)}{\mathrm{t}^{\mathrm{2}} }+\mathrm{at}^{\mathrm{2}} }\mathrm{dt}\right\}+\mathcal{I} \\ $$ $$... \\ $$

Answered by Ar Brandon last updated on 08/Aug/20

f(1)=∫_0 ^π (dx/(1+cos^2 x))=(π/(√(1^2 +1)))=(π/(√2)) g(1)=∫_0 ^π (dx/((1+cos^2 x)^2 ))=∫_0 ^π ((sec^4 x)/((sec^2 x+1)^2 ))dx =∫_0 ^π ((1+tan^2 x)/((2+tan^2 x)^2 ))d(tanx)=∫_0 ^(−0) ((1+t^2 )/((2+t^2 )^2 ))dt =∫_0 ^(−0) ((2+t^2 )/((2+t^2 )^2 ))dt−∫_0 ^(−0) (1/((2+t^2 )^2 ))dt =_(t=(√2)tanθ) ∫_0 ^(−0) (dt/(2+t^2 ))−(1/4)∫_0 ^π (((√2)sec^2 θdθ)/((1+tan^2 θ)^2 )) =[(1/(√2))Arctan((t/(√2)))]_0 ^(−0) −((√2)/4)∫_0 ^π (dθ/(sec^2 θ)) =(π/(√2))−((√2)/4)∙(1/2)∫_0 ^π (1+cos2θ)dθ=(π/(√2))−(1/(4(√2)))[θ+((sin2θ)/2)]_0 ^π =(π/(√2))−(π/(4(√2)))=((3π)/(4(√2)))

$$\mathrm{f}\left(\mathrm{1}\right)=\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{dx}}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \mathrm{x}}=\frac{\pi}{\sqrt{\mathrm{1}^{\mathrm{2}} +\mathrm{1}}}=\frac{\pi}{\sqrt{\mathrm{2}}} \\ $$ $$\mathrm{g}\left(\mathrm{1}\right)=\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{dx}}{\left(\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)^{\mathrm{2}} }=\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{sec}^{\mathrm{4}} \mathrm{x}}{\left(\mathrm{sec}^{\mathrm{2}} \mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$ $$\:\:\:\:\:\:\:\:\:=\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}}{\left(\mathrm{2}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}\right)^{\mathrm{2}} }\mathrm{d}\left(\mathrm{tanx}\right)=\int_{\mathrm{0}} ^{−\mathrm{0}} \frac{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }{\left(\mathrm{2}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dt} \\ $$ $$\:\:\:\:\:\:\:\:\:=\int_{\mathrm{0}} ^{−\mathrm{0}} \frac{\mathrm{2}+\mathrm{t}^{\mathrm{2}} }{\left(\mathrm{2}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dt}−\int_{\mathrm{0}} ^{−\mathrm{0}} \frac{\mathrm{1}}{\left(\mathrm{2}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dt} \\ $$ $$\:\:\:\underset{\mathrm{t}=\sqrt{\mathrm{2}}\mathrm{tan}\theta} {=}\int_{\mathrm{0}} ^{−\mathrm{0}} \frac{\mathrm{dt}}{\mathrm{2}+\mathrm{t}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\pi} \frac{\sqrt{\mathrm{2}}\mathrm{sec}^{\mathrm{2}} \theta\mathrm{d}\theta}{\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta\right)^{\mathrm{2}} } \\ $$ $$\:\:\:\:\:\:\:\:=\left[\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\mathrm{Arctan}\left(\frac{\mathrm{t}}{\sqrt{\mathrm{2}}}\right)\right]_{\mathrm{0}} ^{−\mathrm{0}} −\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{d}\theta}{\mathrm{sec}^{\mathrm{2}} \theta} \\ $$ $$\:\:\:\:\:\:\:\:=\frac{\pi}{\sqrt{\mathrm{2}}}−\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\centerdot\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\pi} \left(\mathrm{1}+\mathrm{cos2}\theta\right)\mathrm{d}\theta=\frac{\pi}{\sqrt{\mathrm{2}}}−\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\left[\theta+\frac{\mathrm{sin2}\theta}{\mathrm{2}}\right]_{\mathrm{0}} ^{\pi} \\ $$ $$\:\:\:\:\:\:\:\:=\frac{\pi}{\sqrt{\mathrm{2}}}−\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}}=\frac{\mathrm{3}\pi}{\mathrm{4}\sqrt{\mathrm{2}}} \\ $$

Commented byAr Brandon last updated on 08/Aug/20

You're welcome, senior.��

Commented byabdomathmax last updated on 08/Aug/20

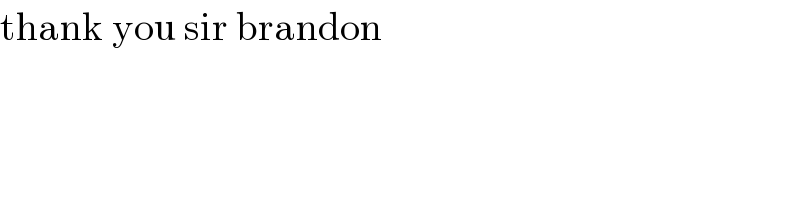
thank you sir brandon

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}\:\mathrm{brandon} \\ $$

Answered by mathmax by abdo last updated on 08/Aug/20

1) residus method f(a) =∫_0 ^π (dx/(a+cos^2 x)) ⇒f(a) =∫_0 ^π (dx/(a+((1+cos(2x))/2))) =2 ∫_0 ^π (dx/(2a+1+cos(2x))) =_(2x=t) 2 ∫_0 ^(2π) (dt/(2(2a+1+cost))) =∫_0 ^(2π) (dt/(2a+1+cost)) =_(e^(it) =z) ∫_(∣z∣=1) (dz/(iz(2a+1+((z+z^(−1) )/2)))) =∫ ((−2idz)/(z(4a+2+z+z^(−1) ))) =∫ ((−2idz)/((4a+2)z +z^2 +1)) let ϕ(z) =((−2i)/(z^2 +(4a+2)z +1)) poles of ϕ? Δ^′ =(2a+1)^2 −1 =4a^2 +4a+1−1 =4a^2 +4a ⇒ z_1 =−(2a+1)+2(√(a^2 +a)) and z_2 =−(2a+1)−2(√(a^2 +a)) ∣z_1 ∣ −1 =∣2(√(a^2 +a))−(2a+1)∣−1 =2a+1−2(√(a^2 +a))−1 =2a−2(√(a^2 +a))=2(a−(√(a^2 +a)))<0 ⇒∣z_1 ∣<1 ∣z_2 ∣−1 =2a+1+2(√(a^2 +a))−1 >0 ⇒∣z_2 ∣>1(to eliminate from residus) ⇒ ∫_(∣z∣=1) ϕ(2)dz =2iπ Res(ϕ,z_1 ) =2iπ×((−2i)/(z_1 −z_2 )) =((4π)/(4(√(a^2 +a)))) =(π/(√(a^2 +a))) ⇒f(a) =(π/(√(a^2 +a))) (a>0) 2)we have f^′ (a) =−∫_0 ^π (dx/((a+cos^2 x)^2 )) =−g(a) ⇒ g(a) =−f^′ (a) but f^′ (a) =−π ×((((√(a^2 +a)))^′ )/(a^2 +a⇒)) =−π×((2a+1)/(2(a^2 +a)(√(a^2 +a)))) ⇒g(a) =(((2a+1)π)/(2(a^2 +a)(√(a^2 +a)))) 3) ∫_0 ^π (dx/(1+cos^2 x)) =f(1) =(π/(√2)) ∫_0 ^π (dx/((1+cos^2 x)^2 )) =g(1) =((3π)/(4(√2)))

$$\left.\mathrm{1}\right)\:\mathrm{residus}\:\mathrm{method}\:\mathrm{f}\left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{dx}}{\mathrm{a}+\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\:\Rightarrow\mathrm{f}\left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{dx}}{\mathrm{a}+\frac{\mathrm{1}+\mathrm{cos}\left(\mathrm{2x}\right)}{\mathrm{2}}} \\ $$ $$=\mathrm{2}\:\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{dx}}{\mathrm{2a}+\mathrm{1}+\mathrm{cos}\left(\mathrm{2x}\right)}\:=_{\mathrm{2x}=\mathrm{t}} \:\:\:\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\frac{\mathrm{dt}}{\mathrm{2}\left(\mathrm{2a}+\mathrm{1}+\mathrm{cost}\right)}\:=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{\mathrm{dt}}{\mathrm{2a}+\mathrm{1}+\mathrm{cost}} \\ $$ $$=_{\mathrm{e}^{\mathrm{it}} \:=\mathrm{z}} \:\:\:\:\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\:\:\:\:\:\frac{\mathrm{dz}}{\mathrm{iz}\left(\mathrm{2a}+\mathrm{1}+\frac{\mathrm{z}+\mathrm{z}^{−\mathrm{1}} }{\mathrm{2}}\right)}\:=\int\:\frac{−\mathrm{2idz}}{\mathrm{z}\left(\mathrm{4a}+\mathrm{2}+\mathrm{z}+\mathrm{z}^{−\mathrm{1}} \right)} \\ $$ $$=\int\:\:\frac{−\mathrm{2idz}}{\left(\mathrm{4a}+\mathrm{2}\right)\mathrm{z}\:+\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}}\:\:\mathrm{let}\:\varphi\left(\mathrm{z}\right)\:=\frac{−\mathrm{2i}}{\mathrm{z}^{\mathrm{2}} \:+\left(\mathrm{4a}+\mathrm{2}\right)\mathrm{z}\:+\mathrm{1}}\:\:\mathrm{poles}\:\mathrm{of}\:\varphi? \\ $$ $$\Delta^{'} \:=\left(\mathrm{2a}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}\:=\mathrm{4a}^{\mathrm{2}} +\mathrm{4a}+\mathrm{1}−\mathrm{1}\:=\mathrm{4a}^{\mathrm{2}} \:+\mathrm{4a}\:\Rightarrow \\ $$ $$\mathrm{z}_{\mathrm{1}} =−\left(\mathrm{2a}+\mathrm{1}\right)+\mathrm{2}\sqrt{\mathrm{a}^{\mathrm{2}} \:+\mathrm{a}}\:\:\mathrm{and}\:\mathrm{z}_{\mathrm{2}} =−\left(\mathrm{2a}+\mathrm{1}\right)−\mathrm{2}\sqrt{\mathrm{a}^{\mathrm{2}} \:+\mathrm{a}} \\ $$ $$\mid\mathrm{z}_{\mathrm{1}} \mid\:−\mathrm{1}\:=\mid\mathrm{2}\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{a}}−\left(\mathrm{2a}+\mathrm{1}\right)\mid−\mathrm{1}\:=\mathrm{2a}+\mathrm{1}−\mathrm{2}\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{a}}−\mathrm{1} \\ $$ $$=\mathrm{2a}−\mathrm{2}\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{a}}=\mathrm{2}\left(\mathrm{a}−\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{a}}\right)<\mathrm{0}\:\Rightarrow\mid\mathrm{z}_{\mathrm{1}} \mid<\mathrm{1} \\ $$ $$\mid\mathrm{z}_{\mathrm{2}} \mid−\mathrm{1}\:=\mathrm{2a}+\mathrm{1}+\mathrm{2}\sqrt{\mathrm{a}^{\mathrm{2}} \:+\mathrm{a}}−\mathrm{1}\:>\mathrm{0}\:\Rightarrow\mid\mathrm{z}_{\mathrm{2}} \mid>\mathrm{1}\left(\mathrm{to}\:\mathrm{eliminate}\:\mathrm{from}\:\mathrm{residus}\right) \\ $$ $$\Rightarrow\:\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\:\varphi\left(\mathrm{2}\right)\mathrm{dz}\:=\mathrm{2i}\pi\:\mathrm{Res}\left(\varphi,\mathrm{z}_{\mathrm{1}} \right)\:=\mathrm{2i}\pi×\frac{−\mathrm{2i}}{\mathrm{z}_{\mathrm{1}} −\mathrm{z}_{\mathrm{2}} } \\ $$ $$=\frac{\mathrm{4}\pi}{\mathrm{4}\sqrt{\mathrm{a}^{\mathrm{2}} \:+\mathrm{a}}}\:=\frac{\pi}{\sqrt{\mathrm{a}^{\mathrm{2}} \:+\mathrm{a}}}\:\Rightarrow\mathrm{f}\left(\mathrm{a}\right)\:=\frac{\pi}{\sqrt{\mathrm{a}^{\mathrm{2}} \:+\mathrm{a}}}\:\:\:\left(\mathrm{a}>\mathrm{0}\right) \\ $$ $$\left.\mathrm{2}\right)\mathrm{we}\:\mathrm{have}\:\mathrm{f}^{'} \left(\mathrm{a}\right)\:=−\int_{\mathrm{0}} ^{\pi} \:\:\frac{\mathrm{dx}}{\left(\mathrm{a}+\mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)^{\mathrm{2}} }\:=−\mathrm{g}\left(\mathrm{a}\right)\:\Rightarrow \\ $$ $$\mathrm{g}\left(\mathrm{a}\right)\:=−\mathrm{f}^{'} \left(\mathrm{a}\right)\:\:\mathrm{but}\:\:\mathrm{f}^{'} \left(\mathrm{a}\right)\:=−\pi\:×\frac{\left(\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{a}}\right)^{'} }{\mathrm{a}^{\mathrm{2}} \:+\mathrm{a}\Rightarrow}\:=−\pi×\frac{\mathrm{2a}+\mathrm{1}}{\mathrm{2}\left(\mathrm{a}^{\mathrm{2}} \:+\mathrm{a}\right)\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{a}}} \\ $$ $$\Rightarrow\mathrm{g}\left(\mathrm{a}\right)\:=\frac{\left(\mathrm{2a}+\mathrm{1}\right)\pi}{\mathrm{2}\left(\mathrm{a}^{\mathrm{2}} \:+\mathrm{a}\right)\sqrt{\mathrm{a}^{\mathrm{2}} \:+\mathrm{a}}} \\ $$ $$\left.\mathrm{3}\right)\:\int_{\mathrm{0}} ^{\pi} \:\:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\:=\mathrm{f}\left(\mathrm{1}\right)\:=\frac{\pi}{\sqrt{\mathrm{2}}} \\ $$ $$\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{dx}}{\left(\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)^{\mathrm{2}} }\:=\mathrm{g}\left(\mathrm{1}\right)\:=\frac{\mathrm{3}\pi}{\mathrm{4}\sqrt{\mathrm{2}}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com