Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 106964 by Ar Brandon last updated on 08/Aug/20

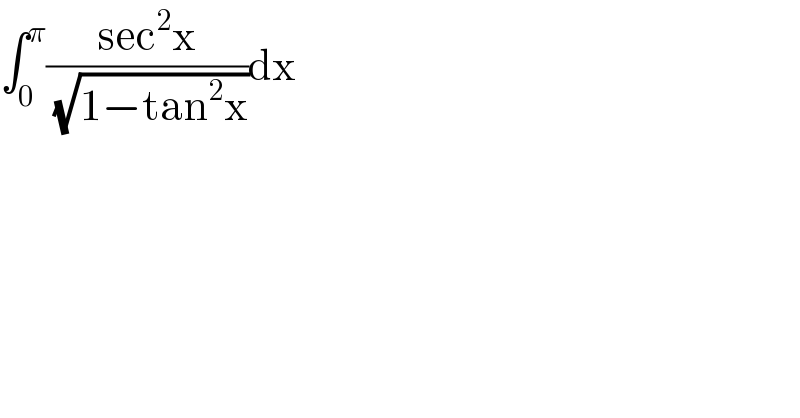
∫_0 ^π ((sec^2 x)/(√(1−tan^2 x)))dx

$$\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{sec}^{\mathrm{2}} \mathrm{x}}{\sqrt{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \mathrm{x}}}\mathrm{dx} \\ $$

Commented by Her_Majesty last updated on 08/Aug/20

I believe this integral is divergent must sleep now to keep my majestic beauty will try to show later

$${I}\:{believe}\:{this}\:{integral}\:{is}\:{divergent} \\ $$$${must}\:{sleep}\:{now}\:{to}\:{keep}\:{my}\:{majestic}\:{beauty} \\ $$$${will}\:{try}\:{to}\:{show}\:{later} \\ $$

Commented by Dwaipayan Shikari last updated on 08/Aug/20

probably

$$\mathrm{probably} \\ $$

Commented by Dwaipayan Shikari last updated on 08/Aug/20

Commented by Ar Brandon last updated on 08/Aug/20

��Alright her majesty ��

Answered by bemath last updated on 08/Aug/20

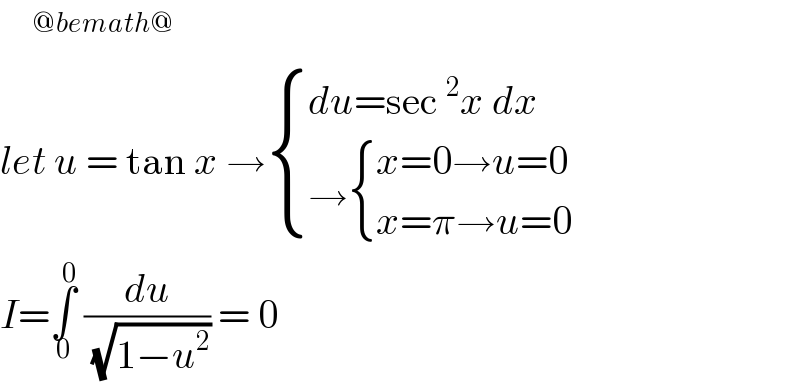
^(@bemath@) let u = tan x → { ((du=sec^2 x dx)),((→ { ((x=0→u=0)),((x=π→u=0)) :})) :} I=∫_0 ^0 (du/(√(1−u^2 ))) = 0

$$\:\:\:\:^{@{bemath}@} \\ $$$${let}\:{u}\:=\:\mathrm{tan}\:{x}\:\rightarrow\begin{cases}{{du}=\mathrm{sec}\:^{\mathrm{2}} {x}\:{dx}}\\{\rightarrow\begin{cases}{{x}=\mathrm{0}\rightarrow{u}=\mathrm{0}}\\{{x}=\pi\rightarrow{u}=\mathrm{0}}\end{cases}}\end{cases} \\ $$$${I}=\underset{\mathrm{0}} {\overset{\mathrm{0}} {\int}}\:\frac{{du}}{\sqrt{\mathrm{1}−{u}^{\mathrm{2}} }}\:=\:\mathrm{0} \\ $$

Answered by 1549442205PVT last updated on 08/Aug/20

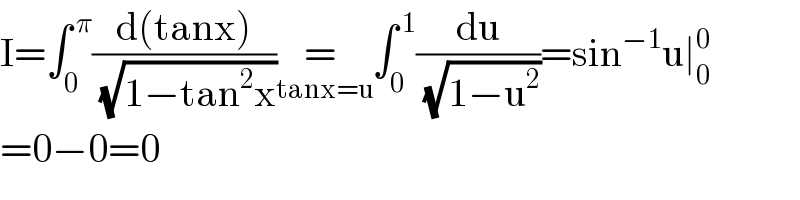
I=∫_0 ^( π) ((d(tanx))/(√(1−tan^2 x)))= _(tanx=u) ∫_0 ^( 1) (du/(√(1−u^2 )))=sin^(−1) u∣_0 ^0 =0−0=0

$$\mathrm{I}=\int_{\mathrm{0}} ^{\:\pi} \frac{\mathrm{d}\left(\mathrm{tanx}\right)}{\sqrt{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \mathrm{x}}}\underset{\mathrm{tanx}=\mathrm{u}} {=\:}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{du}}{\sqrt{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }}=\mathrm{sin}^{−\mathrm{1}} \mathrm{u}\mid_{\mathrm{0}} ^{\mathrm{0}} \\ $$$$=\mathrm{0}−\mathrm{0}=\mathrm{0} \\ $$

Answered by Dwaipayan Shikari last updated on 08/Aug/20

∫_0 ^π (dt/(√(1−t^2 ))) tanx=t ,sec^2 x=(dt/dx) [sin^(−1) (tanx)]_0 ^π =0

$$\int_{\mathrm{0}} ^{\pi} \frac{{dt}}{\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}\:\:\:\:\:\:\:\:\:\:{tanx}={t}\:\:\:\:\:,{sec}^{\mathrm{2}} {x}=\frac{{dt}}{{dx}} \\ $$$$\left[{sin}^{−\mathrm{1}} \left({tanx}\right)\right]_{\mathrm{0}} ^{\pi} =\mathrm{0} \\ $$

Commented by Ar Brandon last updated on 08/Aug/20

Thank y′all. I really needed to verify something. And you′ve been of great help.

$$\mathrm{Thank}\:\mathrm{y}'\mathrm{all}.\:\mathrm{I}\:\mathrm{really}\:\mathrm{needed}\:\mathrm{to}\:\mathrm{verify}\:\mathrm{something}. \\ $$$$\mathrm{And}\:\mathrm{you}'\mathrm{ve}\:\mathrm{been}\:\mathrm{of}\:\mathrm{great}\:\mathrm{help}. \\ $$

Answered by Ar Brandon last updated on 08/Aug/20

I=∫_0 ^(π/2) ((sec^2 x)/(√(1−tan^2 x)))dx+∫_(π/2) ^π ((sec^2 x)/(√(1−tan^2 x)))dx =∫_0 ^(π/2) ((sec^2 x)/(√(1−tan^2 x)))dx−∫_0 ^(π/2) ((sec^2 x)/(√(1−tan^2 x)))dx=0

$$\mathcal{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sec}^{\mathrm{2}} \mathrm{x}}{\sqrt{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \mathrm{x}}}\mathrm{dx}+\int_{\frac{\pi}{\mathrm{2}}} ^{\pi} \frac{\mathrm{sec}^{\mathrm{2}} \mathrm{x}}{\sqrt{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \mathrm{x}}}\mathrm{dx} \\ $$$$\:\:\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sec}^{\mathrm{2}} \mathrm{x}}{\sqrt{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \mathrm{x}}}\mathrm{dx}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sec}^{\mathrm{2}} \mathrm{x}}{\sqrt{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \mathrm{x}}}\mathrm{dx}=\mathrm{0} \\ $$

Answered by Her_Majesty last updated on 08/Aug/20

y=((sec^2 x)/(√(1−tan^2 x)))=(1/(∣cosx∣(√(cos2x)))) for 0≤x≤π y is defined for 0≤x<(π/4) and ((3π)/4)<y≤π ⇒ the integral only exists if the imaginary/complex parts cancel out but let′s try ∫_0 ^π (dx/(∣cosx∣(√(cos2x))))=2∫_0 ^(π/2) (dx/(cosx(√(cos2x)))) with t=tanx we get ∫_0 ^(π/2) (dx/(cosx(√(cos2x))))=∫_0 ^(+∞) (dt/(√(1−t^2 )))=[arcsin(t)]_0 ^(+∞) = =lim_(t→+∞) arcsin(t) which is (π/2)−i∞ (try some values like t=10^(10) , 10^(20) ... ⇒ the integral is divergent

$${y}=\frac{{sec}^{\mathrm{2}} {x}}{\sqrt{\mathrm{1}−{tan}^{\mathrm{2}} {x}}}=\frac{\mathrm{1}}{\mid{cosx}\mid\sqrt{{cos}\mathrm{2}{x}}} \\ $$$${for}\:\mathrm{0}\leqslant{x}\leqslant\pi\:\:{y}\:{is}\:{defined}\:{for}\:\mathrm{0}\leqslant{x}<\frac{\pi}{\mathrm{4}}\:{and} \\ $$$$\frac{\mathrm{3}\pi}{\mathrm{4}}<{y}\leqslant\pi\:\:\Rightarrow\:{the}\:{integral}\:{only}\:{exists}\:{if}\:{the} \\ $$$${imaginary}/{complex}\:{parts}\:{cancel}\:{out} \\ $$$${but}\:{let}'{s}\:{try} \\ $$$$\underset{\mathrm{0}} {\overset{\pi} {\int}}\frac{{dx}}{\mid{cosx}\mid\sqrt{{cos}\mathrm{2}{x}}}=\mathrm{2}\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\frac{{dx}}{{cosx}\sqrt{{cos}\mathrm{2}{x}}} \\ $$$${with}\:{t}={tanx}\:{we}\:{get} \\ $$$$\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\frac{{dx}}{{cosx}\sqrt{{cos}\mathrm{2}{x}}}=\underset{\mathrm{0}} {\overset{+\infty} {\int}}\frac{{dt}}{\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}=\left[{arcsin}\left({t}\right)\right]_{\mathrm{0}} ^{+\infty} = \\ $$$$=\underset{{t}\rightarrow+\infty} {{lim}arcsin}\left({t}\right)\:{which}\:{is}\:\frac{\pi}{\mathrm{2}}−{i}\infty\:\left({try}\:{some}\right. \\ $$$${values}\:{like}\:{t}=\mathrm{10}^{\mathrm{10}} ,\:\mathrm{10}^{\mathrm{20}} ... \\ $$$$\Rightarrow\:{the}\:{integral}\:{is}\:{divergent} \\ $$

Commented by Ar Brandon last updated on 08/Aug/20

OK Sir, thanks

Terms of Service

Privacy Policy

Contact: info@tinkutara.com