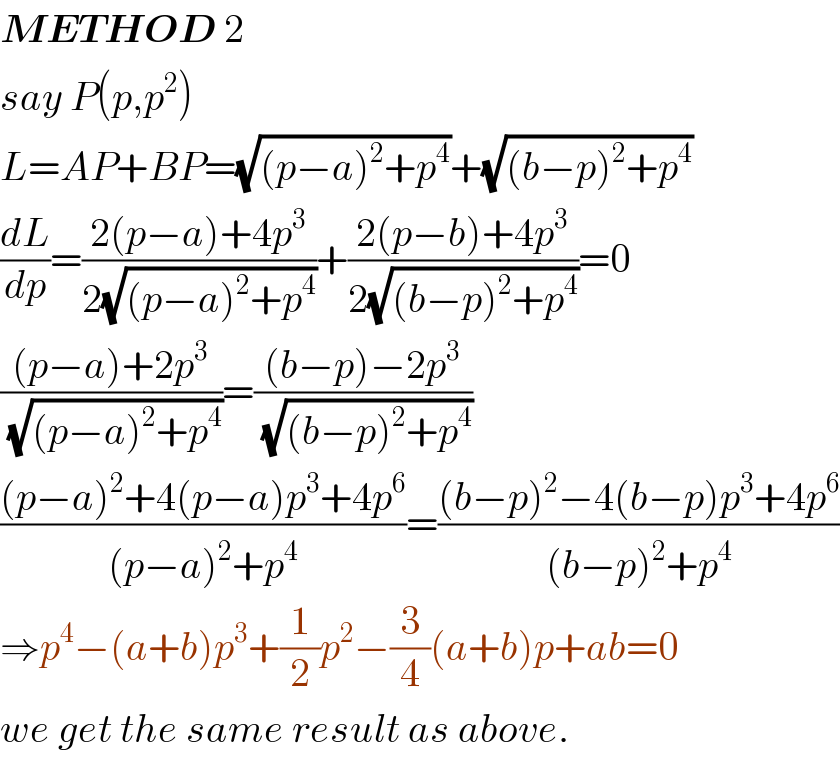Question and Answers Forum
Question Number 106977 by mr W last updated on 08/Aug/20
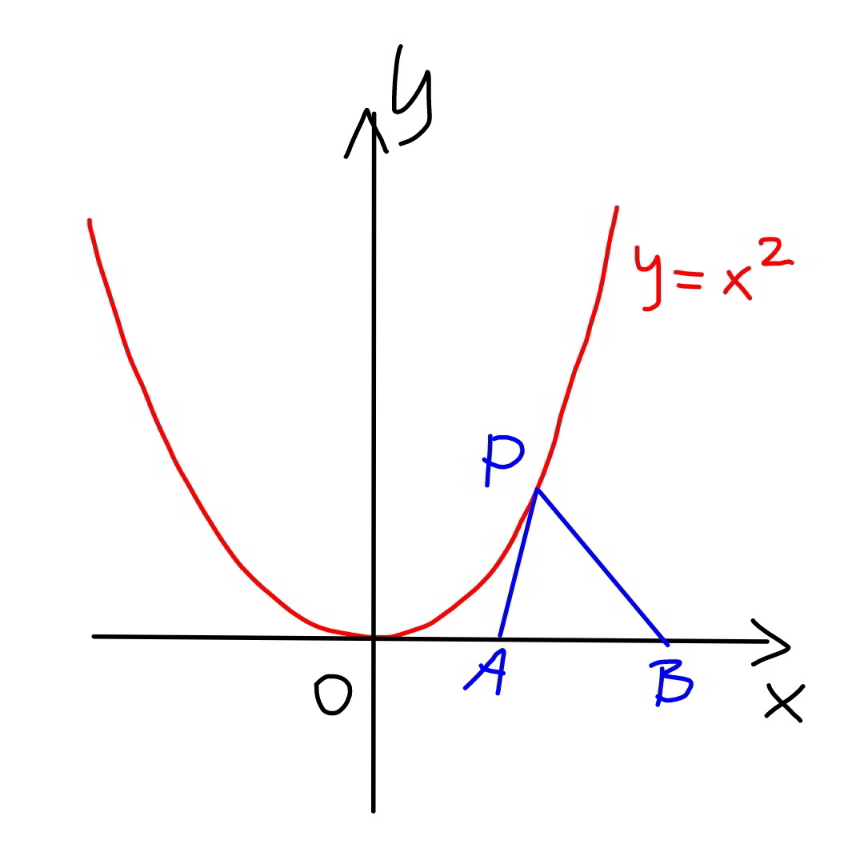
Answered by mr W last updated on 08/Aug/20

Commented by PRITHWISH SEN 2 last updated on 08/Aug/20

Answered by mr W last updated on 08/Aug/20
![METHOD I say P(p,p^2 ) tangent at P is y=p^2 +2p(x−p) ⇒2px−y−p^2 =0 image of B in tangent is C(x_C ,y_C ) x_C =b−((4p(2pb−p^2 ))/(4p^2 +1)) y_C =((2(2pb−p^2 ))/(4p^2 +1)) A,P,C are collinear, ((y_C −p^2 )/p^2 )=((x_C −p)/(p−a)) ((2(2pb−p^2 ))/(4p^2 +1))−p^2 =(p^2 /(p−a))[b−((4p(2pb−p^2 ))/(4p^2 +1))−p] ⇒p^4 −(a+b)p^3 +(1/2)p^2 −(3/4)(a+b)p+ab=0 ⇒p=....](Q107008.png)
Commented by PRITHWISH SEN 2 last updated on 08/Aug/20

Commented by mr W last updated on 08/Aug/20
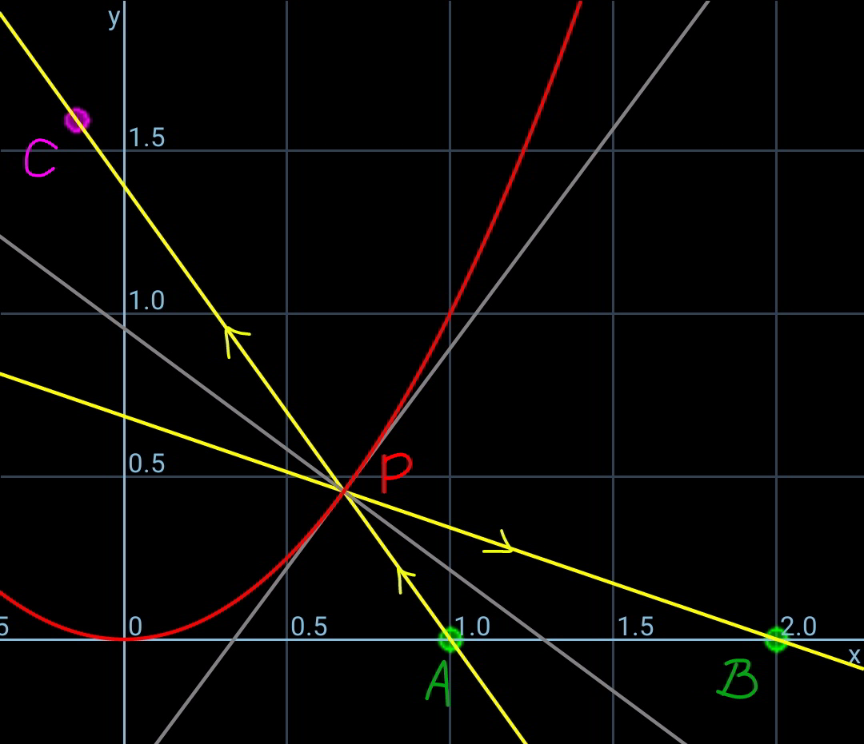
Commented by mr W last updated on 08/Aug/20

Commented by PRITHWISH SEN 2 last updated on 08/Aug/20

Commented by mr W last updated on 08/Aug/20

Commented by PRITHWISH SEN 2 last updated on 08/Aug/20
Commented by mr W last updated on 08/Aug/20

Commented by PRITHWISH SEN 2 last updated on 08/Aug/20

Answered by mr W last updated on 08/Aug/20