Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 107030 by bemath last updated on 08/Aug/20

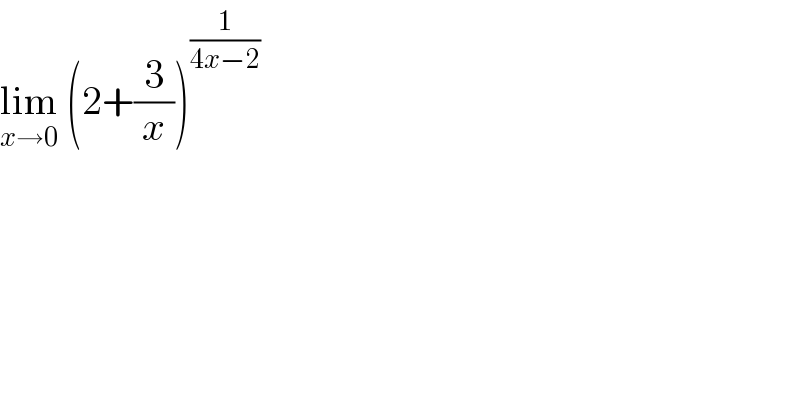
lim_(x→0) (2+(3/x))^(1/(4x−2))

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\mathrm{2}+\frac{\mathrm{3}}{{x}}\right)^{\frac{\mathrm{1}}{\mathrm{4}{x}−\mathrm{2}}} \\ $$

Commented by kaivan.ahmadi last updated on 08/Aug/20

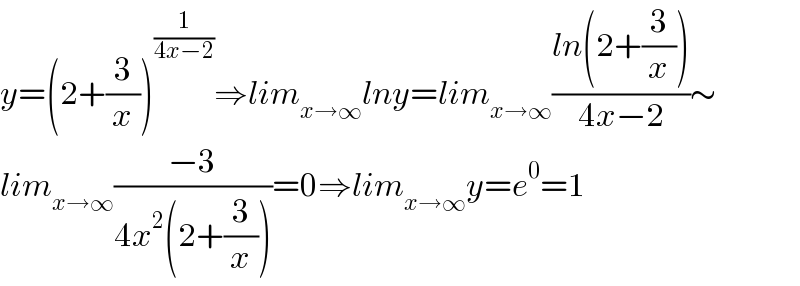
y=(2+(3/x))^(1/(4x−2)) ⇒lim_(x→∞) lny=lim_(x→∞) ((ln(2+(3/x)))/(4x−2))∼ lim_(x→∞) ((−3)/(4x^2 (2+(3/x))))=0⇒lim_(x→∞) y=e^0 =1

$${y}=\left(\mathrm{2}+\frac{\mathrm{3}}{{x}}\right)^{\frac{\mathrm{1}}{\mathrm{4}{x}−\mathrm{2}}} \Rightarrow{lim}_{{x}\rightarrow\infty} {lny}={lim}_{{x}\rightarrow\infty} \frac{{ln}\left(\mathrm{2}+\frac{\mathrm{3}}{{x}}\right)}{\mathrm{4}{x}−\mathrm{2}}\sim \\ $$$${lim}_{{x}\rightarrow\infty} \frac{−\mathrm{3}}{\mathrm{4}{x}^{\mathrm{2}} \left(\mathrm{2}+\frac{\mathrm{3}}{{x}}\right)}=\mathrm{0}\Rightarrow{lim}_{{x}\rightarrow\infty} {y}={e}^{\mathrm{0}} =\mathrm{1} \\ $$

Answered by Dwaipayan Shikari last updated on 08/Aug/20

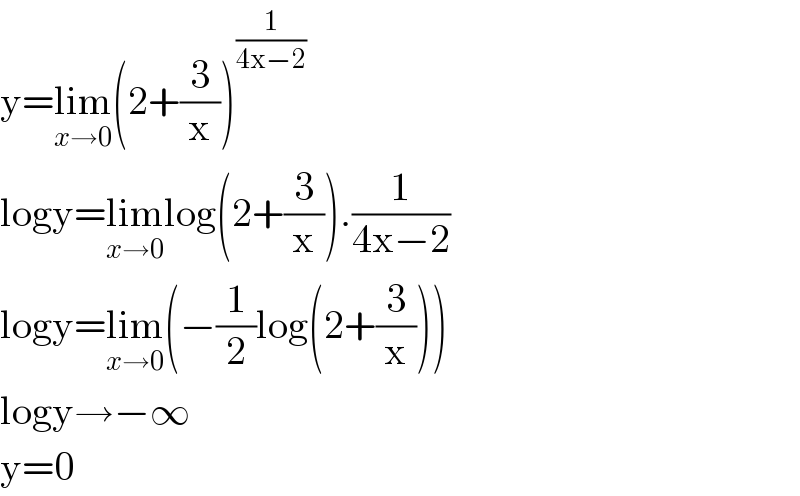
y=lim_(x→0) (2+(3/x))^(1/(4x−2)) logy=lim_(x→0) log(2+(3/x)).(1/(4x−2)) logy=lim_(x→0) (−(1/2)log(2+(3/x))) logy→−∞ y=0

$$\mathrm{y}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{2}+\frac{\mathrm{3}}{\mathrm{x}}\right)^{\frac{\mathrm{1}}{\mathrm{4x}−\mathrm{2}}} \\ $$$$\mathrm{logy}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}log}\left(\mathrm{2}+\frac{\mathrm{3}}{\mathrm{x}}\right).\frac{\mathrm{1}}{\mathrm{4x}−\mathrm{2}} \\ $$$$\mathrm{logy}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\left(\mathrm{2}+\frac{\mathrm{3}}{\mathrm{x}}\right)\right) \\ $$$$\mathrm{logy}\rightarrow−\infty \\ $$$$\mathrm{y}=\mathrm{0} \\ $$

Commented by bemath last updated on 08/Aug/20

not correct sir

$${not}\:{correct}\:{sir} \\ $$

Commented by Dwaipayan Shikari last updated on 08/Aug/20

Commented by bemath last updated on 08/Aug/20

Answered by john santu last updated on 08/Aug/20

@JS@ we have formula lim_(x→0) (1+x)^(1/x) = e lim_(x→0) (1+(((x+3)/x)))^(1/(4x−2)) = lim_(x→0) [(1+(((x+3)/x)))^(((x/(x+3)))) ]^((x+3)/(x(4x−2))) = e^(lim_(x→0 ) (((x+3)/(4x^2 −2x)))) = e^∞ = ∞

$$\:\:\:\:\:\:@\mathrm{JS}@ \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{formula}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{1}+\mathrm{x}\right)^{\frac{\mathrm{1}}{\mathrm{x}}} =\:\mathrm{e} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{1}+\left(\frac{\mathrm{x}+\mathrm{3}}{\mathrm{x}}\right)\right)^{\frac{\mathrm{1}}{\mathrm{4x}−\mathrm{2}}} =\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\left(\mathrm{1}+\left(\frac{\mathrm{x}+\mathrm{3}}{\mathrm{x}}\right)\right)^{\left(\frac{\mathrm{x}}{\mathrm{x}+\mathrm{3}}\right)} \right]^{\frac{\mathrm{x}+\mathrm{3}}{\mathrm{x}\left(\mathrm{4x}−\mathrm{2}\right)}} \\ $$$$=\:\mathrm{e}\:^{\underset{{x}\rightarrow\mathrm{0}\:} {\mathrm{lim}}\left(\frac{\mathrm{x}+\mathrm{3}}{\mathrm{4x}^{\mathrm{2}} −\mathrm{2x}}\right)} =\:\mathrm{e}^{\infty} \:=\:\infty\: \\ $$

Commented by bemath last updated on 08/Aug/20

thank you

$${thank}\:{you} \\ $$

Answered by bemath last updated on 08/Aug/20

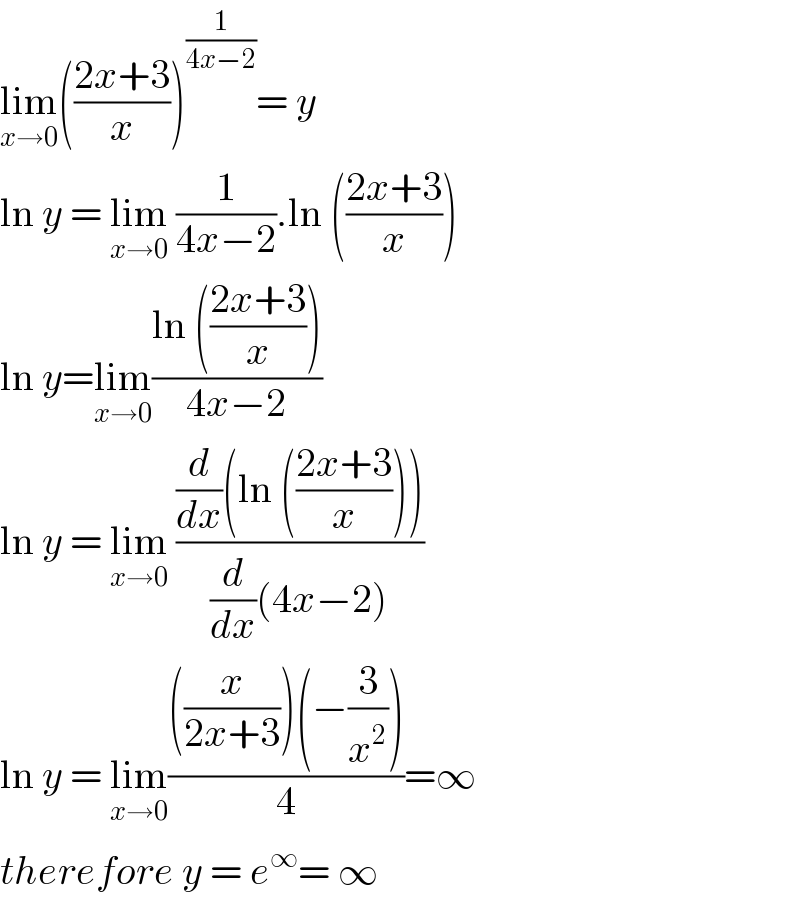
lim_(x→0) (((2x+3)/x))^(1/(4x−2)) = y ln y = lim_(x→0) (1/(4x−2)).ln (((2x+3)/x)) ln y=lim_(x→0) ((ln (((2x+3)/x)))/(4x−2)) ln y = lim_(x→0) (((d/dx)(ln (((2x+3)/x))))/((d/dx)(4x−2))) ln y = lim_(x→0) ((((x/(2x+3)))(−(3/x^2 )))/4)=∞ therefore y = e^∞ = ∞

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{2}{x}+\mathrm{3}}{{x}}\right)^{\frac{\mathrm{1}}{\mathrm{4}{x}−\mathrm{2}}} =\:{y} \\ $$$$\mathrm{ln}\:{y}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{4}{x}−\mathrm{2}}.\mathrm{ln}\:\left(\frac{\mathrm{2}{x}+\mathrm{3}}{{x}}\right) \\ $$$$\mathrm{ln}\:{y}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{ln}\:\left(\frac{\mathrm{2}{x}+\mathrm{3}}{{x}}\right)}{\mathrm{4}{x}−\mathrm{2}} \\ $$$$\mathrm{ln}\:{y}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{{d}}{{dx}}\left(\mathrm{ln}\:\left(\frac{\mathrm{2}{x}+\mathrm{3}}{{x}}\right)\right)}{\frac{{d}}{{dx}}\left(\mathrm{4}{x}−\mathrm{2}\right)} \\ $$$$\mathrm{ln}\:{y}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\frac{{x}}{\mathrm{2}{x}+\mathrm{3}}\right)\left(−\frac{\mathrm{3}}{{x}^{\mathrm{2}} }\right)}{\mathrm{4}}=\infty \\ $$$${therefore}\:{y}\:=\:{e}^{\infty} =\:\infty \\ $$

Commented by Dwaipayan Shikari last updated on 08/Aug/20

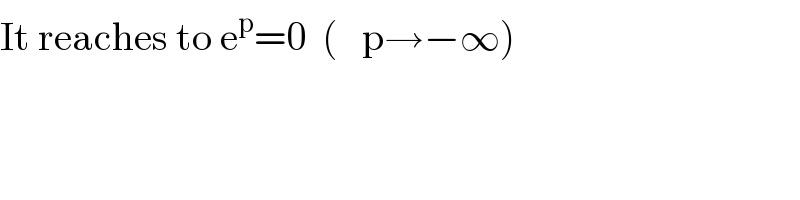
It reaches to e^p =0 ( p→−∞)

$$\mathrm{It}\:\mathrm{reaches}\:\mathrm{to}\:\mathrm{e}^{\mathrm{p}} =\mathrm{0}\:\:\left(\:\:\:\mathrm{p}\rightarrow−\infty\right) \\ $$

Answered by mathmax by abdo last updated on 08/Aug/20

let f(x) =(2+(3/x))^(1/(4x−2)) ⇒f(x) =e^((1/(4x−2))ln(2+(3/x))) ⇒ f(x) =e^((1/(x(4−(2/x))))ln(2+(3/x))) we do tbe changement (1/x)=t (x→0^(+ ) ⇒t →+∞) ⇒f(x) =e^((t/(4−2t))ln(2+3t)) but lim_(t→+∞) (t/(4−2t))ln(3t+2) =lim_(t→+∞) −(1/2)ln(3t+2) =−∞ ⇒ lim_(x→0) f(x) =0

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\left(\mathrm{2}+\frac{\mathrm{3}}{\mathrm{x}}\right)^{\frac{\mathrm{1}}{\mathrm{4x}−\mathrm{2}}} \:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{4x}−\mathrm{2}}\mathrm{ln}\left(\mathrm{2}+\frac{\mathrm{3}}{\mathrm{x}}\right)} \:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}\left(\mathrm{4}−\frac{\mathrm{2}}{\mathrm{x}}\right)}\mathrm{ln}\left(\mathrm{2}+\frac{\mathrm{3}}{\mathrm{x}}\right)} \:\mathrm{we}\:\mathrm{do}\:\mathrm{tbe}\:\mathrm{changement}\:\frac{\mathrm{1}}{\mathrm{x}}=\mathrm{t}\: \\ $$$$\left(\mathrm{x}\rightarrow\mathrm{0}^{+\:} \:\Rightarrow\mathrm{t}\:\rightarrow+\infty\right)\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{e}^{\frac{\mathrm{t}}{\mathrm{4}−\mathrm{2t}}\mathrm{ln}\left(\mathrm{2}+\mathrm{3t}\right)} \:\:\mathrm{but} \\ $$$$\mathrm{lim}_{\mathrm{t}\rightarrow+\infty} \:\frac{\mathrm{t}}{\mathrm{4}−\mathrm{2t}}\mathrm{ln}\left(\mathrm{3t}+\mathrm{2}\right)\:=\mathrm{lim}_{\mathrm{t}\rightarrow+\infty} −\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{3t}+\mathrm{2}\right)\:=−\infty\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com