
Question and Answers Forum
Question Number 107036 by john santu last updated on 08/Aug/20
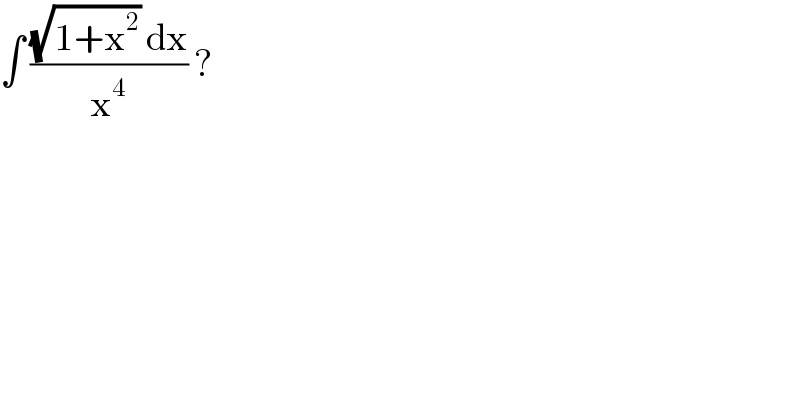
Commented by kaivan.ahmadi last updated on 08/Aug/20
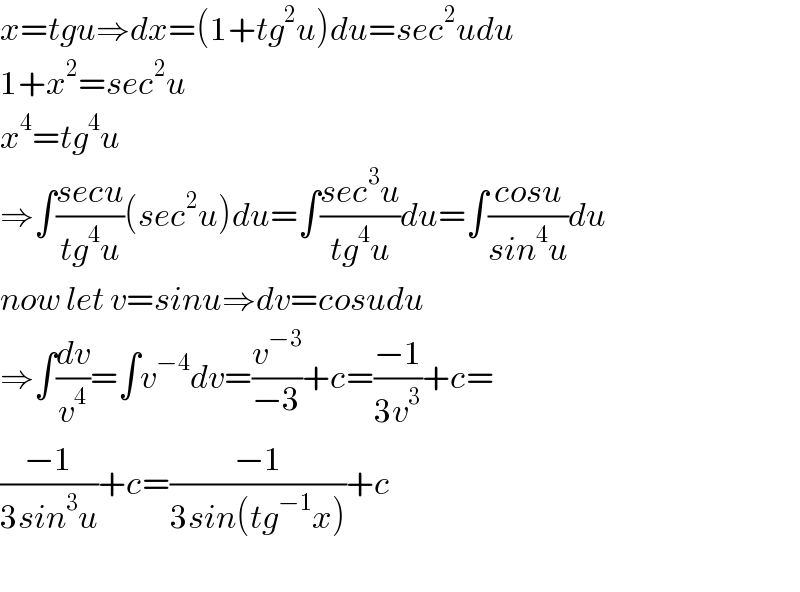
Answered by Dwaipayan Shikari last updated on 08/Aug/20
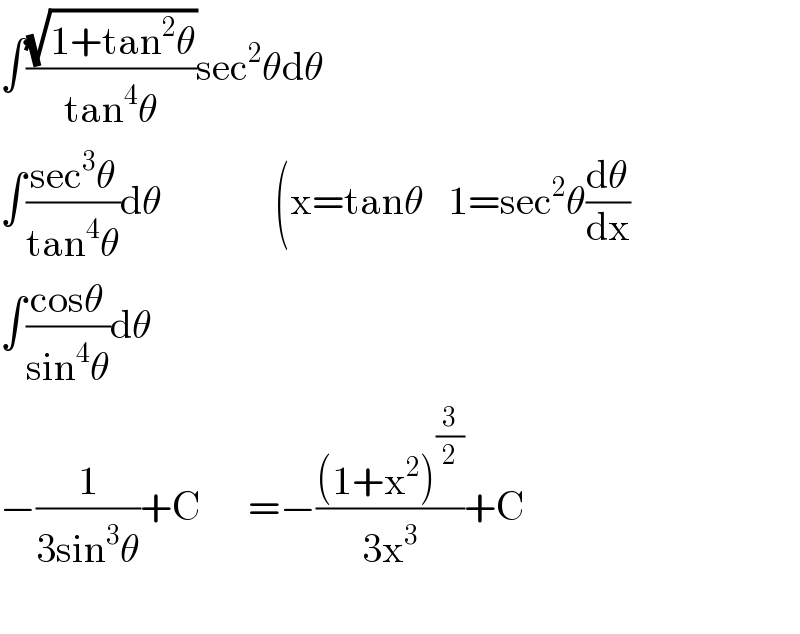
Answered by bobhans last updated on 08/Aug/20
![^� bobhans^� ∫ ((√(x^2 (1+(1/x^2 ))))/x^4 ) dx= ∫ ((x(√(1+(1/x^2 ))) dx)/x^4 ) =∫ ((√(1+(1/x^2 )))/x^3 ) dx . [ let u = 1+(1/x^2 ) ] du = −2x^(−3) dx ⇒ (dx/x^3 ) = −(du/2) −∫ (u^(1/2) /2) du = −(1/2)×(2/3)u^(3/2) +c −(1/3)(√((1+(1/x^2 ))^3 ))+c = −((x^2 +1)/(3x^2 ))×((√(x^2 +1))/x)+c =−(((x^2 +1)(√(x^2 +1)))/(3x^3 )) + c](Q107039.png)
| ||
Question and Answers Forum | ||
Question Number 107036 by john santu last updated on 08/Aug/20 | ||
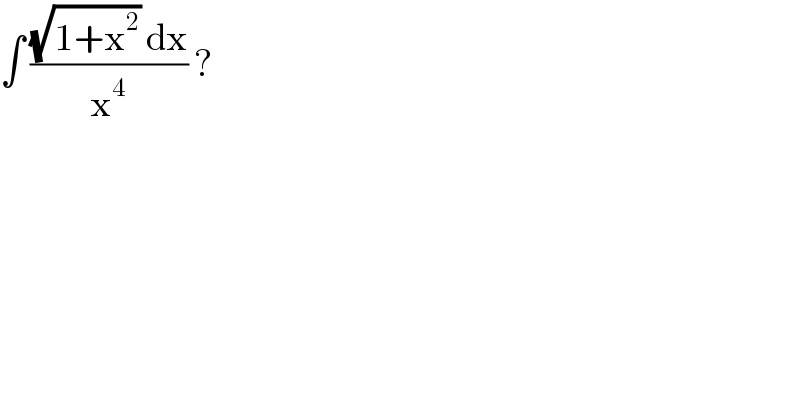 | ||
Commented by kaivan.ahmadi last updated on 08/Aug/20 | ||
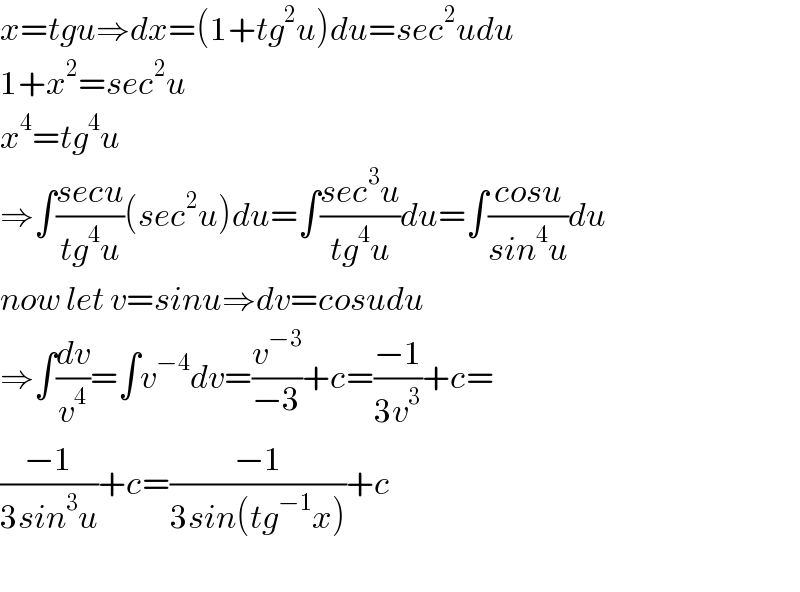 | ||
Answered by Dwaipayan Shikari last updated on 08/Aug/20 | ||
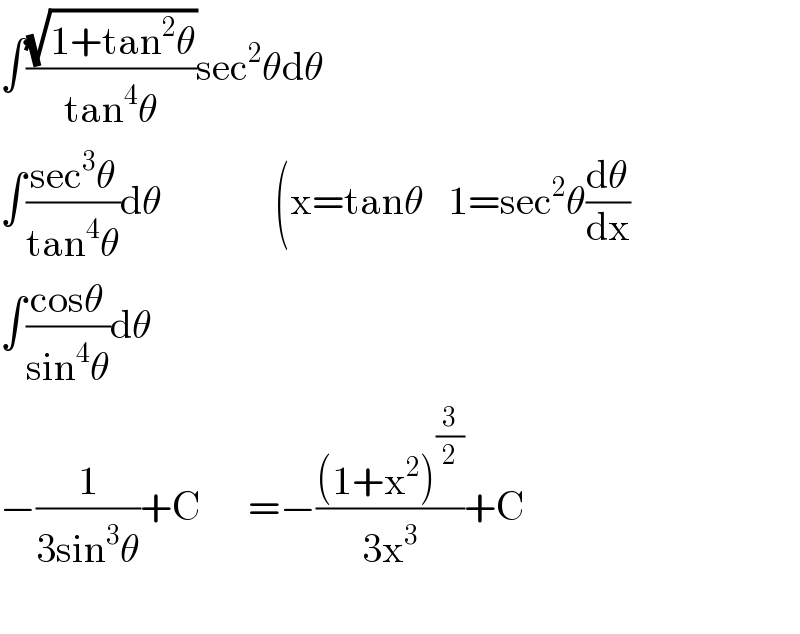 | ||
| ||
Answered by bobhans last updated on 08/Aug/20 | ||
![^� bobhans^� ∫ ((√(x^2 (1+(1/x^2 ))))/x^4 ) dx= ∫ ((x(√(1+(1/x^2 ))) dx)/x^4 ) =∫ ((√(1+(1/x^2 )))/x^3 ) dx . [ let u = 1+(1/x^2 ) ] du = −2x^(−3) dx ⇒ (dx/x^3 ) = −(du/2) −∫ (u^(1/2) /2) du = −(1/2)×(2/3)u^(3/2) +c −(1/3)(√((1+(1/x^2 ))^3 ))+c = −((x^2 +1)/(3x^2 ))×((√(x^2 +1))/x)+c =−(((x^2 +1)(√(x^2 +1)))/(3x^3 )) + c](Q107039.png) | ||
| ||