
Question and Answers Forum
Question Number 107069 by mathdave last updated on 08/Aug/20

Answered by bemath last updated on 09/Aug/20
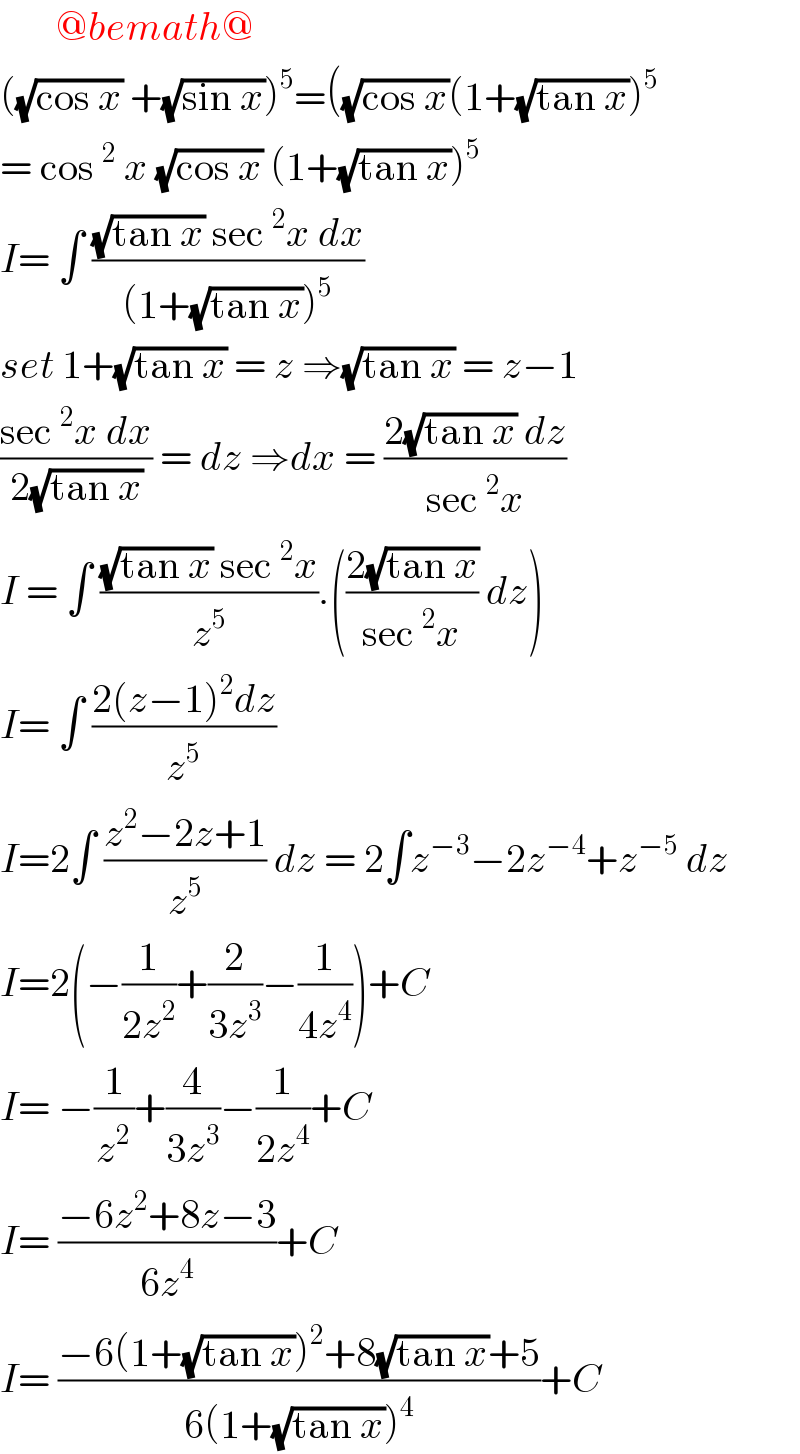
Commented by bobhans last updated on 09/Aug/20
![I = [((−6(1+(√(tan x)))^2 +8(√(tan x))+5)/(6(1+(√(tan x)))^4 )) ]_0 ^(π/4) I= [((−6(4)+8+5)/(6.16))]−[((−6+5)/6)] I= −((11)/(96))+(1/6)= ((−11+16)/(96)) = (5/(96))](Q107079.png)
Answered by Tony6400 last updated on 08/Aug/20
![Evaluate ∫_0 ^(π/4) (((√(sinx))dx)/(((√(cosx))+(√(sinx)))^5 )) Take ((√(cosx))+(√(sinx)))^5 =[(√(cosx))(1+((√(sinx))/(√(cosx))))]^5 =[(√(cosx))]^4 .(√(cosx))[1+(√(tanx))]^5 =cos^2 x(√(cosx))(1+(√(tanx)))^5 ∴I=∫_0 ^(π/4) ((√(sinx))/(cos^2 x(√(cosx))(1+(√(tanx)))^5 ))dx ⇒I=∫_0 ^(π/4) (((√(tanx)).sec^2 x)/((1+(√(tanx)))^5 ))dx Let w=1+(√(tanx))⇒(dw/dx)=((sec^2 x)/(2(√(tanx))))⇒dx=((2(√(tanx)))/(sec^2 x))dw When x=(π/4),w=2.When x=0,w=1⇒I=∫_1 ^2 (((√(tanx)).sec^2 x)/w^5 ).((2(√(tanx)))/(sec^2 x))dw I=2∫_1 ^2 ((tanx)/w^5 )dw=2∫_1 ^2 (((w−1)^2 )/w^5 )dw ∴I=2∫_1 ^2 ((w^2 −2w+1)/w^5 )dw=2∫_1 ^2 [w^(−3) −2w^(−4) +w^(−5) ]dw ⇒I=2(−(w^(−2) /2)+(2/3)w^(−3) −(w^(−4) /4))_1 ^2 ⇒I=2[−(1/(2w^2 ))+(2/(3w^3 ))−(1/(4w^4 ))]_1 ^2 =2[(−(1/(2(2)^2 ))+(2/(3(2)^3 ))−(1/(4(2)^4 )))−(((−1)/(2(1)^2 ))+(2/(3(1)^3 ))−(1/(4(1)^4 )))] I=2[((−1)/8)+(2/(24))−(1/(64))+(1/2)−(2/3)+(1/4)]=2((5/(192))) ⇒I=(5/(96))⇒∫_0 ^(π/4) ((√(sinx))/(((√(cosx))+(√(sinx)))^5 ))dx=(5/(96))](Q107111.png)
| ||
Question and Answers Forum | ||
Question Number 107069 by mathdave last updated on 08/Aug/20 | ||
 | ||
Answered by bemath last updated on 09/Aug/20 | ||
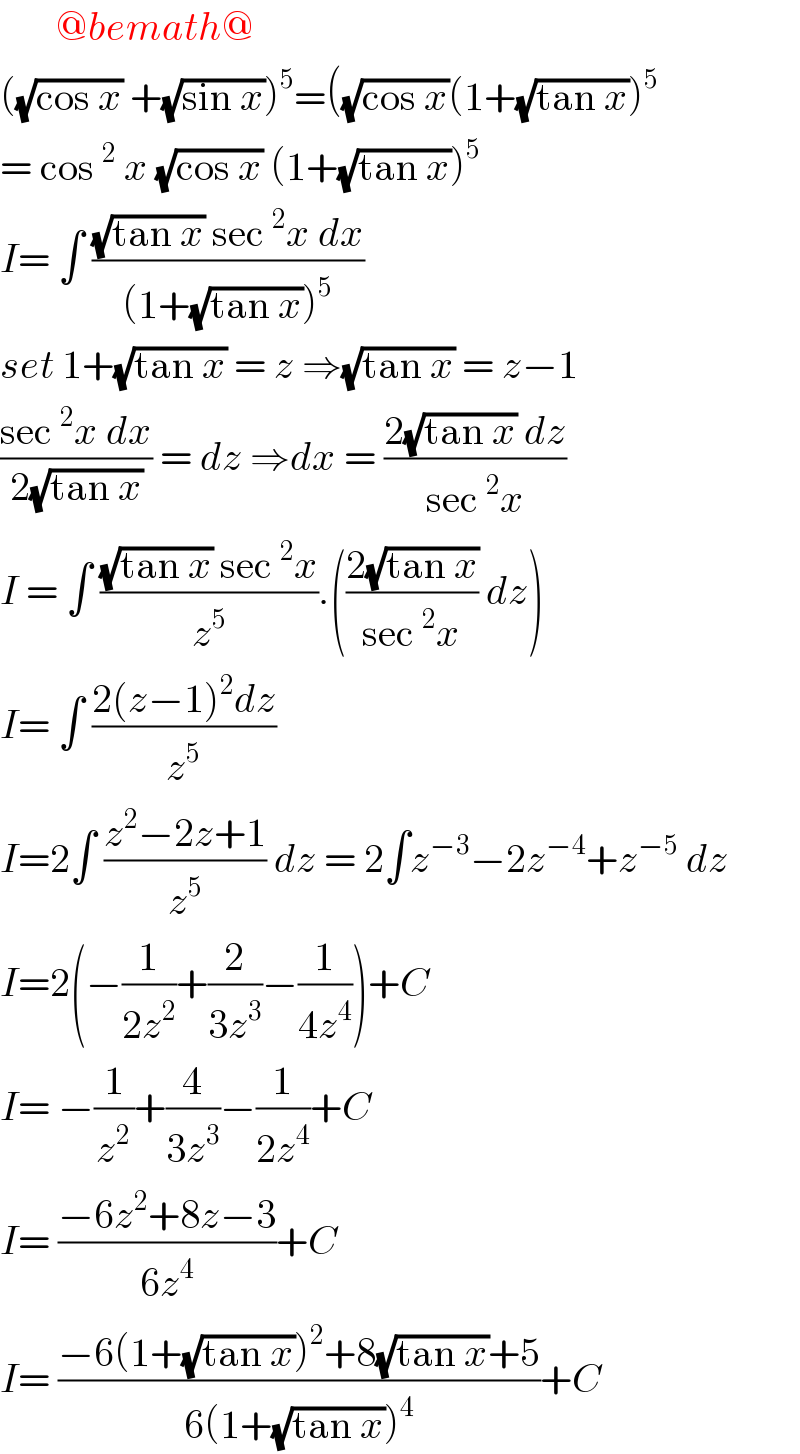 | ||
| ||
Commented by bobhans last updated on 09/Aug/20 | ||
![I = [((−6(1+(√(tan x)))^2 +8(√(tan x))+5)/(6(1+(√(tan x)))^4 )) ]_0 ^(π/4) I= [((−6(4)+8+5)/(6.16))]−[((−6+5)/6)] I= −((11)/(96))+(1/6)= ((−11+16)/(96)) = (5/(96))](Q107079.png) | ||
Answered by Tony6400 last updated on 08/Aug/20 | ||
![Evaluate ∫_0 ^(π/4) (((√(sinx))dx)/(((√(cosx))+(√(sinx)))^5 )) Take ((√(cosx))+(√(sinx)))^5 =[(√(cosx))(1+((√(sinx))/(√(cosx))))]^5 =[(√(cosx))]^4 .(√(cosx))[1+(√(tanx))]^5 =cos^2 x(√(cosx))(1+(√(tanx)))^5 ∴I=∫_0 ^(π/4) ((√(sinx))/(cos^2 x(√(cosx))(1+(√(tanx)))^5 ))dx ⇒I=∫_0 ^(π/4) (((√(tanx)).sec^2 x)/((1+(√(tanx)))^5 ))dx Let w=1+(√(tanx))⇒(dw/dx)=((sec^2 x)/(2(√(tanx))))⇒dx=((2(√(tanx)))/(sec^2 x))dw When x=(π/4),w=2.When x=0,w=1⇒I=∫_1 ^2 (((√(tanx)).sec^2 x)/w^5 ).((2(√(tanx)))/(sec^2 x))dw I=2∫_1 ^2 ((tanx)/w^5 )dw=2∫_1 ^2 (((w−1)^2 )/w^5 )dw ∴I=2∫_1 ^2 ((w^2 −2w+1)/w^5 )dw=2∫_1 ^2 [w^(−3) −2w^(−4) +w^(−5) ]dw ⇒I=2(−(w^(−2) /2)+(2/3)w^(−3) −(w^(−4) /4))_1 ^2 ⇒I=2[−(1/(2w^2 ))+(2/(3w^3 ))−(1/(4w^4 ))]_1 ^2 =2[(−(1/(2(2)^2 ))+(2/(3(2)^3 ))−(1/(4(2)^4 )))−(((−1)/(2(1)^2 ))+(2/(3(1)^3 ))−(1/(4(1)^4 )))] I=2[((−1)/8)+(2/(24))−(1/(64))+(1/2)−(2/3)+(1/4)]=2((5/(192))) ⇒I=(5/(96))⇒∫_0 ^(π/4) ((√(sinx))/(((√(cosx))+(√(sinx)))^5 ))dx=(5/(96))](Q107111.png) | ||
| ||