Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 107212 by bemath last updated on 09/Aug/20

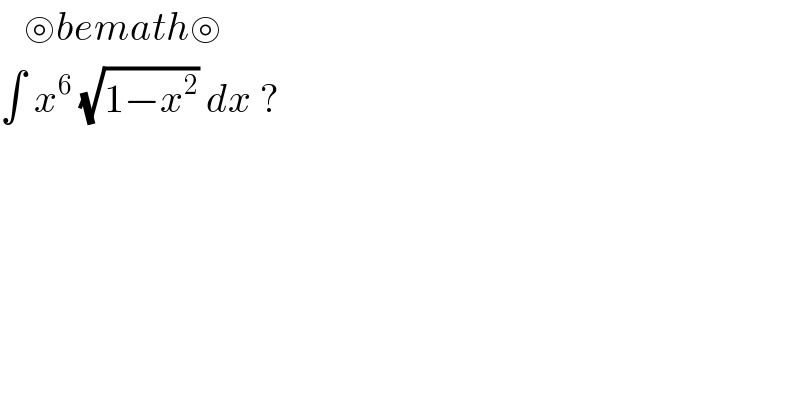
⊚bemath⊚ ∫ x^6 (√(1−x^2 )) dx ?

$$\:\:\:\circledcirc{bemath}\circledcirc \\ $$$$\int\:{x}^{\mathrm{6}} \:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:{dx}\:? \\ $$

Answered by Ar Brandon last updated on 09/Aug/20

I=∫x^6 (√(1−x^2 ))dx , x=sinθ I=∫sin^6 θcos^2 θdθ=∫(sin^6 θ−sin^8 θ)dθ (z−(1/z))^6 =(2isinθ)^6 , z=cosθ+isinθ z^6 −6z^5 ((1/z))+15z^4 ((1/z^2 ))−20z^3 ((1/z^3 ))+15z^2 ((1/z^4 ))−6z((1/z^5 ))+(1/z^6 )=−64sin^6 θ z^6 +(1/z^6 )−6(z^4 +(1/z^4 ))+15(z^2 +(1/z^2 ))−20=−64sin^6 θ 2cos6θ−12cos4θ+30cos2θ−20=−64sin^6 θ (z−(1/z))^8 =(2isinθ)^8 1 7 21 35 35 21 7 1 1 8 28 56 70 56 28 8 1 z^8 +(1/z^8 )−8(z^6 +(1/z^6 ))+28(z^4 +(1/z^4 ))−56(z^2 +(1/z^2 ))+70=256sin^8 θ 2cos8θ−16cos6θ+56cos4θ−112cos2θ+70=256sin^8 θ ⇒I=−(1/(64))[(2/6)sin6θ−((12)/4)sin4θ+((30)/2)sin2θ−20θ] −(1/(256))[(2/8)sin8θ−((16)/6)sin6θ+((56)/4)sin4θ−((112)/2)sin2θ+70θ]+C I=(1/(256))[10θ−4sin2θ−2sin4θ+(4/3)sin6θ−(1/4)sin8θ]+C

$$\mathcal{I}=\int\mathrm{x}^{\mathrm{6}} \sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:,\:\mathrm{x}=\mathrm{sin}\theta \\ $$$$\mathcal{I}=\int\mathrm{sin}^{\mathrm{6}} \theta\mathrm{cos}^{\mathrm{2}} \theta\mathrm{d}\theta=\int\left(\mathrm{sin}^{\mathrm{6}} \theta−\mathrm{sin}^{\mathrm{8}} \theta\right)\mathrm{d}\theta \\ $$$$\left(\mathrm{z}−\frac{\mathrm{1}}{\mathrm{z}}\right)^{\mathrm{6}} =\left(\mathrm{2isin}\theta\right)^{\mathrm{6}} \:,\:\mathrm{z}=\mathrm{cos}\theta+\mathrm{isin}\theta \\ $$$$\mathrm{z}^{\mathrm{6}} −\mathrm{6z}^{\mathrm{5}} \left(\frac{\mathrm{1}}{\mathrm{z}}\right)+\mathrm{15z}^{\mathrm{4}} \left(\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{2}} }\right)−\mathrm{20z}^{\mathrm{3}} \left(\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{3}} }\right)+\mathrm{15z}^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{4}} }\right)−\mathrm{6z}\left(\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{5}} }\right)+\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{6}} }=−\mathrm{64sin}^{\mathrm{6}} \theta \\ $$$$\mathrm{z}^{\mathrm{6}} +\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{6}} }−\mathrm{6}\left(\mathrm{z}^{\mathrm{4}} +\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{4}} }\right)+\mathrm{15}\left(\mathrm{z}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{2}} }\right)−\mathrm{20}=−\mathrm{64sin}^{\mathrm{6}} \theta \\ $$$$\mathrm{2cos6}\theta−\mathrm{12cos4}\theta+\mathrm{30cos2}\theta−\mathrm{20}=−\mathrm{64sin}^{\mathrm{6}} \theta \\ $$$$\left(\mathrm{z}−\frac{\mathrm{1}}{\mathrm{z}}\right)^{\mathrm{8}} =\left(\mathrm{2isin}\theta\right)^{\mathrm{8}} \\ $$$$\mathrm{1}\:\mathrm{7}\:\mathrm{21}\:\mathrm{35}\:\mathrm{35}\:\mathrm{21}\:\mathrm{7}\:\mathrm{1}\:\:\:\mathrm{1}\:\mathrm{8}\:\mathrm{28}\:\mathrm{56}\:\mathrm{70}\:\mathrm{56}\:\mathrm{28}\:\mathrm{8}\:\mathrm{1}\: \\ $$$$\mathrm{z}^{\mathrm{8}} +\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{8}} }−\mathrm{8}\left(\mathrm{z}^{\mathrm{6}} +\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{6}} }\right)+\mathrm{28}\left(\mathrm{z}^{\mathrm{4}} +\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{4}} }\right)−\mathrm{56}\left(\mathrm{z}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{2}} }\right)+\mathrm{70}=\mathrm{256sin}^{\mathrm{8}} \theta \\ $$$$\mathrm{2cos8}\theta−\mathrm{16cos6}\theta+\mathrm{56cos4}\theta−\mathrm{112cos2}\theta+\mathrm{70}=\mathrm{256sin}^{\mathrm{8}} \theta \\ $$$$\Rightarrow\mathcal{I}=−\frac{\mathrm{1}}{\mathrm{64}}\left[\frac{\mathrm{2}}{\mathrm{6}}\mathrm{sin6}\theta−\frac{\mathrm{12}}{\mathrm{4}}\mathrm{sin4}\theta+\frac{\mathrm{30}}{\mathrm{2}}\mathrm{sin2}\theta−\mathrm{20}\theta\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:−\frac{\mathrm{1}}{\mathrm{256}}\left[\frac{\mathrm{2}}{\mathrm{8}}\mathrm{sin8}\theta−\frac{\mathrm{16}}{\mathrm{6}}\mathrm{sin6}\theta+\frac{\mathrm{56}}{\mathrm{4}}\mathrm{sin4}\theta−\frac{\mathrm{112}}{\mathrm{2}}\mathrm{sin2}\theta+\mathrm{70}\theta\right]+\mathcal{C} \\ $$$$\mathcal{I}=\frac{\mathrm{1}}{\mathrm{256}}\left[\mathrm{10}\theta−\mathrm{4sin2}\theta−\mathrm{2sin4}\theta+\frac{\mathrm{4}}{\mathrm{3}}\mathrm{sin6}\theta−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin8}\theta\right]+\mathcal{C} \\ $$

Answered by bobhans last updated on 09/Aug/20

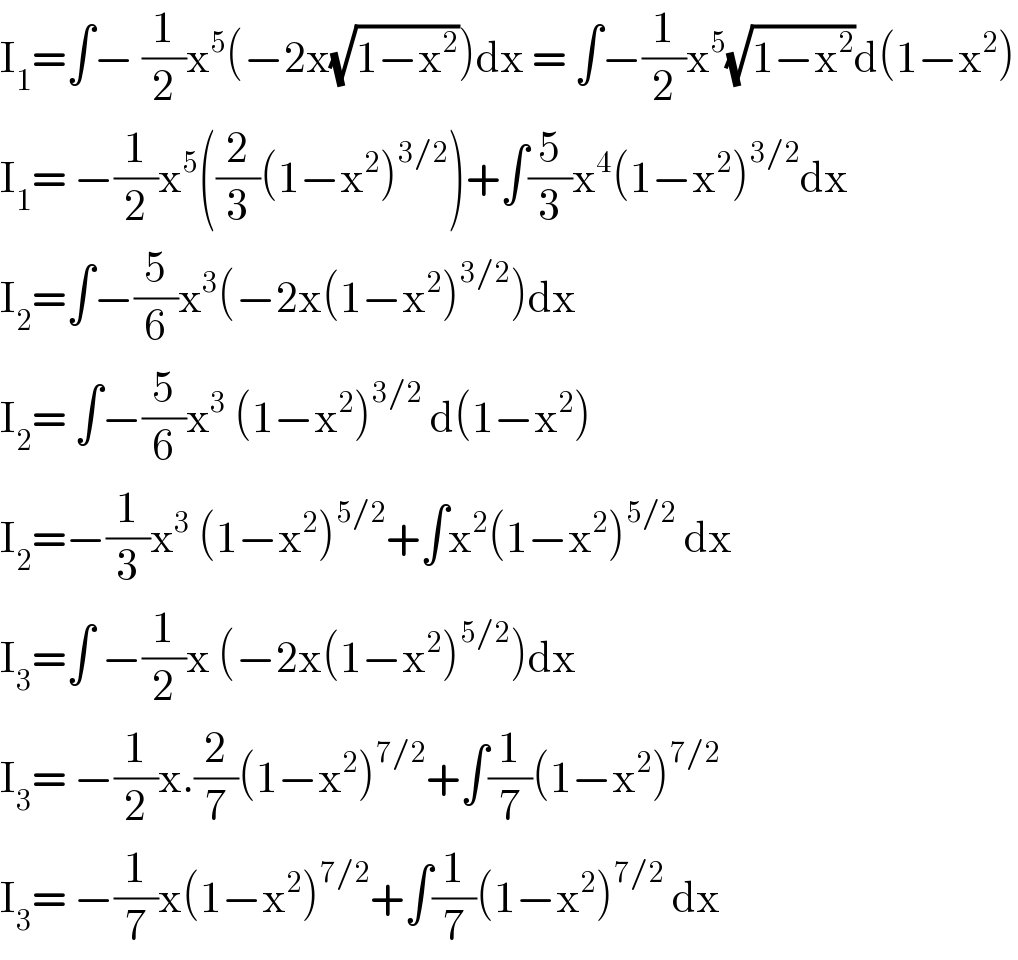
I_1 =∫− (1/2)x^5 (−2x(√(1−x^2 )))dx = ∫−(1/2)x^5 (√(1−x^2 ))d(1−x^2 ) I_1 = −(1/2)x^5 ((2/3)(1−x^2 )^(3/2) )+∫(5/3)x^4 (1−x^2 )^(3/2) dx I_2 =∫−(5/6)x^3 (−2x(1−x^2 )^(3/2) )dx I_2 = ∫−(5/6)x^3 (1−x^2 )^(3/2) d(1−x^2 ) I_2 =−(1/3)x^3 (1−x^2 )^(5/2) +∫x^2 (1−x^2 )^(5/2) dx I_3 =∫ −(1/2)x (−2x(1−x^2 )^(5/2) )dx I_3 = −(1/2)x.(2/7)(1−x^2 )^(7/2) +∫(1/7)(1−x^2 )^(7/2) I_3 = −(1/7)x(1−x^2 )^(7/2) +∫(1/7)(1−x^2 )^(7/2) dx

$$\mathrm{I}_{\mathrm{1}} =\int−\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{5}} \left(−\mathrm{2x}\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\right)\mathrm{dx}\:=\:\int−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{5}} \sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\mathrm{d}\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right) \\ $$$$\mathrm{I}_{\mathrm{1}} =\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{5}} \left(\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} \right)+\int\frac{\mathrm{5}}{\mathrm{3}}\mathrm{x}^{\mathrm{4}} \left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} \mathrm{dx} \\ $$$$\mathrm{I}_{\mathrm{2}} =\int−\frac{\mathrm{5}}{\mathrm{6}}\mathrm{x}^{\mathrm{3}} \left(−\mathrm{2x}\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} \right)\mathrm{dx} \\ $$$$\mathrm{I}_{\mathrm{2}} =\:\int−\frac{\mathrm{5}}{\mathrm{6}}\mathrm{x}^{\mathrm{3}} \:\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} \:\mathrm{d}\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right) \\ $$$$\mathrm{I}_{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x}^{\mathrm{3}} \:\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{5}/\mathrm{2}} +\int\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{5}/\mathrm{2}} \:\mathrm{dx} \\ $$$$\mathrm{I}_{\mathrm{3}} =\int\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\:\left(−\mathrm{2x}\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{5}/\mathrm{2}} \right)\mathrm{dx} \\ $$$$\mathrm{I}_{\mathrm{3}} =\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}.\frac{\mathrm{2}}{\mathrm{7}}\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{7}/\mathrm{2}} +\int\frac{\mathrm{1}}{\mathrm{7}}\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{7}/\mathrm{2}} \\ $$$$\mathrm{I}_{\mathrm{3}} =\:−\frac{\mathrm{1}}{\mathrm{7}}\mathrm{x}\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{7}/\mathrm{2}} +\int\frac{\mathrm{1}}{\mathrm{7}}\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{7}/\mathrm{2}} \:\mathrm{dx} \\ $$

Answered by 1549442205PVT last updated on 10/Aug/20

Set (1/x^2 )−1=u^2 ⇒2udu=−(2/x^3 )dx ⇒dx=−ux^3 du,(√(1−x^2 ))=ux,x^2 =(1/(u^2 +1)) F=−∫x^6 .(ux)(ux^3 )du=−∫x^(10) u^2 du =−∫((u^2 du)/((1+u^2 )^5 ))=−∫((u^2 +1−1)/((u^2 +1)^5 ))du =−∫(du/((1+u^2 )^4 ))+∫(du/((1+u^2 )^5 ))=I_5 −I_4 Apply the current formula: I_n =(1/(2a^2 (n−1))).(t/((t^2 +a^2 )^(n−1) ))+(1/a^2 ).((2n−3)/(2n−2)).I_(n−1) I_4 =(1/6).(u/((u^2 +1)^3 ))+(5/6)I_3 = (u/(6(u^2 +1)^3 ))+(5/6)[(1/4).(u/((u^2 +1)^2 ))+(3/4).I_2 ] =(u/(6(u^2 +1)^3 ))+((5u)/(24(u^2 +1)^2 ))+(5/8)I_2 =(u/(6(u^2 +1)^3 ))+((5u)/(24(u^2 +1)^2 ))+(5/8)[(1/2).(u/((u^2 +1)))+(1/2)∫(du/(u^2 +1))] =(u/(6(u^2 +1)^3 ))+((5u)/(24(u^2 +1)^2 ))+((5u)/(16(u^2 +1)))+(5/(16))tan^(−1) (u) I_5 =(1/8).(u/((u^2 +1)^4 ))+(7/8).I_4 .Therefore, F=I_5 −I_4 =(1/8).(u/((u^2 +1)^4 ))−(1/8)I_4 =(u/(8(u^2 +1)^4 ))−(1/8)[(u/(6(u^2 +1)^3 ))+((5u)/(24(u^2 +1)^2 ))+((5u)/(16(u^2 +1)))+(5/(16))tan^(−1) (u)]+C =(u/(8(u^2 +1)^4 ))−(u/(48(u^2 +1)^3 ))−((5u)/(192(u^2 +1)^2 )) −((5u)/(128(u^2 +1)))−(5/(128))tan^(−1) (u)+C Substituting u^2 +1=1/x^2 and u=((√(1−x^2 ))/x) we get: F=((x^7 (√(1−x^2 )))/8)−((x^5 (√(1−x^2 )))/(48))−((5x^3 (√(1−x^2 )))/(192)) −((5x(√(1−x^2 )))/(128))−(5/(128))tan^(−1) (((√(1−x^2 ))/x)) +C

$$\mathrm{Set}\:\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }−\mathrm{1}=\mathrm{u}^{\mathrm{2}} \Rightarrow\mathrm{2udu}=−\frac{\mathrm{2}}{\mathrm{x}^{\mathrm{3}} }\mathrm{dx} \\ $$$$\Rightarrow\mathrm{dx}=−\mathrm{ux}^{\mathrm{3}} \mathrm{du},\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }=\mathrm{ux},\mathrm{x}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\mathrm{F}=−\int\mathrm{x}^{\mathrm{6}} .\left(\mathrm{ux}\right)\left(\mathrm{ux}^{\mathrm{3}} \right)\mathrm{du}=−\int\mathrm{x}^{\mathrm{10}} \mathrm{u}^{\mathrm{2}} \mathrm{du} \\ $$$$=−\int\frac{\mathrm{u}^{\mathrm{2}} \mathrm{du}}{\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)^{\mathrm{5}} }=−\int\frac{\mathrm{u}^{\mathrm{2}} +\mathrm{1}−\mathrm{1}}{\left(\mathrm{u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{5}} }\mathrm{du} \\ $$$$=−\int\frac{\mathrm{du}}{\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)^{\mathrm{4}} }+\int\frac{\mathrm{du}}{\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)^{\mathrm{5}} }=\mathrm{I}_{\mathrm{5}} −\mathrm{I}_{\mathrm{4}} \\ $$$$ \\ $$$$\mathrm{Apply}\:\mathrm{the}\:\mathrm{current}\:\mathrm{formula}: \\ $$$$\mathrm{I}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{2a}^{\mathrm{2}} \left(\mathrm{n}−\mathrm{1}\right)}.\frac{\mathrm{t}}{\left(\mathrm{t}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} \right)^{\mathrm{n}−\mathrm{1}} }+\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }.\frac{\mathrm{2n}−\mathrm{3}}{\mathrm{2n}−\mathrm{2}}.\mathrm{I}_{\mathrm{n}−\mathrm{1}} \\ $$$$\mathrm{I}_{\mathrm{4}} =\frac{\mathrm{1}}{\mathrm{6}}.\frac{\mathrm{u}}{\left(\mathrm{u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }+\frac{\mathrm{5}}{\mathrm{6}}\mathrm{I}_{\mathrm{3}} = \\ $$$$\frac{\mathrm{u}}{\mathrm{6}\left(\mathrm{u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }+\frac{\mathrm{5}}{\mathrm{6}}\left[\frac{\mathrm{1}}{\mathrm{4}}.\frac{\mathrm{u}}{\left(\mathrm{u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{3}}{\mathrm{4}}.\mathrm{I}_{\mathrm{2}} \right] \\ $$$$=\frac{\mathrm{u}}{\mathrm{6}\left(\mathrm{u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }+\frac{\mathrm{5u}}{\mathrm{24}\left(\mathrm{u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{5}}{\mathrm{8}}\mathrm{I}_{\mathrm{2}} \\ $$$$=\frac{\mathrm{u}}{\mathrm{6}\left(\mathrm{u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }+\frac{\mathrm{5u}}{\mathrm{24}\left(\mathrm{u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{5}}{\mathrm{8}}\left[\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{u}}{\left(\mathrm{u}^{\mathrm{2}} +\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} +\mathrm{1}}\right] \\ $$$$=\frac{\mathrm{u}}{\mathrm{6}\left(\mathrm{u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }+\frac{\mathrm{5u}}{\mathrm{24}\left(\mathrm{u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{5u}}{\mathrm{16}\left(\mathrm{u}^{\mathrm{2}} +\mathrm{1}\right)}+\frac{\mathrm{5}}{\mathrm{16}}\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{u}\right) \\ $$$$\mathrm{I}_{\mathrm{5}} =\frac{\mathrm{1}}{\mathrm{8}}.\frac{\mathrm{u}}{\left(\mathrm{u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{4}} }+\frac{\mathrm{7}}{\mathrm{8}}.\mathrm{I}_{\mathrm{4}} .\mathrm{Therefore}, \\ $$$$\mathrm{F}=\mathrm{I}_{\mathrm{5}} −\mathrm{I}_{\mathrm{4}} =\frac{\mathrm{1}}{\mathrm{8}}.\frac{\mathrm{u}}{\left(\mathrm{u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{4}} }−\frac{\mathrm{1}}{\mathrm{8}}\mathrm{I}_{\mathrm{4}} \\ $$$$=\frac{\mathrm{u}}{\mathrm{8}\left(\mathrm{u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{4}} }−\frac{\mathrm{1}}{\mathrm{8}}\left[\frac{\mathrm{u}}{\mathrm{6}\left(\mathrm{u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }+\frac{\mathrm{5u}}{\mathrm{24}\left(\mathrm{u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{5u}}{\mathrm{16}\left(\mathrm{u}^{\mathrm{2}} +\mathrm{1}\right)}+\frac{\mathrm{5}}{\mathrm{16}}\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{u}\right)\right]+\mathrm{C} \\ $$$$=\frac{\boldsymbol{\mathrm{u}}}{\mathrm{8}\left(\boldsymbol{\mathrm{u}}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{4}} }−\frac{\boldsymbol{\mathrm{u}}}{\mathrm{48}\left(\boldsymbol{\mathrm{u}}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }−\frac{\mathrm{5}\boldsymbol{\mathrm{u}}}{\mathrm{192}\left(\boldsymbol{\mathrm{u}}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\: \\ $$$$−\frac{\mathrm{5}\boldsymbol{\mathrm{u}}}{\mathrm{128}\left(\boldsymbol{\mathrm{u}}^{\mathrm{2}} +\mathrm{1}\right)}−\frac{\mathrm{5}}{\mathrm{128}}\boldsymbol{\mathrm{tan}}^{−\mathrm{1}} \left(\boldsymbol{\mathrm{u}}\right)+\mathrm{C} \\ $$$$\mathrm{Substituting}\:\mathrm{u}^{\mathrm{2}} +\mathrm{1}=\mathrm{1}/\mathrm{x}^{\mathrm{2}} \mathrm{and}\:\mathrm{u}=\frac{\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}{\mathrm{x}} \\ $$$$\mathrm{we}\:\mathrm{get}: \\ $$$$\boldsymbol{\mathrm{F}}=\frac{\boldsymbol{\mathrm{x}}^{\mathrm{7}} \sqrt{\mathrm{1}−\boldsymbol{\mathrm{x}}^{\mathrm{2}} }}{\mathrm{8}}−\frac{\boldsymbol{\mathrm{x}}^{\mathrm{5}} \sqrt{\mathrm{1}−\boldsymbol{\mathrm{x}}^{\mathrm{2}} }}{\mathrm{48}}−\frac{\mathrm{5}\boldsymbol{\mathrm{x}}^{\mathrm{3}} \sqrt{\mathrm{1}−\boldsymbol{\mathrm{x}}^{\mathrm{2}} }}{\mathrm{192}} \\ $$$$−\frac{\mathrm{5}\boldsymbol{\mathrm{x}}\sqrt{\mathrm{1}−\boldsymbol{\mathrm{x}}^{\mathrm{2}} }}{\mathrm{128}}−\frac{\mathrm{5}}{\mathrm{128}}\boldsymbol{\mathrm{tan}}^{−\mathrm{1}} \left(\frac{\sqrt{\mathrm{1}−\boldsymbol{\mathrm{x}}^{\mathrm{2}} }}{\boldsymbol{\mathrm{x}}}\right)\:+\mathrm{C} \\ $$

Answered by mathmax by abdo last updated on 10/Aug/20

A =∫ x^6 (√(1−x^2 ))dx we do the changement x =sint ⇒ A =∫ sin^6 t cos^2 t dt =∫ (sin^2 t)^3 (((1+cos(2t))/2))dt =(1/2)∫ (((1−cos(2t))/2))^3 (1+cos(2t))dt =(1/(16)) ∫ (1−cos(2t))^2 (1−cos^2 (2t))dt =(1/(16)) ∫ (1−2cos(2t)+cos^2 (2t))(1−((1+cos(4t))/2))dt =(1/(32))∫ (((1+cos(4t))/2)+1−2cos(2t))(1−cos(4t))dt =(1/(64))∫ (3+cos(4t)−4cos(2t))(1−cos(4t))dt =(1/(64))∫ (3−3cos(4t)+cos(4t)−cos^2 (4t)−4cos(2t)+4cos(2t)cos(4t))dt =(1/(64))∫ (3−2cos(4t)−((1+cos(8t))/2)−4cos(2t)+2{cos(6t) +cos(2t)})dt =(1/(128))∫ {6−4cos(4t)−1−cos(8t)−8cos(2t)+4cos(6t)+4cos(2t)}dt =(1/(128)) ∫ {5 −4cos(4t)−cos(8t)−4cos(2t)+4cos(6t)}dt =(5/(128))t −(4/(128))∫ cos(4t)dt−(1/(128))∫ cos(8t)dt−(4/(128))∫ cos(2t)dt +(4/(128))∫ cos(6t)dt =(5/(128))t −(1/(128))sin(4t)−(1/(8.128))sin(8t)−(1/(64)) sin(2t) +(4/(6.128))sin(6t) +C t =arcsinx

$$\mathrm{A}\:=\int\:\mathrm{x}^{\mathrm{6}} \sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{x}\:=\mathrm{sint}\:\Rightarrow \\ $$$$\mathrm{A}\:=\int\:\mathrm{sin}^{\mathrm{6}} \mathrm{t}\:\mathrm{cos}^{\mathrm{2}} \mathrm{t}\:\:\mathrm{dt}\:\:=\int\:\left(\mathrm{sin}^{\mathrm{2}} \mathrm{t}\right)^{\mathrm{3}} \left(\frac{\mathrm{1}+\mathrm{cos}\left(\mathrm{2t}\right)}{\mathrm{2}}\right)\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\:\left(\frac{\mathrm{1}−\mathrm{cos}\left(\mathrm{2t}\right)}{\mathrm{2}}\right)^{\mathrm{3}} \left(\mathrm{1}+\mathrm{cos}\left(\mathrm{2t}\right)\right)\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}\:\int\:\left(\mathrm{1}−\mathrm{cos}\left(\mathrm{2t}\right)\right)^{\mathrm{2}} \left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \left(\mathrm{2t}\right)\right)\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}\:\int\:\left(\mathrm{1}−\mathrm{2cos}\left(\mathrm{2t}\right)+\mathrm{cos}^{\mathrm{2}} \left(\mathrm{2t}\right)\right)\left(\mathrm{1}−\frac{\mathrm{1}+\mathrm{cos}\left(\mathrm{4t}\right)}{\mathrm{2}}\right)\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{32}}\int\:\left(\frac{\mathrm{1}+\mathrm{cos}\left(\mathrm{4t}\right)}{\mathrm{2}}+\mathrm{1}−\mathrm{2cos}\left(\mathrm{2t}\right)\right)\left(\mathrm{1}−\mathrm{cos}\left(\mathrm{4t}\right)\right)\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{64}}\int\:\left(\mathrm{3}+\mathrm{cos}\left(\mathrm{4t}\right)−\mathrm{4cos}\left(\mathrm{2t}\right)\right)\left(\mathrm{1}−\mathrm{cos}\left(\mathrm{4t}\right)\right)\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{64}}\int\:\left(\mathrm{3}−\mathrm{3cos}\left(\mathrm{4t}\right)+\mathrm{cos}\left(\mathrm{4t}\right)−\mathrm{cos}^{\mathrm{2}} \left(\mathrm{4t}\right)−\mathrm{4cos}\left(\mathrm{2t}\right)+\mathrm{4cos}\left(\mathrm{2t}\right)\mathrm{cos}\left(\mathrm{4t}\right)\right)\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{64}}\int\:\left(\mathrm{3}−\mathrm{2cos}\left(\mathrm{4t}\right)−\frac{\mathrm{1}+\mathrm{cos}\left(\mathrm{8t}\right)}{\mathrm{2}}−\mathrm{4cos}\left(\mathrm{2t}\right)+\mathrm{2}\left\{\mathrm{cos}\left(\mathrm{6t}\right)\:+\mathrm{cos}\left(\mathrm{2t}\right)\right\}\right)\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{128}}\int\:\:\left\{\mathrm{6}−\mathrm{4cos}\left(\mathrm{4t}\right)−\mathrm{1}−\mathrm{cos}\left(\mathrm{8t}\right)−\mathrm{8cos}\left(\mathrm{2t}\right)+\mathrm{4cos}\left(\mathrm{6t}\right)+\mathrm{4cos}\left(\mathrm{2t}\right)\right\}\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{128}}\:\int\:\left\{\mathrm{5}\:−\mathrm{4cos}\left(\mathrm{4t}\right)−\mathrm{cos}\left(\mathrm{8t}\right)−\mathrm{4cos}\left(\mathrm{2t}\right)+\mathrm{4cos}\left(\mathrm{6t}\right)\right\}\mathrm{dt} \\ $$$$=\frac{\mathrm{5}}{\mathrm{128}}\mathrm{t}\:−\frac{\mathrm{4}}{\mathrm{128}}\int\:\mathrm{cos}\left(\mathrm{4t}\right)\mathrm{dt}−\frac{\mathrm{1}}{\mathrm{128}}\int\:\mathrm{cos}\left(\mathrm{8t}\right)\mathrm{dt}−\frac{\mathrm{4}}{\mathrm{128}}\int\:\mathrm{cos}\left(\mathrm{2t}\right)\mathrm{dt} \\ $$$$+\frac{\mathrm{4}}{\mathrm{128}}\int\:\mathrm{cos}\left(\mathrm{6t}\right)\mathrm{dt} \\ $$$$=\frac{\mathrm{5}}{\mathrm{128}}\mathrm{t}\:−\frac{\mathrm{1}}{\mathrm{128}}\mathrm{sin}\left(\mathrm{4t}\right)−\frac{\mathrm{1}}{\mathrm{8}.\mathrm{128}}\mathrm{sin}\left(\mathrm{8t}\right)−\frac{\mathrm{1}}{\mathrm{64}}\:\mathrm{sin}\left(\mathrm{2t}\right)\:+\frac{\mathrm{4}}{\mathrm{6}.\mathrm{128}}\mathrm{sin}\left(\mathrm{6t}\right)\:+\mathrm{C} \\ $$$$\mathrm{t}\:=\mathrm{arcsinx} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com