
Previous in Relation and Functions Next in Relation and Functions
Question Number 107289 by mathmax by abdo last updated on 09/Aug/20
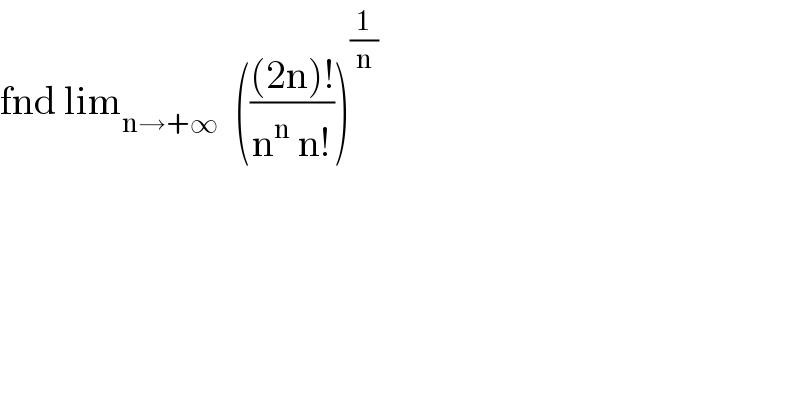
$$\mathrm{fnd}\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\:\left(\frac{\left(\mathrm{2n}\right)!}{\mathrm{n}^{\mathrm{n}} \:\mathrm{n}!}\right)^{\frac{\mathrm{1}}{\mathrm{n}}} \\ $$
Answered by Ar Brandon last updated on 13/Aug/20
![A_n = ((((2n)!)/(n^n n!)))^(1/n) lnA_n =ln ((((2n)!)/(n^n n!)))^(1/n) =(1/n)[ln(2n)!−ln(n^n )−ln(n!)] =(1/n)[lnΠ_(k=0) ^(2n−1) (2n−k)−lnΠ_(k=0) ^(n−1) (n−k)]−ln(n) =(1/n)[Σ_(k=0) ^(2n−1) ln(2n−k)−Σ_(k=0) ^(n−1) ln(n−k)]−ln(n) =(1/n)[2n∙ln(n)+Σ_(k=0) ^(2n−1) ln(2−(k/n))−n∙ln(n)−Σ_(k=0) ^(n−1) ln(1−(k/n))]−ln(n) lim_(n→∞) lnA_n =∫_0 ^2 ln(2−x)dx−∫_0 ^1 ln(1−x)dx =∫_0 ^2 ln(t_1 )dt_1 −∫_0 ^1 ln(t_2 )dt_2 =[tlnt−t]_1 ^2 =2ln2−1 lim_(n→∞) A_n =e^(2ln2−1) =(4/e)](Q107878.png)
$$\mathrm{A}_{\mathrm{n}} =\:\left(\frac{\left(\mathrm{2n}\right)!}{\mathrm{n}^{\mathrm{n}} \:\mathrm{n}!}\right)^{\frac{\mathrm{1}}{\mathrm{n}}} \\ $$$$\mathrm{lnA}_{\mathrm{n}} =\mathrm{ln}\:\left(\frac{\left(\mathrm{2n}\right)!}{\mathrm{n}^{\mathrm{n}} \:\mathrm{n}!}\right)^{\frac{\mathrm{1}}{\mathrm{n}}} =\frac{\mathrm{1}}{\mathrm{n}}\left[\mathrm{ln}\left(\mathrm{2n}\right)!−\mathrm{ln}\left(\mathrm{n}^{\mathrm{n}} \right)−\mathrm{ln}\left(\mathrm{n}!\right)\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{n}}\left[\mathrm{ln}\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{2n}−\mathrm{1}} {\prod}}\left(\mathrm{2n}−\mathrm{k}\right)−\mathrm{ln}\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}−\mathrm{1}} {\prod}}\left(\mathrm{n}−\mathrm{k}\right)\right]−\mathrm{ln}\left(\mathrm{n}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{n}}\left[\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{2n}−\mathrm{1}} {\sum}}\mathrm{ln}\left(\mathrm{2n}−\mathrm{k}\right)−\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}−\mathrm{1}} {\sum}}\mathrm{ln}\left(\mathrm{n}−\mathrm{k}\right)\right]−\mathrm{ln}\left(\mathrm{n}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{n}}\left[\mathrm{2n}\centerdot\mathrm{ln}\left(\mathrm{n}\right)+\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{2n}−\mathrm{1}} {\sum}}\mathrm{ln}\left(\mathrm{2}−\frac{\mathrm{k}}{\mathrm{n}}\right)−\mathrm{n}\centerdot\mathrm{ln}\left(\mathrm{n}\right)−\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}−\mathrm{1}} {\sum}}\mathrm{ln}\left(\mathrm{1}−\frac{\mathrm{k}}{\mathrm{n}}\right)\right]−\mathrm{ln}\left(\mathrm{n}\right) \\ $$$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}lnA}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{2}} \mathrm{ln}\left(\mathrm{2}−\mathrm{x}\right)\mathrm{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)\mathrm{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\int_{\mathrm{0}} ^{\mathrm{2}} \mathrm{ln}\left(\mathrm{t}_{\mathrm{1}} \right)\mathrm{dt}_{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{t}_{\mathrm{2}} \right)\mathrm{dt}_{\mathrm{2}} =\left[\mathrm{tlnt}−\mathrm{t}\right]_{\mathrm{1}} ^{\mathrm{2}} =\mathrm{2ln2}−\mathrm{1} \\ $$$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}A}_{\mathrm{n}} =\mathrm{e}^{\mathrm{2ln2}−\mathrm{1}} =\frac{\mathrm{4}}{\mathrm{e}} \\ $$
