
Question and Answers Forum
Question Number 107330 by saorey0202 last updated on 10/Aug/20
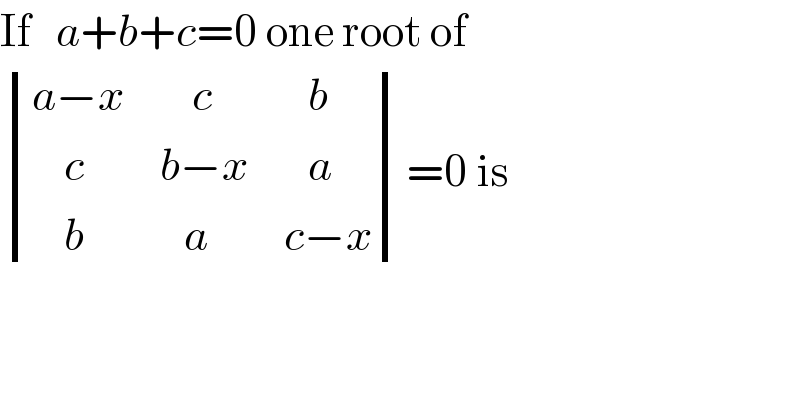
Answered by som(math1967) last updated on 10/Aug/20
![determinant (((a+b+c−x),(a+b+c−x),(a+b+c−x)),(c,(b−x),a),(b,a,(c−x)))=0 [R_1 ^′ →R_1 +R_2 +R_3 ] (a+b+c−x) determinant ((1,1,1),(c,(b−x),a),(b,(a ),(c−x)))=0 (a+b+c−x) determinant ((0,0,1),((c−b+x),(b−x−a),a),((b−a),(a−c+x),(c−x)))=0★ (a+b+c−x) determinant (((c−b+x),(b−x−a)),((b−a),(a−c+x)))=0 (a+b+c−x)(x^2 −a^2 −b^2 −c^2 +ab+bc+ca)=0 ⇒x=(a+b+c)=0 x=±(√(a^2 +b^2 +c^2 −ab−bc−ca)) ★C_1 ^′ →C_1 −C_2 C_2 ^′ →C_2 −C_3](Q107361.png)
Answered by 1549442205PVT last updated on 10/Aug/20
![We have determinant (((a−x),( c),( b)),(( c),(b−x),( a)),(( b),( a),(c−x)))=0 ⇔(a−x)(b−x)(c−x)+2abc−b^2 (b−x)−c^2 (c−x)−a^2 (a−x)=0 ⇔−x^3 +(a+b+c)x^2 +(a^2 +b^2 +c^2 −ab−bc−ca)x −(a^3 +b^3 +c^3 −2abc)+abc=0 ⇔x^3 −(a+b+c)x^2 −(a^2 +b^2 +c^2 −ab−bc−ca)x +(a^3 +b^3 +c^3 −3abc)=0(∗) Apply the identity a^3 +b^3 +c^3 −3abc=(a+b+c)(a^2 +b^2 +c^2 −ab−bc−ca)(1)we have (∗)⇔x^2 [x−(a+b+c)]−(a^2 +b^2 +c^2 −ab−bc−ca)x +(a+b+c)(a^2 +b^2 +c^2 −ab−bc−ca)=0 ⇔(∗)⇔x^2 [x−(a+b+c)]−[x−(a+b+c)](a^2 +b^2 +c^2 −ab−bc−ca)=0 ⇔[x−(a+b+c)].[x^2 −(a^2 +b^2 +c^2 −ab−bc−ca)]=0 This show that x=a+b+c is a root of the equation (∗)(q.e.d) In adition,we see that the given has two another real roots that are x=±(√(a^2 +b^2 +c^2 −ab−bc−ca)) .The under root expression is non−negative number since we have always a^2 +b^2 +c^2 −ab−bc−ca= (1/2)[(a−b)^2 +(b−c)^2 +(c−a)^2 ]≥0∀a,b,c∈R](Q107391.png)
| ||
Question and Answers Forum | ||
Question Number 107330 by saorey0202 last updated on 10/Aug/20 | ||
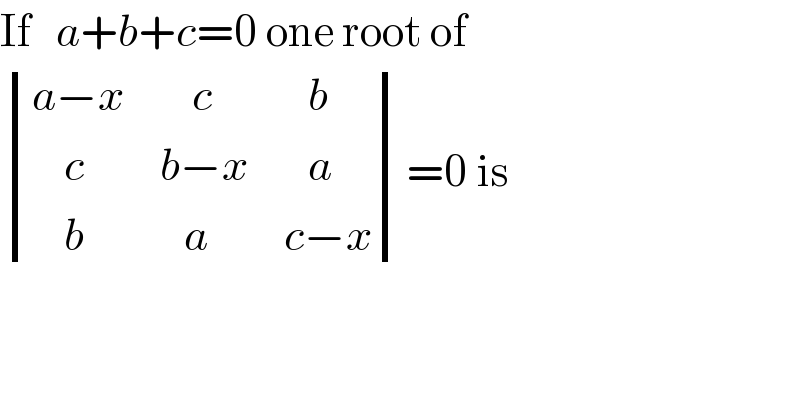 | ||
Answered by som(math1967) last updated on 10/Aug/20 | ||
![determinant (((a+b+c−x),(a+b+c−x),(a+b+c−x)),(c,(b−x),a),(b,a,(c−x)))=0 [R_1 ^′ →R_1 +R_2 +R_3 ] (a+b+c−x) determinant ((1,1,1),(c,(b−x),a),(b,(a ),(c−x)))=0 (a+b+c−x) determinant ((0,0,1),((c−b+x),(b−x−a),a),((b−a),(a−c+x),(c−x)))=0★ (a+b+c−x) determinant (((c−b+x),(b−x−a)),((b−a),(a−c+x)))=0 (a+b+c−x)(x^2 −a^2 −b^2 −c^2 +ab+bc+ca)=0 ⇒x=(a+b+c)=0 x=±(√(a^2 +b^2 +c^2 −ab−bc−ca)) ★C_1 ^′ →C_1 −C_2 C_2 ^′ →C_2 −C_3](Q107361.png) | ||
| ||
Answered by 1549442205PVT last updated on 10/Aug/20 | ||
![We have determinant (((a−x),( c),( b)),(( c),(b−x),( a)),(( b),( a),(c−x)))=0 ⇔(a−x)(b−x)(c−x)+2abc−b^2 (b−x)−c^2 (c−x)−a^2 (a−x)=0 ⇔−x^3 +(a+b+c)x^2 +(a^2 +b^2 +c^2 −ab−bc−ca)x −(a^3 +b^3 +c^3 −2abc)+abc=0 ⇔x^3 −(a+b+c)x^2 −(a^2 +b^2 +c^2 −ab−bc−ca)x +(a^3 +b^3 +c^3 −3abc)=0(∗) Apply the identity a^3 +b^3 +c^3 −3abc=(a+b+c)(a^2 +b^2 +c^2 −ab−bc−ca)(1)we have (∗)⇔x^2 [x−(a+b+c)]−(a^2 +b^2 +c^2 −ab−bc−ca)x +(a+b+c)(a^2 +b^2 +c^2 −ab−bc−ca)=0 ⇔(∗)⇔x^2 [x−(a+b+c)]−[x−(a+b+c)](a^2 +b^2 +c^2 −ab−bc−ca)=0 ⇔[x−(a+b+c)].[x^2 −(a^2 +b^2 +c^2 −ab−bc−ca)]=0 This show that x=a+b+c is a root of the equation (∗)(q.e.d) In adition,we see that the given has two another real roots that are x=±(√(a^2 +b^2 +c^2 −ab−bc−ca)) .The under root expression is non−negative number since we have always a^2 +b^2 +c^2 −ab−bc−ca= (1/2)[(a−b)^2 +(b−c)^2 +(c−a)^2 ]≥0∀a,b,c∈R](Q107391.png) | ||
| ||