
Question Number 107461 by Don08q last updated on 10/Aug/20

Commented by john santu last updated on 11/Aug/20
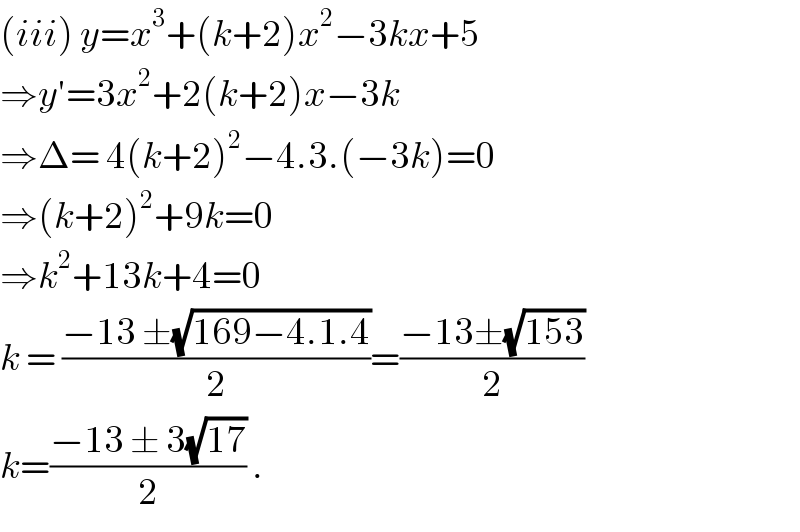
$$\left({iii}\right)\:{y}={x}^{\mathrm{3}} +\left({k}+\mathrm{2}\right){x}^{\mathrm{2}} −\mathrm{3}{kx}+\mathrm{5} \\ $$$$\Rightarrow{y}'=\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}\left({k}+\mathrm{2}\right){x}−\mathrm{3}{k} \\ $$$$\Rightarrow\Delta=\:\mathrm{4}\left({k}+\mathrm{2}\right)^{\mathrm{2}} −\mathrm{4}.\mathrm{3}.\left(−\mathrm{3}{k}\right)=\mathrm{0} \\ $$$$\Rightarrow\left({k}+\mathrm{2}\right)^{\mathrm{2}} +\mathrm{9}{k}=\mathrm{0} \\ $$$$\Rightarrow{k}^{\mathrm{2}} +\mathrm{13}{k}+\mathrm{4}=\mathrm{0}\: \\ $$$${k}\:=\:\frac{−\mathrm{13}\:\pm\sqrt{\mathrm{169}−\mathrm{4}.\mathrm{1}.\mathrm{4}}}{\mathrm{2}}=\frac{−\mathrm{13}\pm\sqrt{\mathrm{153}}}{\mathrm{2}} \\ $$$${k}=\frac{−\mathrm{13}\:\pm\:\mathrm{3}\sqrt{\mathrm{17}}}{\mathrm{2}}\:. \\ $$
Answered by john santu last updated on 11/Aug/20
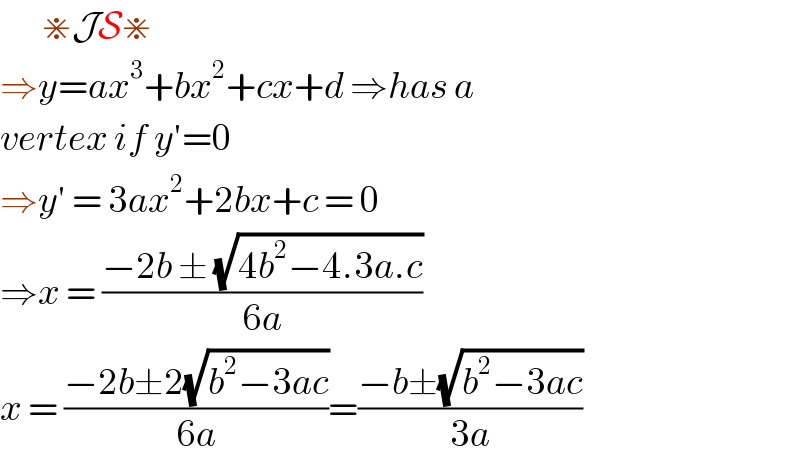
$$\:\:\:\:\:\:\:\divideontimes\mathcal{JS}\divideontimes \\ $$$$\Rightarrow{y}={ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{cx}+{d}\:\Rightarrow{has}\:{a} \\ $$$${vertex}\:{if}\:{y}'=\mathrm{0}\: \\ $$$$\Rightarrow{y}'\:=\:\mathrm{3}{ax}^{\mathrm{2}} +\mathrm{2}{bx}+{c}\:=\:\mathrm{0} \\ $$$$\Rightarrow{x}\:=\:\frac{−\mathrm{2}{b}\:\pm\:\sqrt{\mathrm{4}{b}^{\mathrm{2}} −\mathrm{4}.\mathrm{3}{a}.{c}}}{\mathrm{6}{a}} \\ $$$${x}\:=\:\frac{−\mathrm{2}{b}\pm\mathrm{2}\sqrt{{b}^{\mathrm{2}} −\mathrm{3}{ac}}}{\mathrm{6}{a}}=\frac{−{b}\pm\sqrt{{b}^{\mathrm{2}} −\mathrm{3}{ac}}}{\mathrm{3}{a}} \\ $$
Commented by john santu last updated on 11/Aug/20
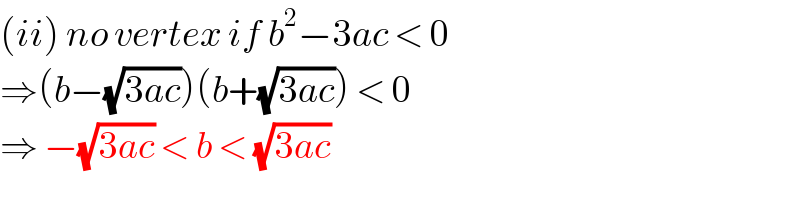
$$\left({ii}\right)\:{no}\:{vertex}\:{if}\:{b}^{\mathrm{2}} −\mathrm{3}{ac}\:<\:\mathrm{0} \\ $$$$\Rightarrow\left({b}−\sqrt{\mathrm{3}{ac}}\right)\left({b}+\sqrt{\mathrm{3}{ac}}\right)\:<\:\mathrm{0} \\ $$$$\Rightarrow\:−\sqrt{\mathrm{3}{ac}}\:<\:{b}\:<\:\sqrt{\mathrm{3}{ac}}\: \\ $$
Commented by Don08q last updated on 11/Aug/20

$${Thank}\:{you}\:{Sir} \\ $$
Answered by 1549442205PVT last updated on 11/Aug/20

$$\mathrm{We}\:\mathrm{need}\:\mathrm{to}\:\mathrm{have}\:\mathrm{the}\:\mathrm{hypothesis}\:\mathrm{that} \\ $$$$\mathrm{a},\mathrm{b}\neq\mathrm{0}.\mathrm{Then}\:\mathrm{denote}\:\mathrm{by}\:\mathrm{C}\:\mathrm{the}\:\mathrm{graph}\:\mathrm{of} \\ $$$$\mathrm{y}=\mathrm{ax}^{\mathrm{3}} +\mathrm{bx}^{\mathrm{2}} +\mathrm{cx}+\mathrm{d}.\mathrm{We}\:\mathrm{have} \\ $$$$\mathrm{y}'=\mathrm{3ax}^{\mathrm{2}} +\mathrm{2bx}+\mathrm{c}=\mathrm{0}\Leftrightarrow\mathrm{x}_{\mathrm{1},\mathrm{2}} =\frac{−\mathrm{b}\pm\sqrt{\mathrm{b}^{\mathrm{2}} −\mathrm{3ac}}}{\mathrm{3a}} \\ $$$$\mathrm{y}''=\mathrm{6ax}+\mathrm{2b}=\mathrm{0}\Leftrightarrow\mathrm{x}_{\mathrm{0}} =−\mathrm{b}/\mathrm{3a} \\ $$$$\left.\mathrm{i}\right)\mathrm{if}\:\Delta=\mathrm{b}^{\mathrm{2}} −\mathrm{3ac}>\mathrm{0}\:\mathrm{the}\:\mathrm{eqn}.\mathrm{y}'=\mathrm{0}\:\mathrm{has}\: \\ $$$$\mathrm{two}\:\mathrm{real}\:\mathrm{roots}\:\mathrm{and}\:\mathrm{y}'\:\mathrm{change}\:\mathrm{the}\:\mathrm{sign}\:\mathrm{when} \\ $$$$\mathrm{passes}\:\mathrm{through}\:\mathrm{its}\:\mathrm{roots}\:,\mathrm{so}\:\mathrm{the}\:\mathrm{curve} \\ $$$$\mathrm{C}\:\mathrm{has}\:\mathrm{two}\:\:\mathrm{extremums}\:\mathrm{points}\left(\mathrm{vertexes}\right) \\ $$$$\left.\mathrm{ii}\right)\mathrm{If}\:\mathrm{b}^{\mathrm{2}} −\mathrm{3ac}=\mathrm{0}\:\mathrm{then}\:\mathrm{x}_{\mathrm{0}} =\mathrm{x}_{\mathrm{1}} =\mathrm{x}_{\mathrm{2}} =−\mathrm{b}/\mathrm{3a}. \\ $$$$\mathrm{Then}\:\mathrm{the}\:\:\mathrm{given}\:\mathrm{function}\:\mathrm{has}\:\mathrm{no}\:\:\mathrm{extremum} \\ $$$$\left(\mathrm{vertex}\right)\:\mathrm{because}\:\mathrm{y}'\mathrm{don}'\mathrm{t}\:\mathrm{change}\:\mathrm{the} \\ $$$$\mathrm{sign}\:\mathrm{when}\:\mathrm{go}\:\mathrm{through}\:\mathrm{x}_{\mathrm{0}} .\mathrm{Hence},\mathrm{the} \\ $$$$\mathrm{condition}\:\mathrm{need}\:\mathrm{and}\:\mathrm{enough}\:\mathrm{for}\:\mathrm{the}\:\mathrm{curve} \\ $$$$\mathrm{of}\:\mathrm{degree}\:\mathrm{3}\:\mathrm{has}\:\mathrm{a}\:\mathrm{saddle}\:\mathrm{point}\:\mathrm{be}\: \\ $$$$\Delta=\mathrm{b}^{\mathrm{2}} −\mathrm{3ac}=\mathrm{0} \\ $$$$\left.\mathrm{iii}\right)\mathrm{The}\:\mathrm{curve}\:\mathrm{y}=\mathrm{x}^{\mathrm{3}} +\left(\mathrm{k}+\mathrm{2}\right)\mathrm{x}^{\mathrm{2}} −\mathrm{3kx}+\mathrm{5}\left(\mathrm{C}_{\mathrm{k}} \right) \\ $$$$\mathrm{has}\:\mathrm{the}\:\mathrm{saddle}\:\mathrm{point}\:\mathrm{if}\:\mathrm{and}\:\mathrm{only}\:\mathrm{if}\: \\ $$$$\mathrm{y}'=\mathrm{3x}^{\mathrm{2}} +\mathrm{2}\left(\mathrm{k}+\mathrm{2}\right)\mathrm{x}−\mathrm{3k}=\mathrm{0}\:\mathrm{has}\:\mathrm{unique}\:\mathrm{root} \\ $$$$\Leftrightarrow\Delta'=\left(\mathrm{k}+\mathrm{2}\right)^{\mathrm{2}} +\mathrm{9k}=\mathrm{0}\Leftrightarrow\mathrm{k}^{\mathrm{2}} +\mathrm{13k}+\mathrm{4}=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{k}_{\mathrm{1},\mathrm{2}} =\frac{−\mathrm{13}\pm\mathrm{3}\sqrt{\mathrm{17}}}{\mathrm{2}}.\mathrm{Then}\:\mathrm{x}_{\mathrm{0}} =\frac{−\left(\mathrm{k}+\mathrm{2}\right)}{\mathrm{3}} \\ $$$$\left.+\right)\mathrm{for}\:\mathrm{k}_{\mathrm{1}} =\frac{−\mathrm{13}+\mathrm{3}\sqrt{\mathrm{17}}}{\mathrm{2}}\Rightarrow\mathrm{x}_{\mathrm{0}} =−\frac{−\mathrm{9}+\mathrm{3}\sqrt{\mathrm{17}}}{\mathrm{6}} \\ $$$$\left.+\right)\mathrm{For}\:\mathrm{k}_{\mathrm{2}} =\frac{−\mathrm{13}−\mathrm{3}\sqrt{\mathrm{17}}}{\mathrm{2}}\Rightarrow\mathrm{x}_{\mathrm{0}} =\frac{\mathrm{9}+\mathrm{3}\sqrt{\mathrm{17}}}{\mathrm{6}} \\ $$$$\mathrm{Thus},\mathrm{C}_{\mathrm{k}} \:\mathrm{has}\:\mathrm{the}\:\mathrm{saddle}\:\mathrm{point}\:\mathrm{if}\:\mathrm{and}\: \\ $$$$\mathrm{only}\:\mathrm{if}\:\mathrm{k}=\frac{−\mathrm{13}\pm\mathrm{3}\sqrt{\mathrm{17}}}{\mathrm{2}} \\ $$
Commented by Don08q last updated on 11/Aug/20
$${Comprehensive}\:{explanation}.\:{Thank}\:{you} \\ $$
