
Question and Answers Forum
Question Number 107483 by john santu last updated on 11/Aug/20
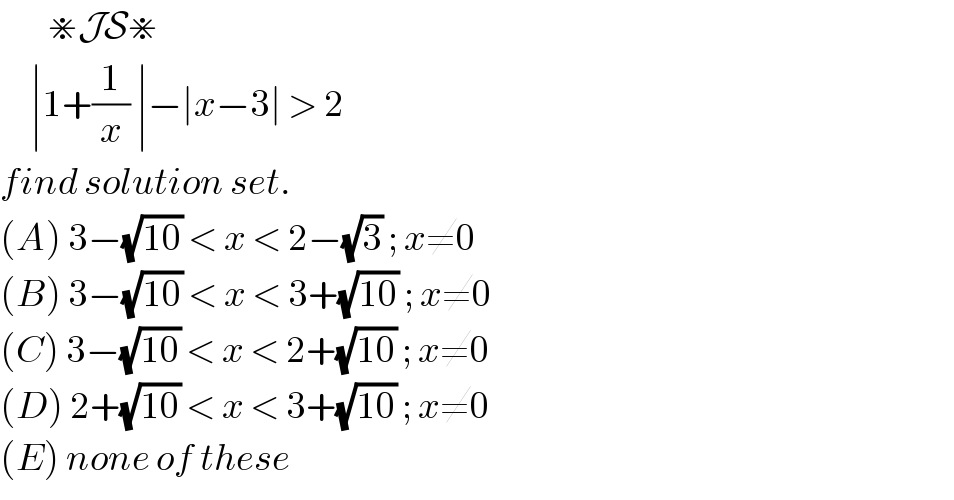
Answered by Her_Majesty last updated on 11/Aug/20
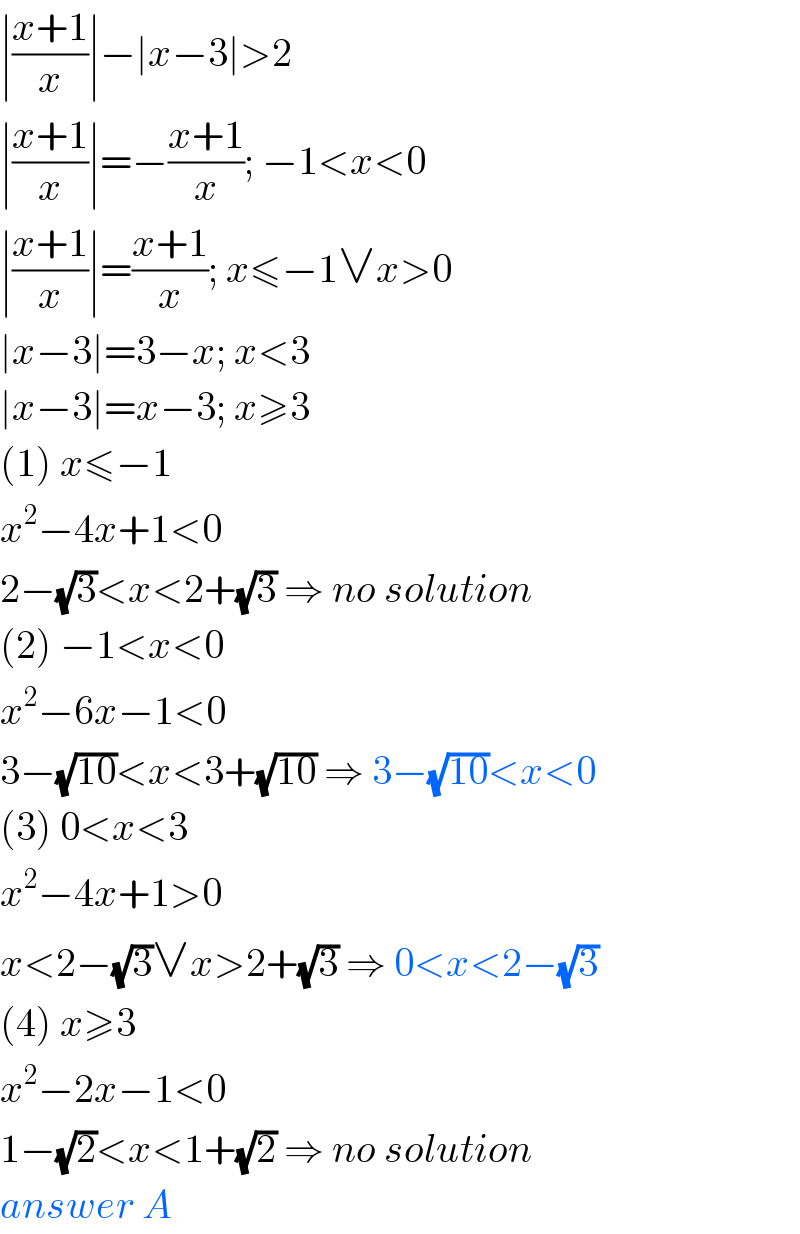
Commented bybemath last updated on 11/Aug/20
sorry to ask. are you MJS sir?
Commented byDwaipayan Shikari last updated on 11/Aug/20
I also think��
Commented byHer_Majesty last updated on 11/Aug/20
Commented byAr Brandon last updated on 11/Aug/20
It 's evident guys.�� I noticed it eversince but didn't want to raise an alarm. ��Mr MJS stopped participating in the forum's discussion after a little dispute with Mr Thorendsen who decided not to take part any longer. ��And after sometime Her majesty came into play. That was from the 1st of this month. I recognized him through his ways of solving problems. There are some symbols which only Mr MJS uses. And through his expressions. I received my confirmation when he tried to convince me that he was a lady.�� That was really weird. Most girls I know are so shy to take part in maths discussions, like the ones in my whatsapp school group. And I once had to also desguise myself using a female account, then sent solutions to exercises using two different accounts.���� I knew Mr MJS wasn't just gonna give up on this forum like that.��
Commented byAr Brandon last updated on 11/Aug/20
I wish Mr Thorendsen also comes back. He's been of great help just for the little while he's been here.����
Commented by$@y@m last updated on 11/Aug/20
I think all such discussion are meaningless. This forum, like mathematics, is absolutely abstract. Irrespective of your efforts, you can't make it concrete. It's human nature to have curiosity to know who is on other side answering questions. Let them be in disguise who wants to be. Just get benefited from their knowledge, thank them and enjoy the wonderful app. ������
Commented byAr Brandon last updated on 11/Aug/20
������ Alright Sir. Just some fun.��
Commented bybemath last updated on 11/Aug/20
my inner eyes say that you are sir MJS
Commented bySarah85 last updated on 11/Aug/20
I'm a "girl" aged 35 and I'm still on this forum. I used a different nick name earlier, forgot my login... both the level of questions and the quality of discussions went down lately, maybe a reason to leave for some people.
Commented byHer_Majesty last updated on 11/Aug/20

Commented bySarah85 last updated on 11/Aug/20
Mr Santu I'm sorry my words were ambiguous. I meant questions like "1+1=??? Who is able to solve this?" and on the other hand "integrate x^x^x^..." I hope it's clear now what I'm talking about.
Commented byjohn santu last updated on 11/Aug/20

Commented byAr Brandon last updated on 11/Aug/20
��Hi Sarah. Nice to learn about the existence of active females like you on this plate-forme. And you're >2×(my age).��
Commented byAr Brandon last updated on 11/Aug/20
You're funny Sir.���� Dark twin of Queen Elizabeth.�� Greetings your majesty.����
Commented byAr Brandon last updated on 11/Aug/20
Maths is fun�� Sir John. No need to be so tensed or so serious at the level of getting stressed up.��
Answered by 1549442205PVT last updated on 11/Aug/20

