Question Number 107498 by Ar Brandon last updated on 11/Aug/20
$$\mathrm{Show}\:\mathrm{that}\: \\ $$$$\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\prod}}\left(\mathrm{a}−\mathrm{e}^{\frac{\mathrm{2}{i}\mathrm{k}\pi}{\mathrm{n}}} \right)\left(\mathrm{a}−\mathrm{e}^{−\frac{\mathrm{2}{i}\mathrm{k}\pi}{\mathrm{n}}} \right)=\left(\mathrm{a}^{\mathrm{n}} −\mathrm{1}\right)^{\mathrm{2}} \\ $$
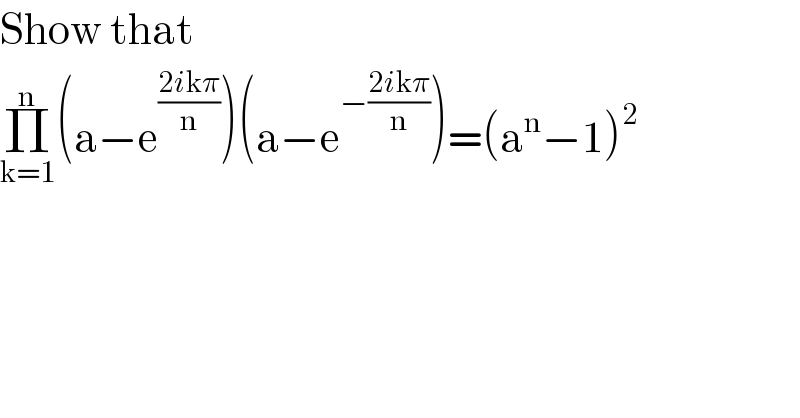
Answered by 1549442205PVT last updated on 11/Aug/20
![Consider the equation of degree n: x^n −1=0(∗)⇔x^n =1⇔x=^n (√1) =(cos2kπ+isin2kπ)^(1/n) =cos((2kπ)/n)+isin((2kπ)/n) for k=1,2,...,n.Thus,the equation (∗) has n roots which each of them be a n−th root of unit .We denote the that roots to be δ_1 ,δ_2 ,...,δ_n .In addition,we see that α_k =cos((2kπ)/n)−isin((2kπ)/n)(k=1..n^(−) ) are also n different n−th roots of unit but α_i and δ_i are two conjugate number together means α_i δ_i =1and so we have δ_1 .δ_2 ....δ_n =α_1 .α_2 ....α_n =1.Then we have Π_(k=1) ^n (a−e^((2kπi)/n) )(a−e^((−2kπi)/n) ),(e^((2kπi)/n) =cos((2kπ)/n)+isin((2kπ)/n),(e^((−2kπi)/n) =cos((2kπ)/n)−isin((2kπ)/n)) =Π_(k=1) ^(n) (a−δ_k )(a−α_k )=Π_(k=1) ^(n) (a−δ_k )Π_(k=1) ^(n) (a−α_k ) =[a^n −a^(n−1) (Σ_(k=1) ^(n) δ_k )+a^(n−2) (Σ_(i≠j) δ_i δ_j )−...+aΣ_(i_1 ≠i_2 ≠...≠i_(n−1) ) (δ_i_1 δ_i_2 ...δ_i_(n−1) )−δ_1 δ_2 ..δ_n ] =(a^n −1)(becau se δ_k (k=1...n^(−) )be n roots of the equation:x^n −1=0,so all sums of form Σδ_k ,Σδ_i δ_j ,....Σ(δ_i_1 δ_i_2 ...δ_i_(n−1) ) equal to zero−Vieta′s theorem) Similarly,we have Π_(k=1) ^n (a−α_k )=(a^n −1) Consequently,Π_(k=1) ^n (a−e^((2kπi)/n) )(a−e^((−2kπi)/n) ) =(a^n −1)^2 (q.e.d)](Q107539.png)
$$\mathrm{Consider}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{degree}\:\mathrm{n}: \\ $$$$\mathrm{x}^{\mathrm{n}} −\mathrm{1}=\mathrm{0}\left(\ast\right)\Leftrightarrow\mathrm{x}^{\mathrm{n}} =\mathrm{1}\Leftrightarrow\mathrm{x}=\:^{\mathrm{n}} \sqrt{\mathrm{1}}\: \\ $$$$=\left(\mathrm{cos2k}\pi+\mathrm{isin2k}\pi\right)^{\frac{\mathrm{1}}{\mathrm{n}}} =\mathrm{cos}\frac{\mathrm{2k}\pi}{\mathrm{n}}+\mathrm{isin}\frac{\mathrm{2k}\pi}{\mathrm{n}} \\ $$$$\mathrm{for}\:\mathrm{k}=\mathrm{1},\mathrm{2},...,\mathrm{n}.\mathrm{Thus},\mathrm{the}\:\mathrm{equation}\:\left(\ast\right) \\ $$$$\mathrm{has}\:\mathrm{n}\:\mathrm{roots}\:\mathrm{which}\:\mathrm{each}\:\mathrm{of}\:\mathrm{them}\:\mathrm{be}\:\mathrm{a} \\ $$$$\mathrm{n}−\mathrm{th}\:\mathrm{root}\:\mathrm{of}\:\mathrm{unit}\:.\mathrm{We}\:\mathrm{denote}\:\mathrm{the}\:\mathrm{that} \\ $$$$\mathrm{roots}\:\mathrm{to}\:\mathrm{be}\:\delta_{\mathrm{1}} ,\delta_{\mathrm{2}} ,...,\delta_{\mathrm{n}} .\mathrm{In}\:\mathrm{addition},\mathrm{we} \\ $$$$\mathrm{see}\:\mathrm{that}\:\:\:\:\alpha_{\mathrm{k}} =\mathrm{cos}\frac{\mathrm{2k}\pi}{\mathrm{n}}−\mathrm{isin}\frac{\mathrm{2k}\pi}{\mathrm{n}}\left(\mathrm{k}=\overline {\mathrm{1}..\mathrm{n}}\right) \\ $$$$\mathrm{are}\:\mathrm{also}\:\mathrm{n}\:\mathrm{different}\:\:\mathrm{n}−\mathrm{th}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{unit} \\ $$$$\mathrm{but}\:\alpha_{\mathrm{i}} \mathrm{and}\:\delta_{\mathrm{i}} \mathrm{are}\:\mathrm{two}\:\mathrm{conjugate}\:\mathrm{number} \\ $$$$\mathrm{together}\:\mathrm{means}\:\alpha_{\mathrm{i}} \delta_{\mathrm{i}} =\mathrm{1and}\:\mathrm{so}\:\mathrm{we}\:\mathrm{have} \\ $$$$\delta_{\mathrm{1}} .\delta_{\mathrm{2}} ....\delta_{\mathrm{n}} =\alpha_{\mathrm{1}} .\alpha_{\mathrm{2}} ....\alpha_{\mathrm{n}} =\mathrm{1}.\mathrm{Then}\:\mathrm{we}\:\mathrm{have} \\ $$$$\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\prod}}\left(\mathrm{a}−\mathrm{e}^{\frac{\mathrm{2k}\pi\mathrm{i}}{\mathrm{n}}} \right)\left(\mathrm{a}−\mathrm{e}^{\frac{−\mathrm{2k}\pi\mathrm{i}}{\mathrm{n}}} \right),\left(\mathrm{e}^{\frac{\mathrm{2k}\pi\mathrm{i}}{\mathrm{n}}} =\mathrm{cos}\frac{\mathrm{2k}\pi}{\mathrm{n}}+\mathrm{isin}\frac{\mathrm{2k}\pi}{\mathrm{n}},\left(\mathrm{e}^{\frac{−\mathrm{2k}\pi\mathrm{i}}{\mathrm{n}}} =\mathrm{cos}\frac{\mathrm{2k}\pi}{\mathrm{n}}−\mathrm{isin}\frac{\mathrm{2k}\pi}{\mathrm{n}}\right)\right. \\ $$$$=\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\Pi}}\left(\mathrm{a}−\delta_{\mathrm{k}} \right)\left(\mathrm{a}−\alpha_{\mathrm{k}} \right)=\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\Pi}}\left(\mathrm{a}−\delta_{\mathrm{k}} \right)\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\Pi}}\left(\mathrm{a}−\alpha_{\mathrm{k}} \right) \\ $$$$=\left[\mathrm{a}^{\mathrm{n}} −\mathrm{a}^{\mathrm{n}−\mathrm{1}} \left(\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\Sigma}}\delta_{\mathrm{k}} \right)+\mathrm{a}^{\mathrm{n}−\mathrm{2}} \left(\underset{\mathrm{i}\neq\mathrm{j}} {\Sigma}\delta_{\mathrm{i}} \delta_{\mathrm{j}} \right)−...+\mathrm{a}\underset{\mathrm{i}_{\mathrm{1}} \neq\mathrm{i}_{\mathrm{2}} \neq...\neq\mathrm{i}_{\mathrm{n}−\mathrm{1}} } {\Sigma}\left(\delta_{\mathrm{i}_{\mathrm{1}} } \delta_{\mathrm{i}_{\mathrm{2}} } ...\delta_{\mathrm{i}_{\mathrm{n}−\mathrm{1}} } \right)−\delta_{\mathrm{1}} \delta_{\mathrm{2}} ..\delta_{\mathrm{n}} \right] \\ $$$$=\left(\mathrm{a}^{\mathrm{n}} −\mathrm{1}\right)\left(\mathrm{becau}\:\mathrm{se}\:\delta_{\mathrm{k}} \left(\mathrm{k}=\overline {\mathrm{1}...\mathrm{n}}\right)\mathrm{be}\:\mathrm{n}\right. \\ $$$$\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation}:\mathrm{x}^{\mathrm{n}} −\mathrm{1}=\mathrm{0},\mathrm{so}\:\mathrm{all} \\ $$$$\mathrm{sums}\:\mathrm{of}\:\mathrm{form}\:\Sigma\delta_{\mathrm{k}} ,\Sigma\delta_{\mathrm{i}} \delta_{\mathrm{j}} ,....\Sigma\left(\delta_{\mathrm{i}_{\mathrm{1}} } \delta_{\mathrm{i}_{\mathrm{2}} } ...\delta_{\mathrm{i}_{\mathrm{n}−\mathrm{1}} } \right) \\ $$$$\left.\mathrm{equal}\:\mathrm{to}\:\mathrm{zero}−\mathrm{Vieta}'\mathrm{s}\:\mathrm{theorem}\right) \\ $$$$\mathrm{Similarly},\mathrm{we}\:\mathrm{have} \\ $$$$\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\prod}}\left(\mathrm{a}−\alpha_{\mathrm{k}} \right)=\left(\mathrm{a}^{\mathrm{n}} −\mathrm{1}\right) \\ $$$$\mathrm{Consequently},\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\prod}}\left(\mathrm{a}−\mathrm{e}^{\frac{\mathrm{2k}\pi\mathrm{i}}{\mathrm{n}}} \right)\left(\mathrm{a}−\mathrm{e}^{\frac{−\mathrm{2k}\pi\mathrm{i}}{\mathrm{n}}} \right) \\ $$$$=\left(\mathrm{a}^{\mathrm{n}} −\mathrm{1}\right)^{\mathrm{2}} \left(\boldsymbol{\mathrm{q}}.\boldsymbol{\mathrm{e}}.\boldsymbol{\mathrm{d}}\right)\: \\ $$
Commented by Ar Brandon last updated on 11/Aug/20
Thanks so very much Sir �� May I write you in case of any difficulties.��
Commented by 1549442205PVT last updated on 13/Aug/20
$$\mathrm{Thank}\:\mathrm{you},\mathrm{but}\:\mathrm{only}\:\:\mathrm{in}\:\mathrm{public}\:\mathrm{situation} \\ $$$$,\mathrm{Sir} \\ $$