Question and Answers Forum

All Questions      Topic List

Matrices and Determinants Questions

Previous in All Question      Next in All Question      

Previous in Matrices and Determinants      Next in Matrices and Determinants      

Question Number 107547 by hgrocks last updated on 11/Aug/20

Commented by hgrocks last updated on 11/Aug/20

Can anyone solve this Q without using eigen values

Commented by bemath last updated on 11/Aug/20

$$tr\left(M\right)=trace\left(M\right)?$$

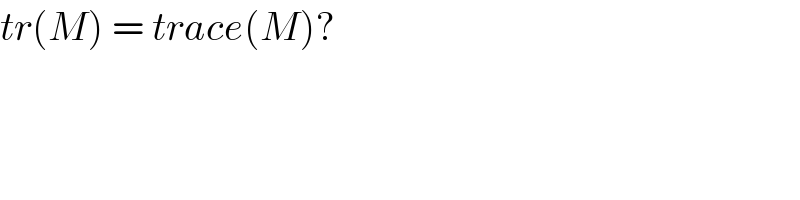
Commented by hgrocks last updated on 11/Aug/20

Yes it is trace of M

Commented by hgrocks last updated on 11/Aug/20

$$\mathrm{Pls}\mathrm{Solve}\mathrm{This}\mathrm{Q}$$

Commented by hgrocks last updated on 11/Aug/20

$$\mathrm{Anyone}?$$$$$$$$$$

Commented by mathmax by abdo last updated on 11/Aug/20

$$\mathrm{sir}\mathrm{dont}\mathrm{beg}\mathrm{the}\mathrm{answer}\mathrm{if}\mathrm{someone}\mathrm{have}\mathrm{a}\mathrm{idea}\mathrm{he}\mathrm{give}\mathrm{it}...$$

Answered by mathmax by abdo last updated on 12/Aug/20

$$\mathrm{let}\mathrm{take}\mathrm{a}\mathrm{try}\mathrm{with}\mathrm{this}\mathrm{limit}\mathrm{let}{\mathrm{A}}_{\mathrm{n}}=\left(\begin{array}{c}1\frac{\mathrm{x}}{\mathrm{n}}\\ -\frac{\mathrm{x}}{\mathrm{n}}1\end{array}\right)$$$$\mathrm{we}\mathrm{have}{\mathrm{A}}_{\mathrm{n}}=\sqrt{1+\frac{{\mathrm{x}}^2}{{\mathrm{n}}^2}}\times \left(\begin{array}{c}\frac{1}{\sqrt{1+\frac{{\mathrm{x}}^2}{{\mathrm{n}}^2}}}\frac{\mathrm{x}}{\mathrm{n}\sqrt{1+\frac{{\mathrm{x}}^2}{{\mathrm{n}}^2}}}\\ -\frac{\mathrm{x}}{\mathrm{n}\sqrt{1+\frac{{\mathrm{x}}^2}{{\mathrm{n}}^2}}}\frac{1}{\sqrt{1+\frac{{\mathrm{x}}^2}{{\mathrm{n}}^2}}}\end{array}\right)$$$$\mathrm{let}{\alpha }_{\mathrm{n}}\left(\mathrm{x}\right)=\sqrt{1+\frac{{\mathrm{x}}^2}{{\mathrm{n}}^2}}\Rightarrow {\mathrm{A}}_{\mathrm{n}}={\alpha }_{\mathrm{n}}\left(\mathrm{x}\right)\left(\begin{array}{c}\frac{1}{{\alpha }_{\mathrm{n}}\left(\mathrm{x}\right)}\frac{\mathrm{x}}{\mathrm{n}{\alpha }_{\mathrm{n}}\left(\mathrm{x}\right)}\\ -\frac{\mathrm{x}}{\mathrm{n}{\alpha }_{\mathrm{n}}\left(\mathrm{x}\right)}\frac{1}{{\alpha }_{\mathrm{n}}\left(\mathrm{x}\right)}\end{array}\right)$$$$\mathrm{we}\mathrm{have}\det \left(\begin{array}{c}......\\ \end{array}\right)=\frac{1}{{\alpha }_{\mathrm{n}}^2\left(\mathrm{x}\right)}+\frac{{\mathrm{x}}^2}{{\mathrm{n}}^2{\alpha }_{\mathrm{n}}^2\left(\mathrm{x}\right)}=\frac{1}{1+\frac{{\mathrm{x}}^2}{{\mathrm{n}}^2}}+\frac{{\mathrm{x}}^2}{{\mathrm{n}}^2(1+\frac{{\mathrm{x}}^2}{{\mathrm{n}}^2})}$$$$=\frac{{\mathrm{n}}^2}{{\mathrm{n}}^2+{\mathrm{x}}^2}+\frac{{\mathrm{x}}^2}{{\mathrm{n}}^2+{\mathrm{x}}^2}=1\mathrm{let}\frac{1}{{\alpha }_{\mathrm{n}}\left(\mathrm{x}\right)}=\cos \alpha \mathrm{and}\frac{\mathrm{x}}{\mathrm{n}{\alpha }_{\mathrm{n}}\left(\mathrm{x}\right)}=\sin \left(\alpha \right)\Rightarrow$$$$\tan \alpha =\frac{\mathrm{x}}{\mathrm{n}}\Rightarrow \alpha =\arctan \left(\frac{\mathrm{x}}{\mathrm{n}}\right)\Rightarrow$$$${{\mathrm{A}}_{\mathrm{n}}^{\frac{\mathrm{n}}{\mathrm{x}}}={\alpha }_{\mathrm{n}}\left(\mathrm{x}\right))}^{\frac{\mathrm{n}}{\mathrm{x}}}\times {\left(\begin{array}{c}\cos \alpha \sin \alpha \\ -\sin \alpha \cos \alpha \end{array}\right)}^{\frac{\mathrm{n}}{\mathrm{x}}}$$$$={(1+\frac{{\mathrm{x}}^2}{{\mathrm{n}}^2})}^{\frac{\mathrm{n}}{2\mathrm{x}}}\times {\left(\begin{array}{c}\cos \alpha \sin \alpha \\ -\sin \alpha \cos \alpha \end{array}\right)}^{\frac{\mathrm{n}}{\mathrm{x}}}\mathrm{if}\mathrm{x}\mathrm{divide}\mathrm{n}\mathrm{we}\mathrm{get}$$$${\mathrm{A}}_{\mathrm{n}}^{\frac{\mathrm{n}}{\mathrm{x}}}={(1+\frac{{\mathrm{x}}^2}{{\mathrm{n}}^2})}^{\frac{\mathrm{n}}{2\mathrm{x}}}\left(\begin{array}{c}\cos \left(\frac{\mathrm{n}}{\mathrm{x}}\arctan \left(\frac{\mathrm{x}}{\mathrm{n}}\right)\right)\sin \left(\frac{\mathrm{n}}{\mathrm{x}}\arctan \left(\frac{\mathrm{x}}{\mathrm{n}}\right)\right)\\ -\sin \left(\frac{\mathrm{n}}{\mathrm{x}}\arctan \left(\frac{\mathrm{x}}{\mathrm{n}}\right)\right)\cos \left(\frac{\mathrm{n}}{\mathrm{x}}\arctan \left(\frac{\mathrm{x}}{\mathrm{n}}\right)\right)\end{array}\right)$$$${(1+\frac{{\mathrm{x}}^2}{{\mathrm{n}}^2})}^{\frac{\mathrm{n}}{2\mathrm{x}}}={\mathrm{e}}^{\frac{\mathrm{n}}{2\mathrm{x}}\ln (1+\frac{{\mathrm{x}}^2}{{\mathrm{n}}^2})}\sim {\mathrm{e}}^{\frac{\mathrm{n}}{2\mathrm{x}}\left(\frac{{\mathrm{x}}^2}{{\mathrm{n}}^2}\right)}={\mathrm{e}}^{\frac{\mathrm{x}}{2\mathrm{n}}}\to 1\mathrm{also}\frac{\mathrm{n}}{\mathrm{x}}\arctan \left(\frac{\mathrm{x}}{\mathrm{n}}\right)$$$$\sim \frac{\mathrm{n}}{\mathrm{x}}.\frac{\mathrm{x}}{\mathrm{n}}=1\Rightarrow {\lim }_{\mathrm{n}\to +\mathrm{\infty }}{\mathrm{A}}_{\mathrm{n}}^{\frac{\mathrm{n}}{\mathrm{x}}}=\left(\begin{array}{c}\cos \left(1\right)\sin \left(1\right)\\ -\sin \left(1\right)\cos \left(1\right)\end{array}\right)$$$$\mathrm{and}\mathrm{Tr}\left({\lim }_{\mathrm{n}\to +\mathrm{\infty }}{\mathrm{A}}_{\mathrm{n}}^{\frac{\mathrm{n}}{\mathrm{x}}}\right)=2\cos \left(1\right)$$$$\mathrm{if}\mathrm{n}\mathrm{integr}\mathrm{and}\mathrm{x}\mathrm{dont}\mathrm{divide}\mathrm{n}\mathrm{n}=\mathrm{qx}+\mathrm{p}\mathrm{with}0<\mathrm{p}<\mathrm{x}$$$$\mathrm{be}\mathrm{continued}...$$$$$$$$$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com