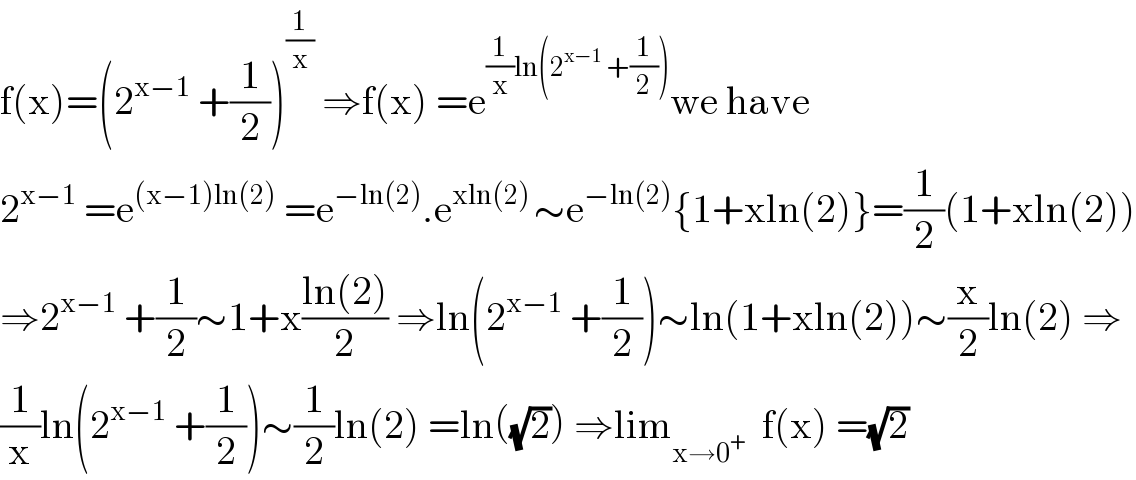L=lim_(x→0) (2^(x−1) +(1/2))^(1/x) = ?


Question and Answers Forum

All Questions Topic List
Limits Questions
Previous in All Question Next in All Question
Previous in Limits Next in Limits
Question Number 107550 by ajfour last updated on 11/Aug/20

$L = \lim_{x \to 0} {(2^{x - 1} + \frac{1}{2})}^{1 / x} = ?$
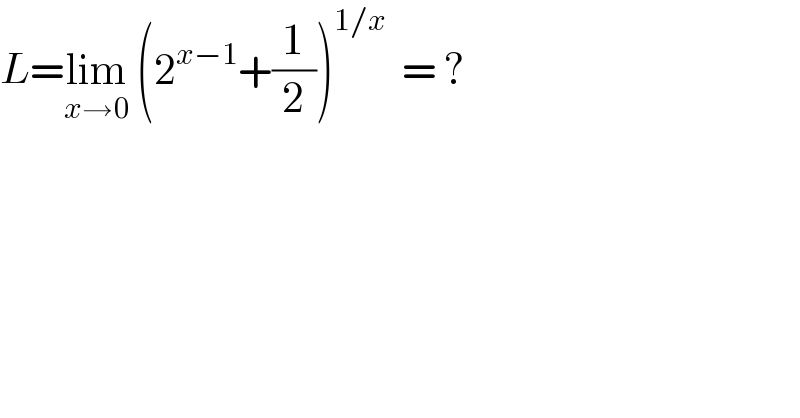
	Answered by hgrocks last updated on 11/Aug/20

	Commented by ajfour last updated on 11/Aug/20

	$G o o d, t h a n k s S i r .$
	Answered by john santu last updated on 11/Aug/20

	$⋇ JS ⋇$ $L = \lim_{x \to 0} {(\frac{1}{2} . 2^{x} + \frac{1}{2})}^{\frac{1}{x}}$ $L = \lim_{x \to 0} {(2^{x - 1} (1 + \frac{1}{2^{x}}))}^{\frac{1}{x}}$ $\ln L = \lim_{x \to 0} \frac{\ln (2^{x - 1}) + \ln (1 + 2^{- x})}{x}$ $\ln L = \lim_{x \to 0} \frac{2^{x - 1} \ln (2)}{2^{x - 1}} - \frac{2^{- x} \ln (2)}{1 + 2^{- x}}$ $\ln L = \frac{\frac{1}{2} \ln (2)}{\frac{1}{2}} - \frac{\ln (2)}{2} = \frac{1}{2} \ln (2) = \ln (\sqrt{2})$ $L = \sqrt{2}$
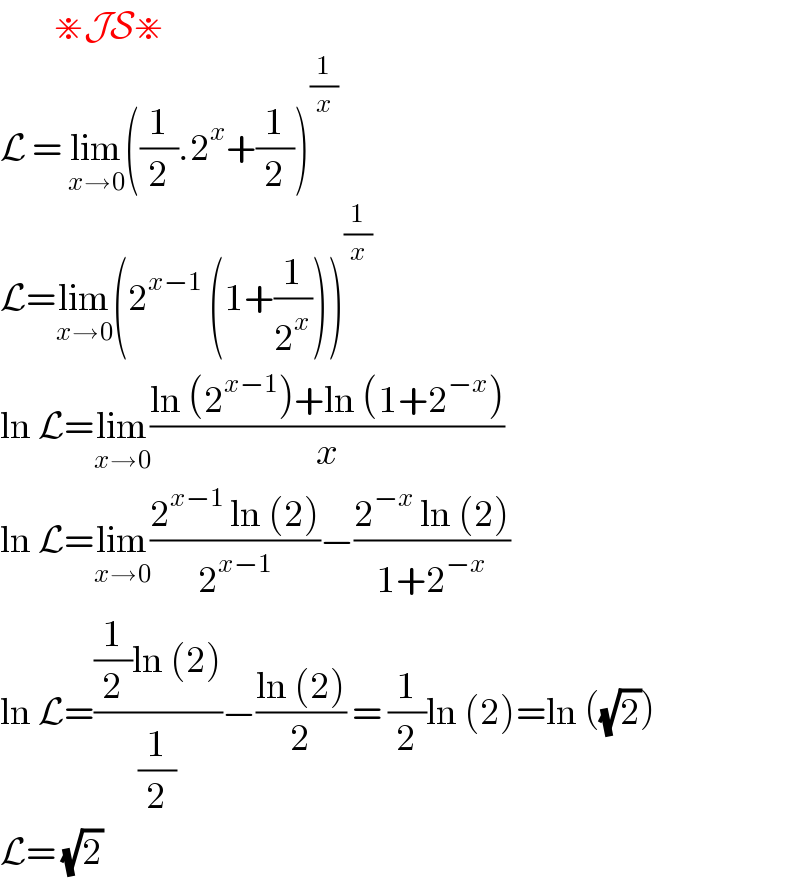
	Commented by ajfour last updated on 11/Aug/20

	$T h a n k s J S, b u t i t s e e m s b i t c u m b e r s o m e,$ $d o n t m i n d . .$
	Commented by john santu last updated on 11/Aug/20
	no problem. up to you
	Answered by Dwaipayan Shikari last updated on 11/Aug/20

	$\lim_{x \to 0} \frac{1}{x} l o g (1 + 2^{x - 1} - \frac{1}{2}) = l o g y$ $\frac{1}{x} . (2^{x - 1} - \frac{1}{2}) = l o g y$ $\frac{1}{2} . \frac{2^{x} - 1}{x} = l o g y$ $\frac{l o g (2)}{2} = l o g y$ $y = \sqrt{2}$
	Commented by ajfour last updated on 11/Aug/20

	$Q u i t e n i c e, t h a n k s!$
	Answered by ajfour last updated on 11/Aug/20
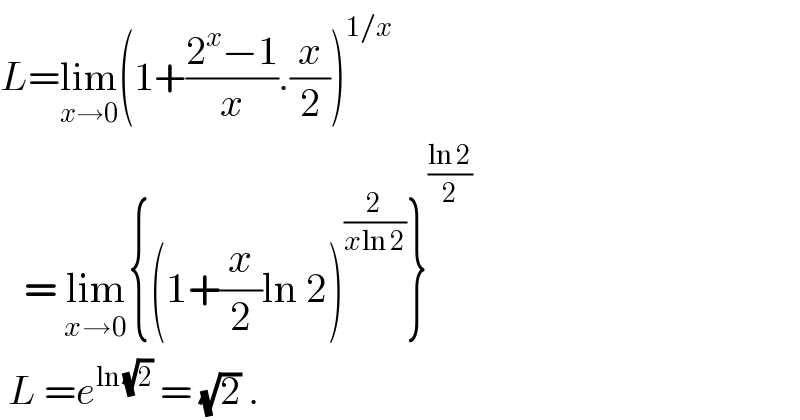
	$L=lim_(x→0) (1+((2^x −1)/x).(x/2))^(1/x) = lim_(x→0) {(1+(x/2)ln 2)^(2/(xln 2)) }^((ln 2)/2) L =e^(ln (√2)) = (√2) .$
	$L = \lim_{x \to 0} {(1 + \frac{2^{x} - 1}{x} . \frac{x}{2})}^{1 / x}$ $= \lim_{x \to 0} {{(1 + \frac{x}{2} \ln 2)}^{\frac{2}{x \ln 2}}}^{\frac{\ln 2}{2}}$ $L = e^{\ln \sqrt{2}} = \sqrt{2} .$
	Answered by mathmax by abdo last updated on 11/Aug/20
	$f(x)=(2^(x−1) +(1/2))^(1/x) ⇒f(x) =e^((1/x)ln(2^(x−1) +(1/2))) we have 2^(x−1) =e^((x−1)ln(2)) =e^(−ln(2)) .e^(xln(2) ) ∼e^(−ln(2)) {1+xln(2)}=(1/2)(1+xln(2)) ⇒2^(x−1) +(1/2)∼1+x((ln(2))/2) ⇒ln(2^(x−1) +(1/2))∼ln(1+xln(2))∼(x/2)ln(2) ⇒ (1/x)ln(2^(x−1) +(1/2))∼(1/2)ln(2) =ln((√2)) ⇒lim_(x→0^+ ) f(x) =(√2)$
	$f (x) = {(2^{x - 1} + \frac{1}{2})}^{\frac{1}{x}} \Rightarrow f (x) = e^{\frac{1}{x} \ln (2^{x - 1} + \frac{1}{2})} we have$ $2^{x - 1} = e^{(x - 1) \ln (2)} = e^{- \ln (2)} . e^{xln (2)} \sim e^{- \ln (2)} {1 + xln (2)} = \frac{1}{2} (1 + xln (2))$ $\Rightarrow 2^{x - 1} + \frac{1}{2} \sim 1 + x \frac{\ln (2)}{2} \Rightarrow \ln (2^{x - 1} + \frac{1}{2}) \sim \ln (1 + xln (2)) \sim \frac{x}{2} \ln (2) \Rightarrow$ $\frac{1}{x} \ln (2^{x - 1} + \frac{1}{2}) \sim \frac{1}{2} \ln (2) = \ln (\sqrt{2}) \Rightarrow \lim_{x \to 0^{+}} f (x) = \sqrt{2}$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum