Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 107706 by bemath last updated on 12/Aug/20

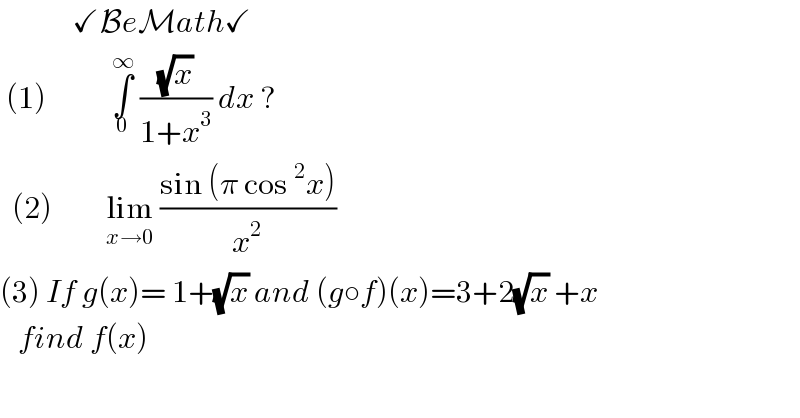
✓BeMath✓ (1) ∫_0 ^∞ ((√x)/(1+x^3 )) dx ? (2) lim_(x→0) ((sin (π cos^2 x))/x^2 ) (3) If g(x)= 1+(√x) and (g○f)(x)=3+2(√x) +x find f(x)

$$\:\:\:\:\:\:\:\:\:\:\:\:\checkmark\mathcal{B}{e}\mathcal{M}{ath}\checkmark \\ $$$$\:\left(\mathrm{1}\right)\:\:\:\:\:\:\:\:\:\:\:\underset{\mathrm{0}} {\overset{\infty} {\int}}\:\frac{\sqrt{{x}}}{\mathrm{1}+{x}^{\mathrm{3}} }\:{dx}\:? \\ $$$$\:\:\left(\mathrm{2}\right)\:\:\:\:\:\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\left(\pi\:\mathrm{cos}\:^{\mathrm{2}} {x}\right)}{{x}^{\mathrm{2}} }\: \\ $$$$\left(\mathrm{3}\right)\:{If}\:{g}\left({x}\right)=\:\mathrm{1}+\sqrt{{x}}\:{and}\:\left({g}\circ{f}\right)\left({x}\right)=\mathrm{3}+\mathrm{2}\sqrt{{x}}\:+{x} \\ $$$$\:\:\:{find}\:{f}\left({x}\right) \\ $$

Answered by bemath last updated on 12/Aug/20

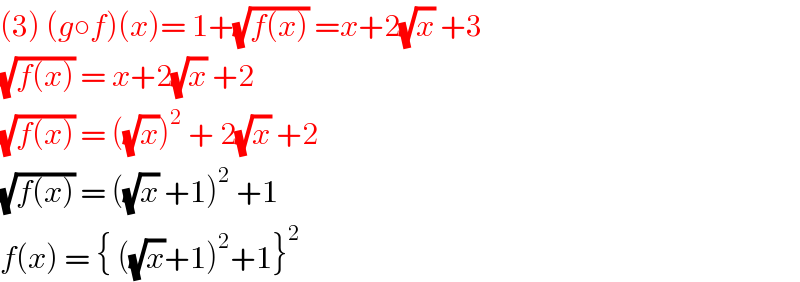
(3) (g○f)(x)= 1+(√(f(x))) =x+2(√x) +3 (√(f(x))) = x+2(√x) +2 (√(f(x))) = ((√x))^2 + 2(√x) +2 (√(f(x))) = ((√x) +1)^2 +1 f(x) = { ((√x)+1)^2 +1}^2

$$\left(\mathrm{3}\right)\:\left({g}\circ{f}\right)\left({x}\right)=\:\mathrm{1}+\sqrt{{f}\left({x}\right)}\:={x}+\mathrm{2}\sqrt{{x}}\:+\mathrm{3} \\ $$$$\sqrt{{f}\left({x}\right)}\:=\:{x}+\mathrm{2}\sqrt{{x}}\:+\mathrm{2}\: \\ $$$$\sqrt{{f}\left({x}\right)}\:=\:\left(\sqrt{{x}}\right)^{\mathrm{2}} \:+\:\mathrm{2}\sqrt{{x}}\:+\mathrm{2}\: \\ $$$$\sqrt{{f}\left({x}\right)}\:=\:\left(\sqrt{{x}}\:+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{1}\: \\ $$$${f}\left({x}\right)\:=\:\left\{\:\left(\sqrt{{x}}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}\right\}^{\mathrm{2}} \\ $$

Answered by Dwaipayan Shikari last updated on 12/Aug/20

lim_(x→0) ((sin(πcos^2 x))/x^2 )=((sin(π−πsin^2 x))/x^2 )=((sinπcos(πsin^2 x)−cosπsin(πsin^2 x))/x^2 ) =((sin(πsin^2 x))/x^2 )=((sin(πx^2 ))/x^2 )=((πx^2 )/x^2 )=π (sin(πsin^2 x)→sin(πx^2 )) (sin(πx^2 )→πx^2 )

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{sin}\left(\pi{cos}^{\mathrm{2}} {x}\right)}{{x}^{\mathrm{2}} }=\frac{{sin}\left(\pi−\pi{sin}^{\mathrm{2}} {x}\right)}{{x}^{\mathrm{2}} }=\frac{{sin}\pi{cos}\left(\pi{sin}^{\mathrm{2}} {x}\right)−{cos}\pi{sin}\left(\pi{sin}^{\mathrm{2}} {x}\right)}{{x}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{{sin}\left(\pi{sin}^{\mathrm{2}} {x}\right)}{{x}^{\mathrm{2}} }=\frac{{sin}\left(\pi{x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} }=\frac{\pi{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} }=\pi\:\:\:\:\:\left({sin}\left(\pi{sin}^{\mathrm{2}} {x}\right)\rightarrow{sin}\left(\pi{x}^{\mathrm{2}} \right)\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({sin}\left(\pi{x}^{\mathrm{2}} \right)\rightarrow\pi{x}^{\mathrm{2}} \right) \\ $$

Answered by Dwaipayan Shikari last updated on 12/Aug/20

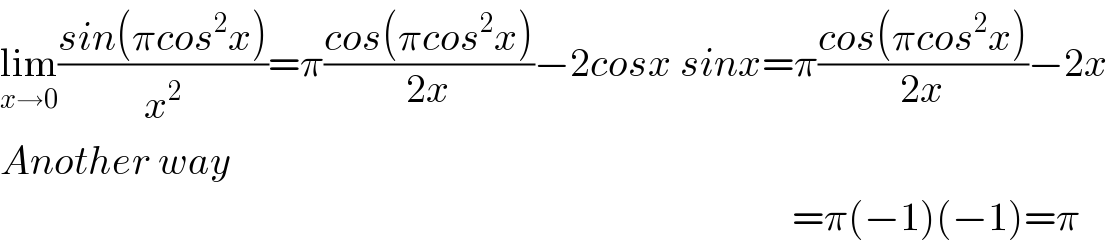
lim_(x→0) ((sin(πcos^2 x))/x^2 )=π((cos(πcos^2 x))/(2x))−2cosx sinx=π((cos(πcos^2 x))/(2x))−2x Another way =π(−1)(−1)=π

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{sin}\left(\pi{cos}^{\mathrm{2}} {x}\right)}{{x}^{\mathrm{2}} }=\pi\frac{{cos}\left(\pi{cos}^{\mathrm{2}} {x}\right)}{\mathrm{2}{x}}−\mathrm{2}{cosx}\:{sinx}=\pi\frac{{cos}\left(\pi{cos}^{\mathrm{2}} {x}\right)}{\mathrm{2}{x}}−\mathrm{2}{x} \\ $$$${Another}\:{way} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\pi\left(−\mathrm{1}\right)\left(−\mathrm{1}\right)=\pi \\ $$

Answered by john santu last updated on 12/Aug/20

((♣JS♣)/…) (1) ∫ _0 ^∞ ((√x)/(1+x^3 )) dx [ let h=(√(x )) ] ∫_0 ^∞ (h/(1+h^6 )) .(2h)dh = ∫_0 ^∞ ((2h^2 )/(1+h^6 )) dh now set q=h^3 ; ∫_0 ^∞ (2/(1+q^3 )) .(1/3)dq = [(2/3) arc tan q ]_0 ^∞ = (2/3)×(π/2)= = (π/3)

$$\:\:\:\:\:\:\:\frac{\clubsuit\mathcal{JS}\clubsuit}{\ldots} \\ $$$$\left(\mathrm{1}\right)\:\int\overset{\infty} {\:}_{\mathrm{0}} \frac{\sqrt{{x}}}{\mathrm{1}+{x}^{\mathrm{3}} }\:{dx}\:\:\left[\:{let}\:{h}=\sqrt{{x}\:}\:\right] \\ $$$$\underset{\mathrm{0}} {\overset{\infty} {\int}}\:\frac{{h}}{\mathrm{1}+{h}^{\mathrm{6}} }\:.\left(\mathrm{2}{h}\right){dh}\:=\:\underset{\mathrm{0}} {\overset{\infty} {\int}}\:\frac{\mathrm{2}{h}^{\mathrm{2}} }{\mathrm{1}+{h}^{\mathrm{6}} }\:{dh} \\ $$$${now}\:{set}\:{q}={h}^{\mathrm{3}} ;\: \\ $$$$\underset{\mathrm{0}} {\overset{\infty} {\int}}\:\frac{\mathrm{2}}{\mathrm{1}+{q}^{\mathrm{3}} }\:.\frac{\mathrm{1}}{\mathrm{3}}{dq}\:=\:\left[\frac{\mathrm{2}}{\mathrm{3}}\:\mathrm{arc}\:\mathrm{tan}\:{q}\:\right]_{\mathrm{0}} ^{\infty} \\ $$$$=\:\frac{\mathrm{2}}{\mathrm{3}}×\frac{\pi}{\mathrm{2}}=\:=\:\frac{\pi}{\mathrm{3}}\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com