Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 107794 by udaythool last updated on 12/Aug/20

Answered by arcana last updated on 12/Aug/20

Considere f(x)=x(√(1−x^2 )) ⇒f ′(x)=(√(1−x^2 ))−(x^2 /( (√(1−x^2 ))))=0, luego 1−2x^2 =0⇒x=(1/( (√2))). Decimos que (1/(√2),f(1/(√2))) es punto maximo de f. Por tanto, f(x)≤f(1/(√2)). Como ∣z∣=x^2 +y^2 ≤1, entonces xy≤x(√(1−x^2 ))≤1/2.

$$\mathrm{Considere} \\ $$$${f}\left({x}\right)={x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$$\Rightarrow{f}\:'\left({x}\right)=\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }−\frac{{x}^{\mathrm{2}} }{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}=\mathrm{0}, \\ $$$$\mathrm{luego}\:\mathrm{1}−\mathrm{2}{x}^{\mathrm{2}} =\mathrm{0}\Rightarrow{x}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}. \\ $$$$\mathrm{Decimos}\:\mathrm{que}\:\left(\mathrm{1}/\sqrt{\mathrm{2}},{f}\left(\mathrm{1}/\sqrt{\mathrm{2}}\right)\right)\:\mathrm{es}\:\mathrm{punto} \\ $$$$\mathrm{maximo}\:\mathrm{de}\:{f}. \\ $$$$\mathrm{Por}\:\mathrm{tanto},\:{f}\left({x}\right)\leqslant{f}\left(\mathrm{1}/\sqrt{\mathrm{2}}\right). \\ $$$$\mathrm{Como}\:\mid{z}\mid={x}^{\mathrm{2}} +{y}^{\mathrm{2}} \leqslant\mathrm{1},\:\mathrm{entonces} \\ $$$${xy}\leqslant{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\leqslant\mathrm{1}/\mathrm{2}. \\ $$$$ \\ $$

Commented by udaythool last updated on 13/Aug/20

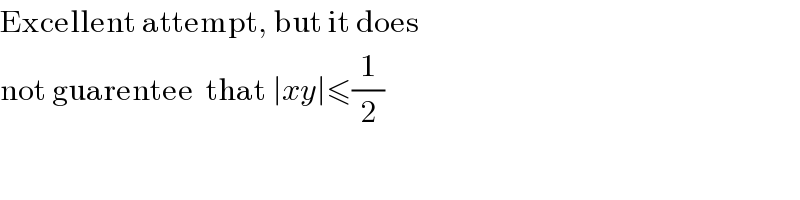
Excellent attempt, but it does not guarentee that ∣xy∣≤(1/2)

$$\mathrm{Excellent}\:\mathrm{attempt},\:\mathrm{but}\:\mathrm{it}\:\mathrm{does} \\ $$$$\mathrm{not}\:\mathrm{guarentee}\:\:\mathrm{that}\:\mid{xy}\mid\leqslant\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Commented by udaythool last updated on 14/Aug/20

I think by contradiction method we can prove it easily; Suppose ∀z=x+iy∈A, ∣xy∣≰(1/2) ⇒∃ some z=x+iy ∈A such that (1/2)<∣xy∣ But x^2 +y^2 ≤1 hence 0≥x^2 +y^2 −1>((1/(2y))−y)^2 ≥0 which is absurd...

$$\mathrm{I}\:\mathrm{think}\:\mathrm{by}\:\mathrm{contradiction}\:\mathrm{method} \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{prove}\:\mathrm{it}\:\mathrm{easily}; \\ $$$$\mathrm{Suppose}\:\forall{z}={x}+{iy}\in{A},\:\mid{xy}\mid\nleqslant\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\exists\:\mathrm{some}\:{z}={x}+{iy}\:\in{A}\:\mathrm{such}\:\mathrm{that} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}<\mid{xy}\mid \\ $$$$\mathrm{But}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \leqslant\mathrm{1}\:\mathrm{hence} \\ $$$$\mathrm{0}\geqslant{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{1}>\left(\frac{\mathrm{1}}{\mathrm{2}{y}}−{y}\right)^{\mathrm{2}} \geqslant\mathrm{0} \\ $$$$\mathrm{which}\:\mathrm{is}\:\mathrm{absurd}... \\ $$

Answered by mr W last updated on 12/Aug/20

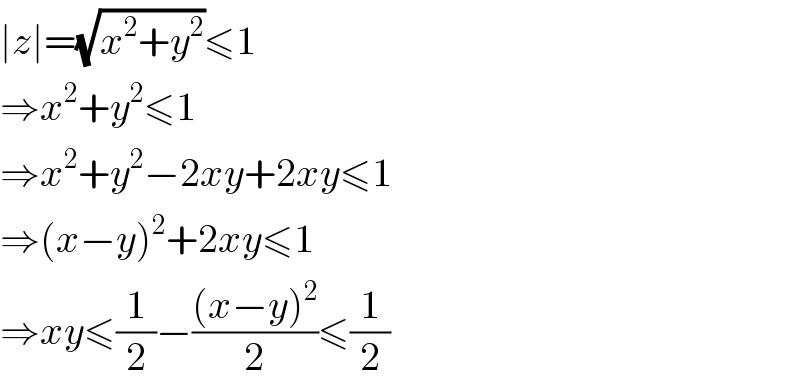
∣z∣=(√(x^2 +y^2 ))≤1 ⇒x^2 +y^2 ≤1 ⇒x^2 +y^2 −2xy+2xy≤1 ⇒(x−y)^2 +2xy≤1 ⇒xy≤(1/2)−(((x−y)^2 )/2)≤(1/2)

$$\mid{z}\mid=\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\leqslant\mathrm{1} \\ $$$$\Rightarrow{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \leqslant\mathrm{1} \\ $$$$\Rightarrow{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{2}{xy}+\mathrm{2}{xy}\leqslant\mathrm{1} \\ $$$$\Rightarrow\left({x}−{y}\right)^{\mathrm{2}} +\mathrm{2}{xy}\leqslant\mathrm{1} \\ $$$$\Rightarrow{xy}\leqslant\frac{\mathrm{1}}{\mathrm{2}}−\frac{\left({x}−{y}\right)^{\mathrm{2}} }{\mathrm{2}}\leqslant\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com